电路的均方根输出在宽范围内与温度呈线性比例关系

众所周知，p-n结二极管是最高约200℃的低温精密温度计的基础。流经二极管的电流保持恒定，二极管上的电压则提供了温度指示。恒定电流的幅值通常选小的，以便最大限度地减少二极管的自热效应。二极管电压随温度降低呈线性下降，因此有必要使用运放调节电路实现直接读数。输出校准使用电压基准实现。 在这个设计想法中，以恒定电流驱动的p-n结二极管概念是推导出来的，基本上取消了电压基准和运放。最终可以形成一个简单但高度精确的与温度呈比例的独特电路实现。本文还推荐了一些有趣的应用。电路的工作基于开关机制，允许两个交替的恒定电流流经二极管。这种方法用数学方法很容易理解，不过本文省略了一些细节。首先来看肖特基二极管公式：

9Veednc

上述公式给出了流经p-n结二极管的电流(I)与二极管上的电压(V)、温度(T)和二极管半导体材料的理想因子(n)之间的关系。k是波兹曼常数，q是电量。I_n项是二极管反向饱和电流中与温度无关的部分。在报道的实验[1]中，一个硅1N4148二极管由电流I₁和恒流I₂先后交替驱动，过渡发生在温度T点。 图1显示了两个电流对二极管电压的影响，其中二极管在恒温水槽中从温度T₀开始冷却。理论上，AB和CD线段向后延伸可以达到绝对零度(-273℃)。然而，二极管中的杂质和其它效应限制了电路只能工作到-200℃左右。

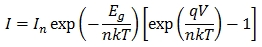
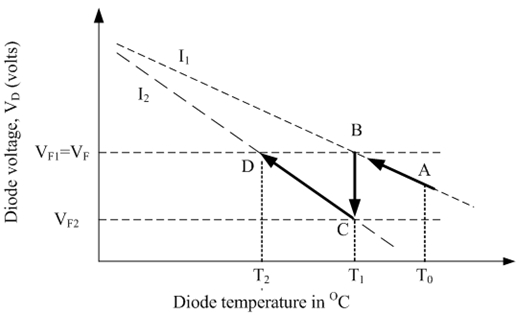
图1：直接均方根读数温度计的工作原理。
9Veednc

在温度T点，两个依次开关的电流的使用将产生数据对：(T, I₁, V₁)和(T, I₂, V₂)。将这对数据置入肖特基公式可以很容易发现理想因子项中的压差ΔV=V₁(T)-V₂(T)：

9Veednc

给定二极管的理想因子一般是常数，1N4148二极管的理想因子为1.9[1]。据观察，硅二极管的电路可预测性要好于锗二极管。在上个公式中，n、q/kT和ln(I₁/I₂)这几项都是常数，我们可以用一个新的常数b将这个公式改写为： ΔV(T)=bT，其中T的单位是开尔文 因此只要在测量温度点电流按比例开关，给定温度T点的电压差就直接正比于温度。开关切换时间要小于温度可能改变的时间。为了获得更高的测量精度，在感兴趣的温度点的电压差ΔV要大。图1就建议大的I₁/I₂比值，但如果I₁太大的话，自身产热会上升。图2显示了一种创新的开关型恒流镜像电路，该电路由晶体管Q₁和Q₂组成，其中输出电流在D₁中进行了镜像。

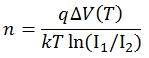
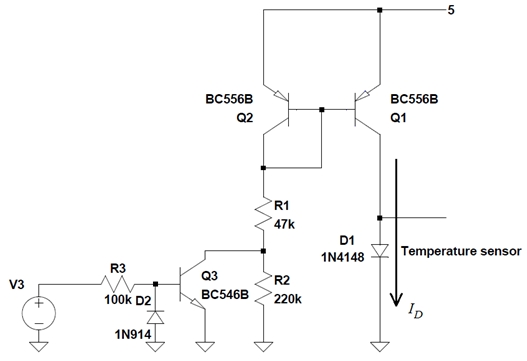
图2：开关型恒流源。
9Veednc

在图2中，Q₂的负载电阻通过额外晶体管Q₃切入或切出集电极，而Q₃则由50%占空比的时钟源V₃进行驱动。这样负载电阻就是可变的，当V₃=5V时负载电阻值为R₁，当V₃=0V时值为(R₁+R₂)。图2中显示的值给出了20.14μA或111.38μA这两个镜像电流。将所有常数代入压差公式得到： ΔV(T)=2.8×10^-4T 根据这个公式可以预测，温度在-200℃时输出ΔV=20.5mV，25℃时为83.4mV，200℃时为132.0mV。使用运放的放大电路可以将输出提升到要求的水平。 在最终电路中，时钟源可以是接近50%占空比的555非稳态时钟，或嵌入式控制器的PWM输出。设计在10kHz处进行了测试。二极管电压在V₁和V₂之间切换，因此固有直流电平可以使用具有低截止频率(比如2Hz)的简单RC网络进行滤除。 滤波可以确保方波输出，并且可以忽略峰值电平衰减，不会引入频率相关性。输出随后可以用交流模式的真正均方根数字电压表在图3中的“out1”端读出。

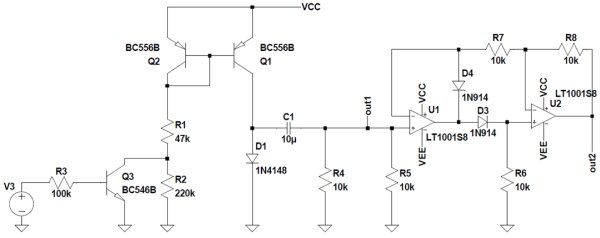
图3：均方根输出直接正比于温度的功能性电路。
9Veednc

工作频率上限是二极管开关响应变得迟缓时的值。可以实现多种读数增强功能。例如，将单位增益检波器或精密全波整流器[2]连接到滤波器输出端，确保输出是正的，并且在图3中的“out2”处得到与温度呈比例的峰值和均方根值。 这种电路的可能应用有直接读数的超线性宽范围温度计、闭环温度控制以及温度数据采集。将滤波后的输出波形对高频载波进行幅度调制是一种有趣的应用。如果去掉RC滤波器、二极管直流中心电压先缓冲然后应用到线性VCO中的调谐变容二极管还可以实现温度对频率的调制。频率偏差则直接正比于温度。 参考文献 [1] R O Ocaya and P V C Luhanga 2011 Eur. J. Phys. 32 1155 doi:10.1088/0143-0807/32/5/003 [2] Jones D and Stitt, Precision Absolute Value circuits, SBOA068, Burr-Brown 原文作者：R O Ocaya 《电子技术设计》网站版权所有，谢绝转载