
曾几何时(2017年),我发布了一个简单的设计实例“Cancel PWM DAC ripple with analog subtraction”,用于将PWM DAC输出纹波滤除和衰减——十多年来我发现它非常有用。
其原理是将PWM信号与其交流耦合的反相信号进行无源求和,为的是在不影响直流分量的情况下将不期望的交流纹波信号分量衰减掉(图1)。
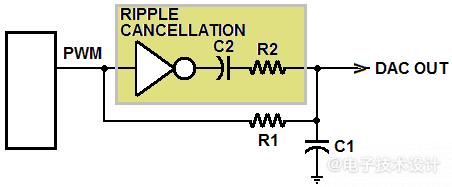
图1:原始纹波减法拓扑。
然而,有关这个实例运作的一些细节,我并没有在最初的短文中进行充分探讨。下文介绍了一些被省略的内容。
该电路的基本工作原理是将交流耦合(通过C2)的反相PWM纹波信号电流与PWM信号电流进行无源求和(通过R1和R2),然后在DAC输出电容器C1中对该总和进行积分。由此产生的纹波分量的部分抵消,可实现足够的纹波衰减,同时所使用的滤波器时间常数也比采用单级RC滤波器所需的时间常数短得多。更快的响应过程和更短的稳定时间是回报。
然而,这种电流模式方案有个缺点会限制其速度,即在PWM输入占空比发生阶跃变化后,R1和R2电流符号会立即变反但幅度相等,因此其和一定暂时为零。因此,由于C1没有电流积分,DAC输出信号无法开始对阶跃进行响应,直到C2开始充电,使通过R2的电流减少,从而使R1和R2电流不相等,并为C1提供除零以外的值进行积分。这种不期望的空值间隔在图2中表现为输出波形上升沿中有明显的时间延迟。
这种对DAC响应时间的限制似乎是电流模式求和拓扑所不可避免的缺点。虽然它仍然比单级RC滤波器快(很多),但可能没有它可以/应该的那么快。
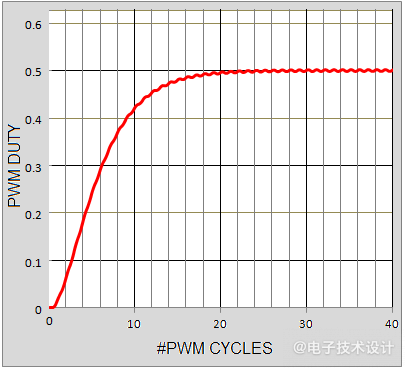
图2:电流模式纹波减法响应有前沿延迟。
因此,我开始感到疑惑。如果首先计算纹波和PWM电压而不是电流,然后相互减去,实现纹波抵消,会发生什么情况?能否从最初的实例中榨取更多的性能,同时又不失去最初使它具有吸引力的简单性呢?图3的拓扑就是答案。
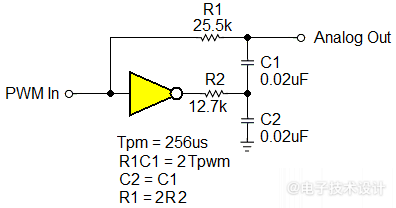
图3:新型电压模式纹波减法电路。
新电路的运行依赖于串联的电容器C1(用于产生PWM直流电压分量)和C2(用于提供反相纹波分量)。电压总和是串联电容器连接所固有的,因此,与2017年的电路一样,可以从直流输出中减去交流纹波。事实证明,如果R1C1时间常数刚好等于2Tpwm,即PWM周期的两倍——在本例,也即具有1MHz时钟的8位PWM中仅为512µs——则纹波衰减足以满足8位分辨率。更快的时钟当然可以实现更短的时间常数。
请注意,新滤波电路的总元件数与原来的完全相同:一个反相器(例如1/6 SN74HC04)、两个电阻器和两个电容器。
图4显示,与图2的电流模式求和延迟不同,其阶跃响应现在立即在T=0时开始,对于此Tpwm将在16个PWM周期≈4ms内实现8位稳定。
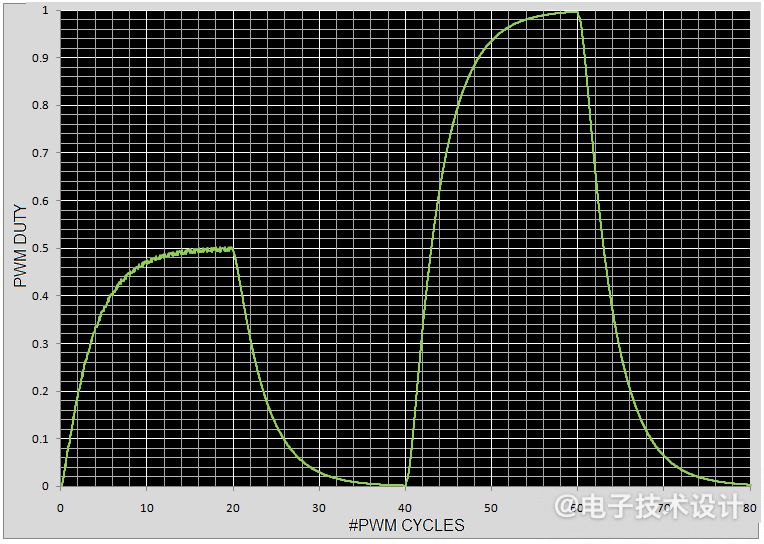
图4:电压模式阶跃响应无前沿延迟。
图5比较了原始电流模式设计(约23Tpwm)与新电压模式版本(约16Tpwm)的8位阶跃稳定时间。
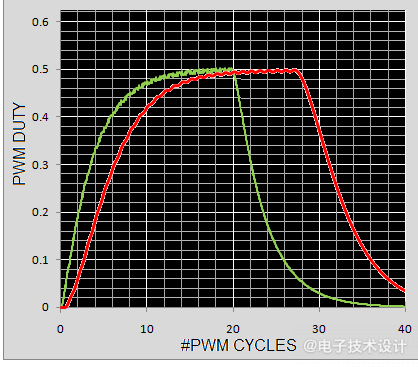
图5:电流模式(红色)与电压模式(绿色)响应的比较。
响应速度提高了44%(23/16),似乎是值得的性能改进,特别是考虑到相关的电路复杂性和成本并未增加。
适用于原始电流模式拓扑的详细说明(例如,利用更快的时钟速率、精密模拟开关和电压参考来提高精度、噪声和准确度),当然也直接适用于这个新的电压模式版本。
(原文刊登于EDN美国版,参考链接:Cancel PWM DAC ripple with analog subtraction—revisited,由Franklin Zhao编译。)
本文为《电子技术设计》2023年4月刊杂志文章,版权所有,禁止转载。免费杂志订阅申请点击这里。
 最前沿的电子设计资讯
最前沿的电子设计资讯