
数制是用于表示数字和数值的符号集。它具有计算和执行许多数学运算的方法和规则。在我们的数字电子课程的第3部分中,将深入研究这个概念,因为它是应用于数字电子的所有方法的基础。
执行算术和数学计算是一种在进制中更容易的操作。后者使用一定数量的数字(或符号)构成数制的基础(见图1)。10进制系统由10个符号组成,8进制系统由8个符号组成,2进制系统仅由2个符号组成。所考虑的实体的最终值取决于所使用的符号数量和每个符号所占据的位置。目前先进的文明使用的数制是以10为基数(十进制)并使用十位数字(0、1、2、3、4、5、6、7、8、9)。为方便起见,人类正是使用这种以十为基数的系统,因为手上有十根手指,他可以轻松计算出数学值。如果他有六个手指,他可能会使用基数为6的系统。基数越小,表示相同数字所需的位数就越多,反之亦然。例如,为了表示数字2023,以下各种基数的表示方法都是有效和等价的:
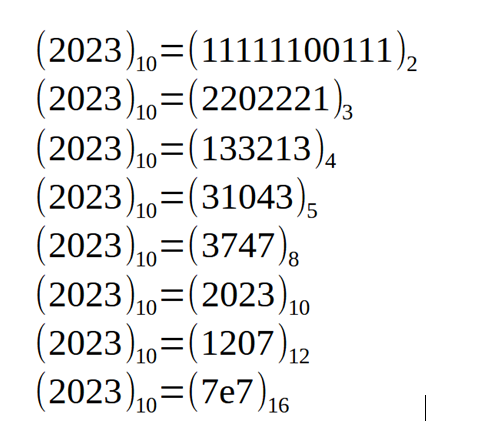
因此,二进制系统比十进制系统需要更多的数字,反过来,十进制系统比十六进制系统需要更多的数字,表示的也是相同的值。因此,数制基数的选择是非常常规的。使用的符号也是一种惯例,理论上,任何人都可以使用自己的一组数字和符号来创建自己的数制来适应他们。
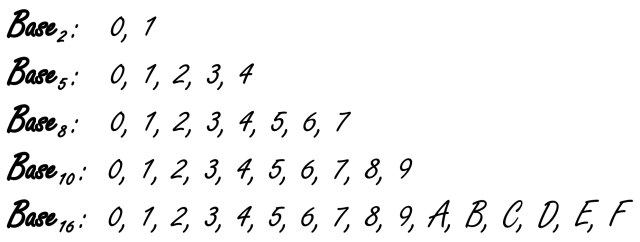
图1:被使用的一些数制和符号
所有数制,无论以何种基数,都是极其重要的,但在本文中,我们将深入研究以2为基数的数制,这是当今电子系统首选的数制,因为逻辑和电气状态的数量恰好是2(开和关)。
今天,二进制系统随处可见,只有两种状态,它也可以再现复杂的元素。它具有相当大的优势。今天的计算机,无论它们多么强大,都使用相当过时的逻辑规则来执行各种程序。这一切的根源是二进制运算。在二进制(或基数为2)的数制中,只有0和1这两个数字。如果一个数字向左移动一个位置,则该值就会乘以2。相反,如果一个数字向右移动一个位置,该值除以2。下面的例子很好地说明了此问题。假设我们有以10为基数的值8,对应于以2为基数的值00001000。您还可以用以下方式说明这个等价关系:
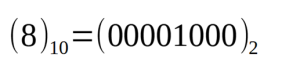
由于在十进制系统中,所有放在左边的零都没有值,因此二进制数也可以表示为:
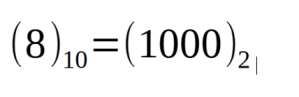
如前所述,乘以2是通过将整个值块向左移动一位来执行的,如下例所示:
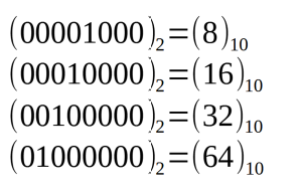
另一方面,除以2是通过将整个值块向右移动一个位置来完成的,如下例所示:
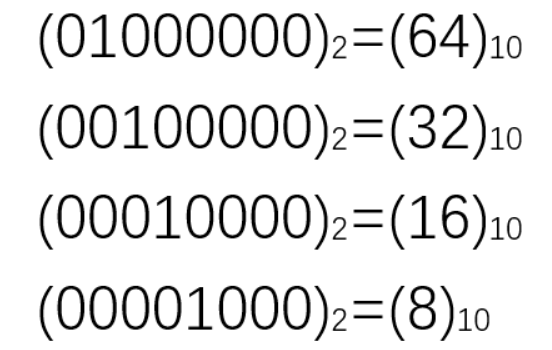
计算数字的方式与十进制系统相同:使用第一位数字,列出所有符号0和1,然后使用第二位数字,从左侧的1开始,并在右侧重复数字0到1。当所有的组合都完成后,在考虑三位数。以此类推继续计数。下面的例子更好地阐明了计数顺序的概念。
| Dec | Bin | Dec | Bin | Dec | Bin | Dec | Bin |
| 0 | 0 | 16 | 10000 | 32 | 100000 | 48 | 110000 |
| 1 | 1 | 17 | 10001 | 33 | 100001 | 49 | 110001 |
| 2 | 10 | 18 | 10010 | 34 | 100010 | 50 | 110010 |
| 3 | 11 | 19 | 10011 | 35 | 100011 | 51 | 110011 |
| 4 | 100 | 20 | 10100 | 36 | 100100 | 52 | 110100 |
| 5 | 101 | 21 | 10101 | 37 | 100101 | 53 | 110101 |
| 6 | 110 | 22 | 10110 | 38 | 100110 | 54 | 110110 |
| 7 | 111 | 23 | 10111 | 39 | 100111 | 55 | 110111 |
| 8 | 1000 | 24 | 11000 | 40 | 101000 | 56 | 111000 |
| 9 | 1001 | 25 | 11001 | 41 | 101001 | 57 | 111001 |
| 10 | 1010 | 26 | 11010 | 42 | 101010 | 58 | 111010 |
| 11 | 1011 | 27 | 11011 | 43 | 101011 | 59 | 111011 |
| 12 | 1100 | 28 | 11100 | 44 | 101100 | 60 | 111100 |
| 13 | 1101 | 29 | 11101 | 45 | 101101 | 61 | 111101 |
| 14 | 1110 | 30 | 11110 | 46 | 101110 | 62 | 111110 |
| 15 | 1111 | 31 | 11111 | 47 | 101111 | 63 | 111111 |
在进制系统中,如前所述,每次向左侧移动位置时所表示的数字要乘以基数,每次向右侧移动时始终除以基数。很明显,如果你想把这个数提升到3次方,比如你只需要向左走3次就可以了。在十进制系统中也会发生同样的情况。位置左移相当于该值乘以10,位置右移相当于相同值除以10。下面是一些解释性的例子。尽管到目前为止,所有设备(PC、智能手机、平板电脑)都拥有科学计算器(参见图2中的Windows计算器),用它可以进行任何进制的所有运算,也可以进行一个进制和另一个进制之间的转换,但了解最重要的计算方法总是有用的。
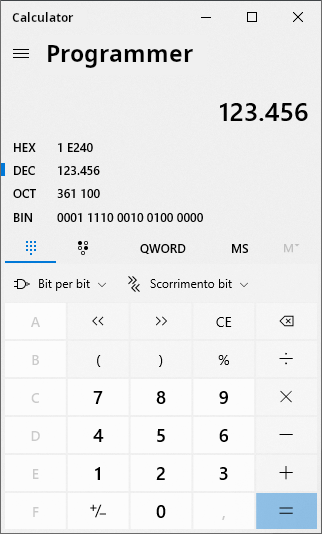
图2:编程模式下的Windows计算器
求和无疑是最简单的算术运算,与十进制非常相似。它基于以下单个二进制数字的总和:

有了这个经验法则,再加上一点耐心和注意力,就可以执行任何类型、任何难度的加法。

使用简单的操作,可以将数字从一个进制转换为另一个进制中的相应表示。下面我们来研究一下二进制数到十进制数的转换。例如,让我们有以下要转换的值:
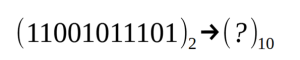
从左边开始,将单个二进制数字(1或0)乘以2的次方,直至该数字所占位置的数字减一。最右边的位置是0,而最左边的位置等于位数减一。
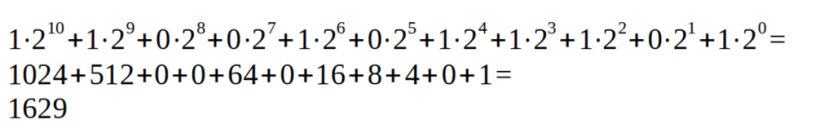
所以:
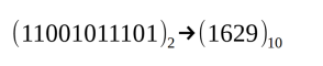
另一种更快更友好的方法如下。我们将各个符号写在表格的一行上。在顶行,计算2的幂,从右边开始,向左加倍。最后,将等于1的符号(绿色背景)处的2的幂相加。最后的表格如下所示。

将1024+512+64+16+8+4+1相加得到以10为基数的值1629。相反的转换,即将数值从十进制系统转换为二进制系统,是以一种不同但同样简单的方式进行的。转换过程涉及一系列连续除以2。每个除法的余数仅代表二进制数的一个数字(0或1),从右到左。此外,每次除法的结果成为下一次除法的被除数。当结果等于0时转换停止,即当没有更多的除法要执行时。例如,让我们有以下要转换的值:
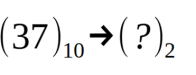
连续划分的过程如下:

从下到上,十进制数37对应的二进制数是100101,按照下面的表示法:
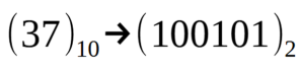
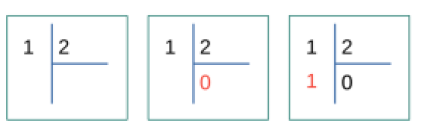
可能会出现一个问题。为什么最后一次除法时,1:2除法的余数等于1?下面的图示将我们带回到幼儿园,澄清了所有疑问。
下面,我们提出两种简单的算法来执行数制之间的转换。它们非常简单,并且是用标准C语言编写的。显然,它们并不构成一个放之四海而皆准的解决方案,但软件可以用无数种不同的方式编写。第一种是将一个数字从二进制系统转换到十进制系统。第二种执行相反的操作,将一个数字从十进制系统转换到二进制系统。
#include <stdio.h>
void main()
{
long num, binary_num, decimal_num = 0, base = 1, rem;
printf (” Enter a binary number \n”);
scanf (” %ld”, &num);
binary_num = num;
while ( num > 0)
{
rem = num % 10;
decimal_num = decimal_num + rem * base;
num = num / 10;
base = base * 2;
}
printf ( ” The binary number is %ld \t”, binary_num);
printf (” \n The decimal number is %d \t”, decimal_num);
}
#include <stdio.h>
void main() {
int n, c, k;
printf(“Enter a number in base 10\n”);
scanf(“%d”, &n);
printf(“%d in binary number system is:\n”, n);
for (c = 10; c >= 0; c–) {
k = n >> c;
if (k & 1)
printf(“1”);
else
printf(“0”);
}
printf(“\n”);
}
所有数制的原理都是一样的;仅使用的符号数量发生变化。此外,所有系统也都是相似的;只有符号的数量发生变化。不要低估对二进制系统的理解和掌握,因为它将被大量用于电子器件、软件创建,尤其是微控制器编程中。
(原文刊登于EDN姊妹网站EEWeb,参考链接:Digital Electronics Course: Part 3 – Numbering Systems,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯