
正如在之前的文章中看到的那样,数字电子产品的信息只有两种可能状态:真和假。无论是电流、数字数据还是任何类型的变量,系统的最终选择都只取决于这些事实的真假。事实上,二进制电子电路也因此而得名。在本文中,我们将探讨数字电子电路的核心主题,即二进制值的布尔理论。
布尔代数(以数学家George Boole的名字命名)是数学的一个分支,包括二进制处理的理论和实践。它基于这样一个事实,即每个概念或每个句子都可以是真或假。这个数学分支关注的是将几个逻辑句子放在一起并验证它们的最终结论。可以通过组合更简单的命题来创建新的逻辑命题。下面显示了一些示例逻辑命题。
很明显,命题可以具有“逻辑真”(例如第一、第二、第三和第四命题)或“逻辑假”(例如第五命题)的特征。布尔代数不考察单个命题的逻辑值,而是着眼于将多个命题组合在一起,作为不同事实之间逻辑运算的结果,最终形成单一命题的可能性。例如,以下命题结合了几个条件并创建了一个新的、单一的逻辑最终命题,由AND(与)型的条件句处理:
在下一个示例中,以下命题结合了几个条件并创建了一个新的且唯一的逻辑最终命题,由OR(或)类型的条件句处理:
逻辑命题也可以通过NOT(非)条件句处理否定句,如下例所示:
因此,设计者可以通过简单地将结构和命题尽可能清晰和有效地结合起来,来创建任何类型的子句。在后面的课程中,我们还将了解如何优化逻辑表达式,以使其更短更简单。
真值表是用于确定两个或多个命题的结果是真还是假的简单表格。它们使计算表达式中考虑的命题的真值变得更容易。下面,我们列出了一些与逻辑运算符AND、OR和NOT相关的真值表。

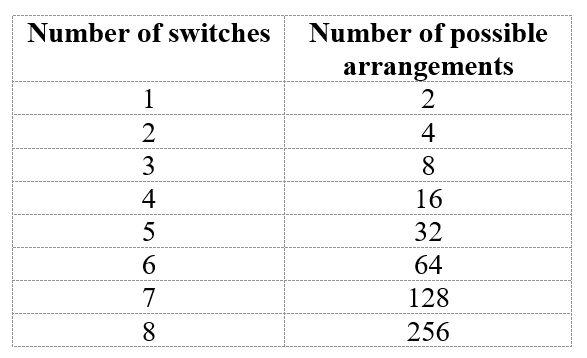
上表很容易阅读。两列(Input1和Input2)代表任何通用电路输入的逻辑状态。第三列“Output”表示相应输出的逻辑状态。使用逻辑运算符AND,只有当两个输入的逻辑级别都为真(1)时,输出才为真(1)。两个输入的所有组合生成四种可能的逻辑或电气场景。在这种情况下,两个命题的处理方式是,只有当两个命题都为真时,结果才为真。从图1的电路图中可以看出该表的实际应用,其中两个相互串联的开关必须点亮一个灯泡。很明显,这个灯泡只有在两个开关都闭合并且电流可以流过电路时才会点亮。换句话说,只有当第一个输入和第二个输入都为逻辑值真时,灯泡才会被打开。
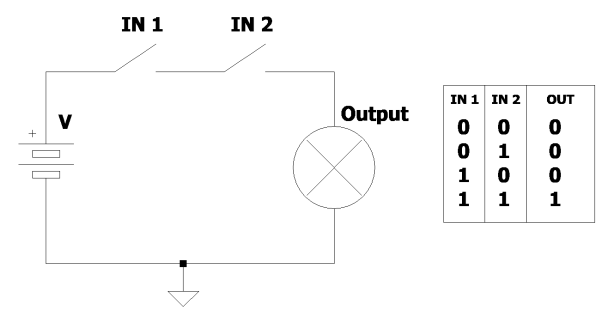
图1:两个开关和一个灯泡完美地仿真了两个逻辑命题和AND条件的操作。
有趣的是,根据下面的通用公式,AND类型的逻辑表达式也可以用各个命题之间的乘法来表示:
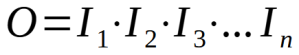
同样,当两个输入都为值1(1x1=1)时,电路的输出等于值1。

随着输入数量的增加,与输出的逻辑状态相关的最终组合的数量也会增加。例如,对于一个由三个输入和一个输出组成的真值表,就会发生这种情况,其电路图如图2所示。
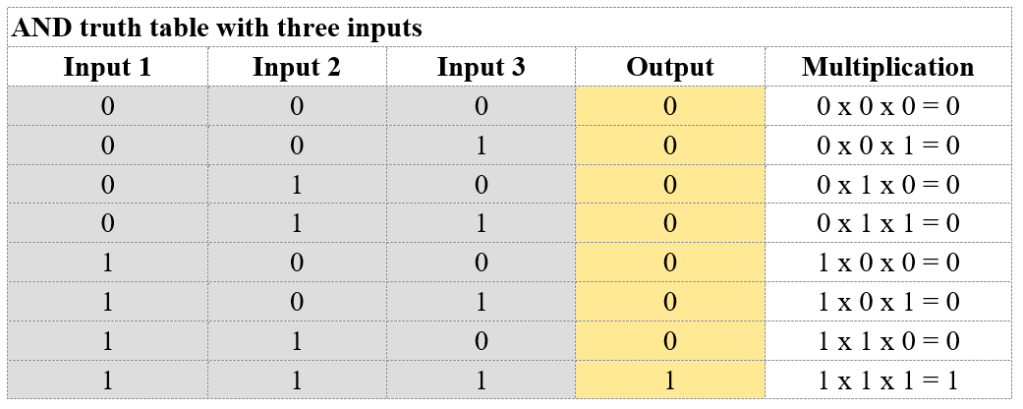
使用这种解决方案,灯泡只有在三个开关闭合时才会点亮,从而允许电流流过电路。三个输入的所有组合产生八种可能的逻辑或电气场景,只有当第一个输入、第二个输入和第三个输入同时取逻辑值真(1)时,灯泡才会打开。同样,AND类型的逻辑表达式可以使用各个命题之间的乘法来表示,如上表所示。第五列对于真值表的实际用途来说并非不可或缺,但很有用,它显示了如何使用各个逻辑命题值之间的简单乘法来计算AND值。三个开关,即三个逻辑输入,只有当三个输入都等于1时,电路的输出才等于逻辑值1(1×1=1)。
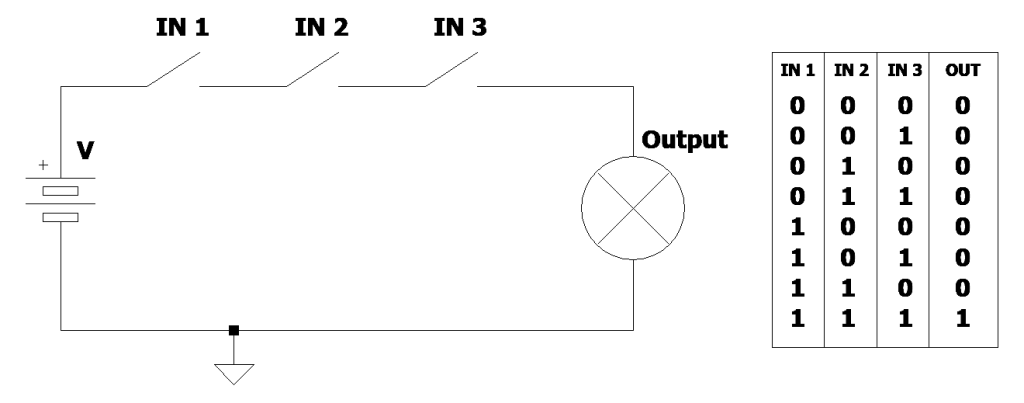
图2:三个开关和一个灯泡完美仿真了三个逻辑命题和AND条件的运行。
由于计算的对象是二进制值,即它们只能呈现两种不同的逻辑状态,因此通过组合开关的所有状态来计算存在多少个解决方案,可以简单地计算有"n"个不同元素的"k"类重复排列的数量,根据以下公式:
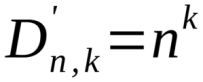
下表给出了使用不同开关重复排列的次数:
前面示例的规定要求所有开关都闭合,以使电流在电路中循环。如果只有一个开关打开,灯泡仍会关闭。逻辑运算符OR的真值表相对更柔和、更灵活,并提供以下仅两个开关的可能排列编码:

相关电路图如图3所示,显示了电压发生器、两个开关(这次彼此并联)以及电路输出端的灯泡的布置。在这种类型的配置中,如果两个开关中至少有一个闭合,则输出端的灯泡会打开。只有当两个开关都打开时,即如果相应的逻辑信号为0,灯泡才会关闭。
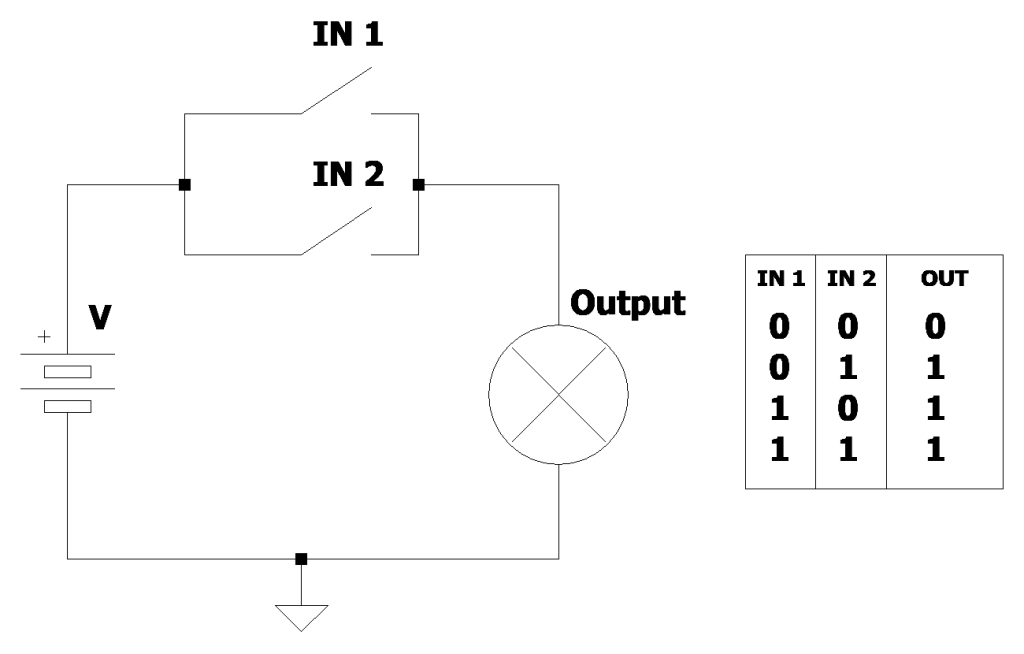
图3:两个开关和一个灯泡完美仿真了两个逻辑命题和OR条件的运行。
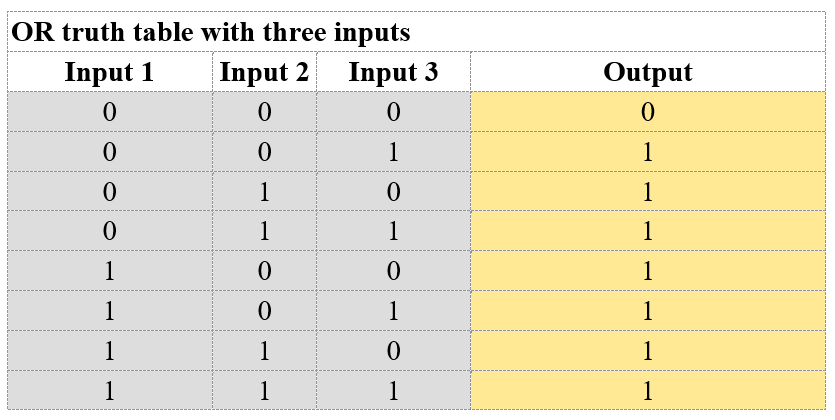
同样,通过增加输入的数量,与输出的逻辑状态相关的最终组合的数量也会增加。对于由三个输入和一个输出组成的真值表,最终场景如图4所示。总排列数遵循与之前相同的公式。
根据以下通用公式,OR类型的逻辑表达式也可以使用各个命题之间的加法来表示:
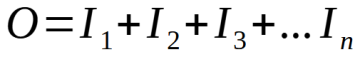
最终,重复排列的数量与AND解决方案相同。
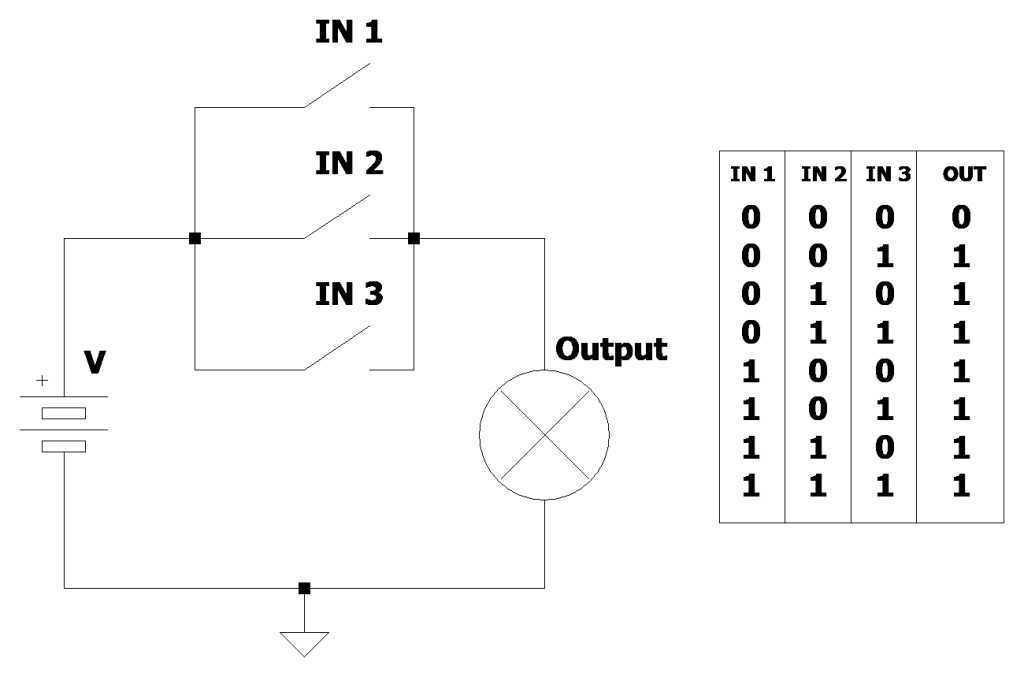
图4:三个开关和一个灯泡完美仿真了三个逻辑命题和OR条件的运算。
逻辑运算符NOT(一元)对应的真值表非常简单。它通过反转输入的逻辑状态来运行。如果输入为真,则输出为假,反之亦然。下面的真值表总结了它的简单操作。
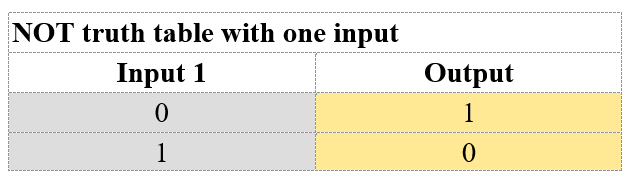
根据以下通用公式,NOT 类型的逻辑表达式也可以使用减法表示:

真值表不仅是一种数学和逻辑理论,而且在数字系统的设计中也非常有用。在任何编程语言中都有许多研究和不同的方法来使用这些表,尤其是在微控制器应用程序的应用方面。因此,我们邀请读者深入研究数字电子领域,这无疑将在任何类型的已开发的电子解决方案中具有广泛的实际应用。
(原文刊登于EDN姊妹网站EEWeb,参考链接:Digital Electronics Course – Part 4: Boolean Algebra and Boolean Functions,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯