
尽管MCU片上模拟外设的种类和数量在不断提高并且其成本也在不断下降,但很多工程师仍然喜欢采用PWM DAC这种简单设计,因为它可以获得“免费”的DAC。具体做法就是对未指定的DIO引脚和计数器/定时器模块进行重新利用,然后添加一个简单的低通滤波器来滤除纹波,这样就得到了一个虽然不完美但依然实用的模拟输出。
但是,这一数据转换信号链的反方向该怎么办呢?我们离零成本的(虽然不完美但依然实用的)ADC设计还有多远呢?图1就是我所设计的“免费”的ADC,其中仅使用了两个晶体管、四个电阻器和一个电容器,成本小于0.5美元。
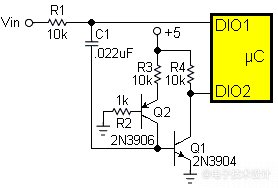
图1:近乎“免费”的ADC电路设计。
以下是它的工作原理。
当将三态I/O引脚DIO1编程为高阻态时,就可以让C1的顶端通过R1进行充电并对输入电压Vin进行采集,如图2的采集阶段所示。
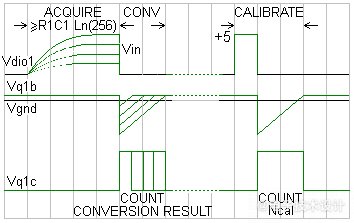
图2:“免费”ADC的采集、转换和校准阶段。
DIO1处于高阻态采集阶段的最短持续时间,将由N(所需的转换精度位数)和R1C1时间常数所决定。
最小采集间隔=R1C1·ln(2N)
例如,对于本文给定的RC值和N=8,最小间隔约为1.5ms。如果N=12,则最小间隔约为2ms。当向C1充电时,Q1的正向偏置状态和饱和基极,将提供大约1Ω的低阻抗接地路径,且其偏移量(Vq1b)约为650mV。采集阶段结束时,将DIO1重新编程为0输出。这就会将C1的顶端驱动至地,并将Vq1b驱动为负,从而使Q1关断。Q1关断即可让DIO2=1——之所以将该引脚编程成这样,就是为了让MCU计数器/定时器外设能开始对时钟周期(例如1MHz)进行计数——从而测量Q1关断的持续时间。
Q1关断期间将会持续计数,直到C1的负电荷消散而让Vq1b能够返回到650mV。该过程所经过的时间(也即计算的周期数)与Vin成正比,而与电流源Q2的集电极电流成反比:
C1放电间隔=C1·Vin/Iq2c
Iq2c=(5V–Vq2e)/R3·αq2≈430µA
因此可得以下近似值:
计数间隔=51µs·电压转换次数=51·fclk(MHz)·Vin
R2的作用是避免Q2发生饱和。R4是Q1的集电极和DIO2的上拉电阻。将采集时间(1.5ms)和转换时间(在8位和1MHz时钟的条件下为256µs)结合起来,即可预测最大转换速率约为560Sps。
但是,如何解决那个“近似值”的问题呢?这个电路要做到“免费”,就意味着它包含大量限制,例如廉价的电阻器、电容器和晶体管偏置电压和电流增益的温度系数,因此简单地忽略这个问题是行不通的。
幸运的是,如图2右侧所示,这个“免费”的ADC具有自校准功能。
为了实现自校准,需要将DIO1编程为输出,将其设置为1而为C1充电,然后设置为0以生成计数间隔和Ncal计数值。随后的转换结果将按比例缩放为:
Vin=5V·转换次数/Ncal
这样就纠正了上述大多数误差来源。但不幸的是,并非全部。
由于将Q1关断而生成非零计数间隔有最小Vq1b偏移量的要求,剩下的一个误差来源就是未校准的零偏移。这样做所需最小的Vin约为10mV,对于满量程5V、8位转换结果的情况也即0.01/5=1/500≈1/2LSB。
这样就只留下一个明显潜在不准确的来源:5V电源。逻辑电源对模拟参考来说并不是最佳选择,因此这种“免费”ADC的精度最终将取决于实际所用电源的好坏。
当然,经典的PWM DAC也会有完全相同的逻辑电源限制问题,但这并没有否定它的实用性或受欢迎程度。
这就有点将这个“免费”模拟外设的主题带回到了它开始的地方——虽然不完美但依然实用?
(原文刊登于EDN美国版,参考链接:A "free" ADC,由Franklin Zhao编译。)
本文为《电子技术设计》2023年5月刊杂志文章,版权所有,禁止转载。免费杂志订阅申请点击这里。
 最前沿的电子设计资讯
最前沿的电子设计资讯