
这本关于电力电子的笔记的结构如下:
阅读这些教程的需要电气工程的基础知识。
让我们仔细考虑一下图1所示的简单电路,它由一个二极管组成。应用三种不同类型的输入波形(正弦波、方波和锯齿波),要求我们确定哪种情况下电流将具有与输入信号相同的形状,分别检查正向和反向极化情况。
考虑图1,vin是三种可能的输入波形之一。更准确地说,vin(t)是周期τ=2π/ω的周期函数。
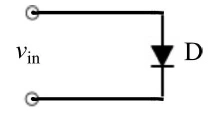
图1:只有一个二极管的简单电路
以下条件决定了二极管的正向和反向极化:

此外,二极管的电压-电流特性由下式给出:

由于VT值较低(在室温下约为26mV),即使输入电压为几伏,流过二极管的电流也会达到很高的值。我们将在仿真中使用50mV的输入信号峰值。
应用正弦输入并对i0上的电流进行归一化,我们有:

从等式(3)中,我们可以获得图2中所示的曲线图。在这里,我们可以看到电流虽然几乎是单向的,但并不具有正弦形状。
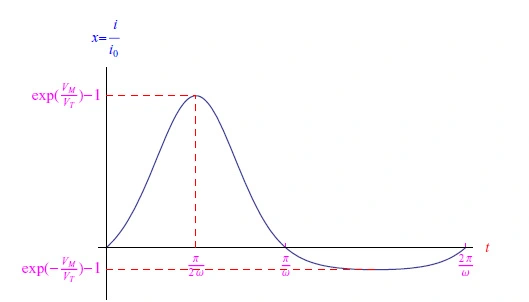
图2:正弦输入的二极管电流(归一化为i0)
电流具有图3所示的典型趋势,可以很容易地从电压-电流特性中计算出来:
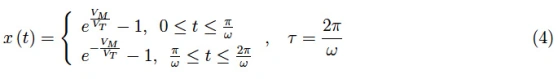
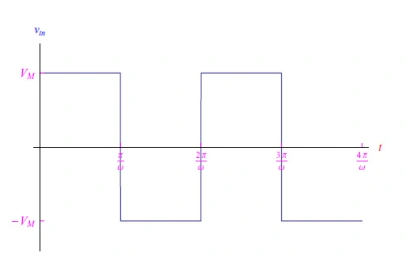
图3:幅度为VM的方波
结果,我们得到了图4所示的图形。
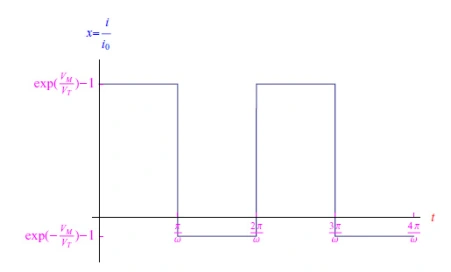
图4:输入信号为方波时二极管中的电流
以下等式给出了输入信号:
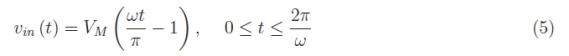
周期为2π/ω,相关曲线如图5所示。
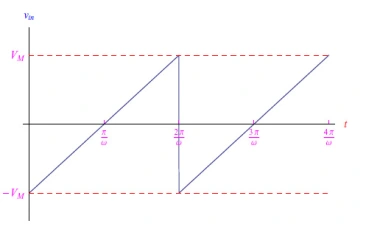
图5:幅度VM的锯齿波输入信号
流经二极管的归一化电流与输入信号具有相同的周期,由下式给出:
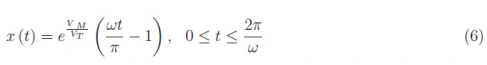
相应的图如图6所示。
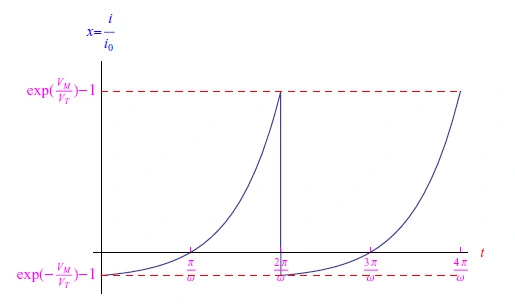
图6:当输入信号为锯齿波时二极管中的电流
因此,我们可以得出结论,唯一保留的波形是方波(即使它在纵坐标轴上被平移)。
为了分析反极性情况,我们将参考图7中所示的方案。
现在,二极管的正向和反向极化发生在:

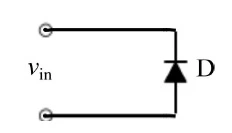
图7:反极性电路
为了得到电压-电流特性,我们必须改变等式(2)中指数参数的符号:

在正弦输入电压的情况下,我们有:
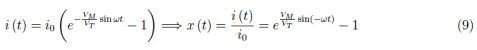
这里,我们假设三角正弦函数是奇函数。很容易相信x(t)的图形可以从与直线x=π/ω对称的直接极化图形中获得(图8)。鉴于二极管的极化状态是反转的,图表的这种“反转”趋势应该不足为奇。
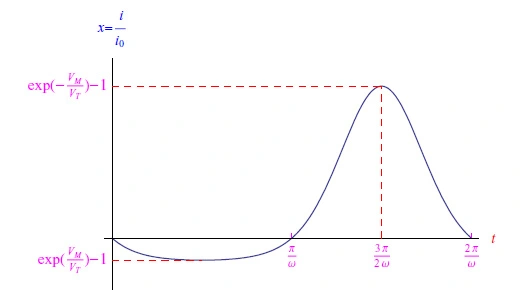
图8:二极管的电流(归一化为i0)用于反极性正弦输入
这一次,假设我们被要求证明以下说法的正确性,该说法粗略地描述了二极管的电路行为:“二极管在正向极化时为短路,在反向极化时为开路”。
我们可以尝试计算二极管的电阻,假设两端的电压降已知。但是,我们必须注意,因为与其他元件(电阻、电容和电感)不同,二极管不表现出线性行为。例如,对于电阻,其大小(电阻)可以定义如下:

其中v是电压降,i是电流强度。对于给定的电阻,R是一个常数。如果我们修改v的值,则当前i会更改以保持R的相同值。然而,在二极管的情况下,这个比率取决于v。为了在操作上定义类似于欧姆电阻的量,我们可以从电压-电流特性中获得电压v。之后,我们可以计算出这个函数的导数:

因此,我们定义了二极管的微分电阻。由式(11)可知,r随正向偏压压降v呈指数下降,随反向极化中|v|的增加而呈指数级上升。这证明了文本的主张。图9显示了室温下反向饱和电流为5µA的二极管的r与v的函数关系图。
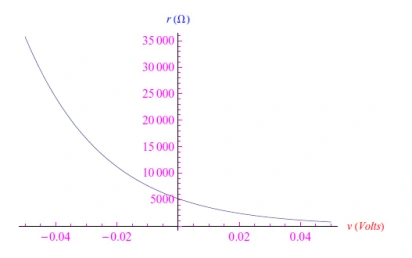
图9:作为v函数的微分电阻。注意反向极化的快速增加
在本教程中,我们会将[4]中描述的说法推广到所有半导体,根据该说法,对于锗(Ge)和硅(Si),温度每升高10°C,反向饱和电流就会增加一倍。
我们先回忆一下二极管的电压-电流特性:

假设i0与温度无关是一个近似值,因为i0取决于给定温度T下处于热力学平衡的载流子(电子和空穴)的浓度。这意味着i0取决于T。
[4]中描述的经验法则如下:
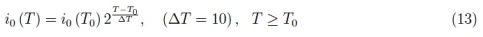
等式(13)对Ge和Si半导体有效。更广泛地,我们可以这样写:
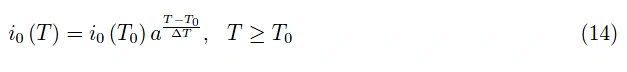
其中a是≥2的实数。经过简单的步骤,我们得到以下内容:
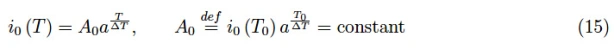
因此我们可以得出结论,对于任何半导体,反向饱和电流随温度呈指数增加。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: differential resistance and reverse saturation current,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯