
在半导体中,导电的物理机制与金属的物理机制完全不同。因此,我们预计会出现新类型的噪声。本文探讨了半导体器件中的各种噪声源。
在之前的教程中,我们使用电压-电流特性研究了二极管的行为与温度的关系:
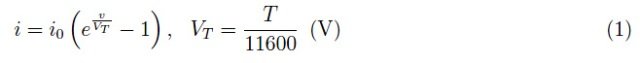
由于工作温度并非精确恒定的,而是在一个平均值附近波动,因此我们预计电流会随机波动。这可以用Mathematica仿真,因为这种环境非常适合高斯随机变量的实现。在图1中,我们报告了工作温度的趋势,平均值为T0=300K。
如果我们向二极管施加一个正弦信号,则电流的测量会返回图2的趋势,在这里我们看到了噪声的存在。
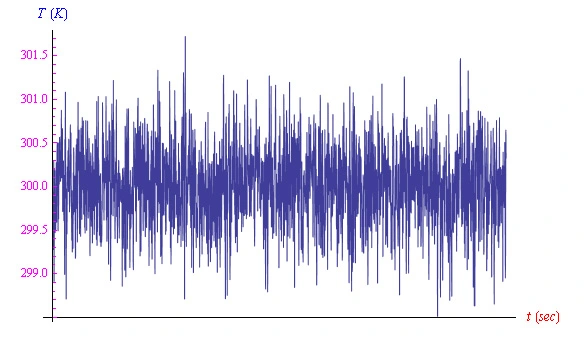
图1:工作温度随机波动
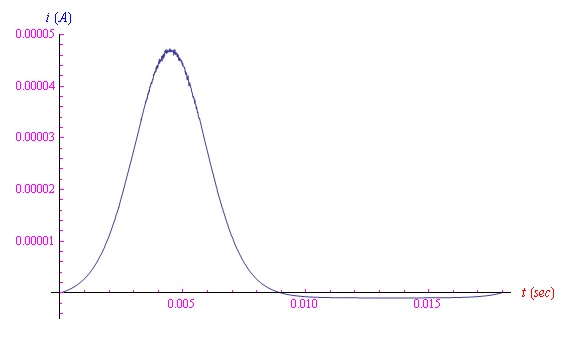
图2:存在热波动时二极管中的电流趋势
散粒噪声是电荷量化的结果。理想情况下,后者可以通过连续分布(即流体)来建模,前提是它具有极高浓度的载流子,例如发生在金属中。另一方面,在半导体中,浓度较低,因此不能忽略粒子方面。类似于雨落在屋顶上。在强度较低的情况下,单位时间内撞击屋顶的水滴数量相对较低,并且波动较大。这会导致压力在平均值附近波动。
在半导体中,共价键的断裂是由热能决定的。对于每个断开的键,都会产生一个电子-空穴对,并且电子会跃迁到导带。这就是电荷载流子的产生过程。相反的过程是重组,自由电子被不饱和共价键捕获。
重组是一个随机过程,散粒噪声是其结果。事实上,这会导致载流子浓度随机波动,从而导致电流强度随机波动。这种波动可以通过我们用τ表示的电荷载流子的寿命来描述(为简单起见,我们考虑电子和空穴的单一寿命)。准确地说,单个波动随时间常数τ呈指数消失,并且很容易使我们相信随着τ的减小,波动在时间上是不相关的,从而仿真白噪声(在100%不相关的极限情况下)。这可以通过确定各自的自相关函数来严格验证:应用著名的维纳-辛钦定理可以得到一个波动的功率谱,如图3所示,该谱在截止频率为τ-1的情况下是平坦的。由于重组中心的可能增加,该光谱变得非常平坦,这可以通过通常由杂质制成的所谓陷阱来实现。
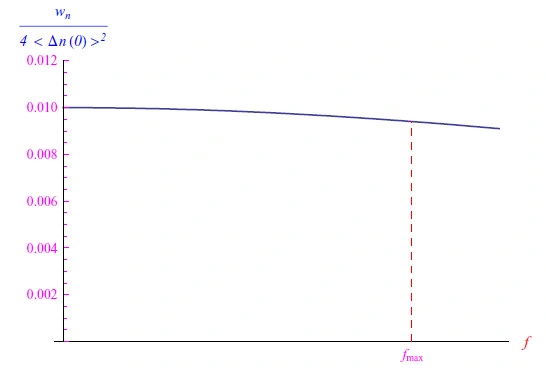
图3:电子浓度波动的散粒噪声功率谱
我们通过观察得出重组过程具有一个有趣的能量解释。为简单起见,我们考虑未掺杂的半导体(否则修改是显而易见的)。虽然成对(电子、空穴)的产生需要一定量的能量(例如热能),但重组会以热量的形式释放一小部分能量输入,这反过来有利于进一步共价键的断裂。
正如在之前的教程中所研究的那样,耗尽层的特征是两个电荷载流子的双势能势垒。即使所涉及的电荷没有足够的能量来穿越这个势垒,量子穿越的概率也非零(隧道效应)。该概率又由介于0和1之间的传输系数T量化,并与屏障的几何尺寸(高度、宽度)成比例。物理上,T取决于结的掺杂。根据这些参数,Esaki创造了一种利用量子力学所预见的隧穿过程的设备。
从电路的角度来看,我们期望在反向偏置下具有高电导率。更准确地说,隧道二极管的电压-电流特性如图4所示。
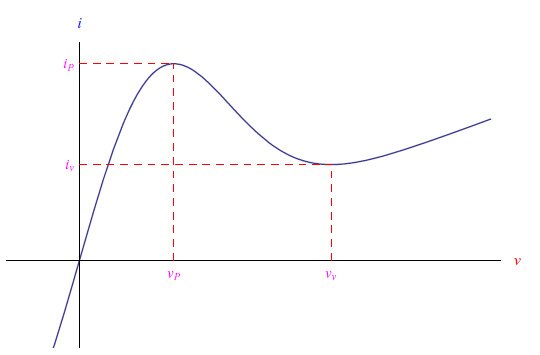
图4:隧道二极管的电压-电流特性
在正向偏置和0<v<vP(约50mV)范围内,电流迅速增加到峰值iP。这种趋势是由于隧道效应,由于与泡利不相容原理相关的机制,隧道效应往往会抑制更高的电压。对于v>vP,电流迅速下降,直到电压为vv(约60mV)。对于v>vv,pn结的典型传导占主导地位;这样,隧道二极管特性的最终趋势是合理的。因此,我们看到,在vP<v<vv范围内,隧道二极管具有负电阻。
在图5中,我们报告了隧道二极管的符号,而在图6中,绘制了等效电路。
各种尺寸的典型值是:
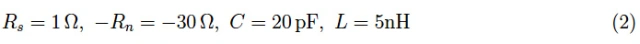
图5:隧道二极管符号
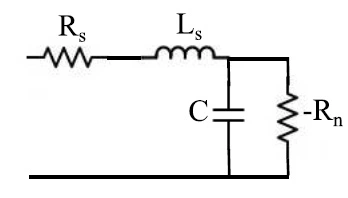
图6:隧道二极管等效电路
我们通过观察得出隧道二极管用于制作超快速开关的结论,因为隧穿过程在电路时间尺度上几乎是瞬时的。它还具有低噪声电流。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Noise in Semiconductor Devices,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯