
在介绍了变容二极管和pn结的扩散电容之后,我们将证明这种器件可以通过串联RLC来描述,其中电容器的可变电容是板上存在的电荷的函数,在结处具有不连续性。这就决定了确定性混沌的存在。
在图1显示了一个反向偏置的pn结:负极连接到p侧。这导致电荷载流子远离耗尽层的边缘。后者随之扩大,因此过渡电容CT也随之下降。从势垒的角度来看,也可以得出同样的结果,因为反向极化增加了势垒的高度,在开路时势垒等于eV0,其中e是电子电荷的绝对值,而V0是接触电势(或内建势),而在反向偏压下它是e(V0+|V|),根据惯例,反向偏压时V<0,反之亦然。
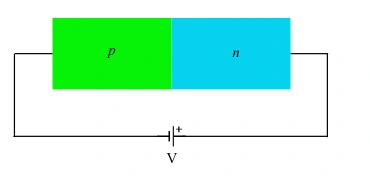
图1:反向偏置pn结
自由电荷向p和n两端扩散的过程是一个瞬变过程,很快就消失了。事实上,空穴向p侧(图1)左边缘的稳态扩散需要从n侧“供应”尽可能多的空穴,而在n面他们只占少数。在瞬态结束时建立的是由于少数载流子引起的电流,即反向饱和电流,在之前的教程中已经研究过了。这就证明了随着温度的升高,反向电流的增加趋势。
另一方面,在正向偏置中,过渡电容由于势垒高度的降低而增加,现在为e(V0−V)。然而,正如我们将要看到的,正向偏置由另一个电容决定。
过渡电容是一种寄生电容,尤其是当二极管用于阻止高频信号传输时。这可以通过研究图2所示等效电路的行为来理解。其中Rs是二极管本体的电阻,r是反向偏置的动态电阻,约为MΩ。另一方面,电阻Rs低得多。
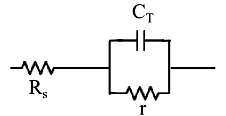
图2:描述过渡电容的等效电路
在某些应用中,会使用过渡电容,相应的器件称为变容二极管(varicap或varactor),其符号如图3所示。主要应用在无线电接收机天线选择器中。
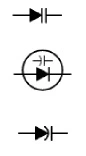
图3:变容二极管符号
pn结的正向偏置降低了势垒的高度,这导致耗尽层的减少。然而,在这种极化状态下,由倾向于在结附近积累的电荷扩散过程引发的电容效应占主导地位。因此,我们有:

称为扩散电容。另一方面,在正向偏置中:

所以

我们引入一个时间常数τ(它实际上取决于t,但作为一级近似值,我们可以认为它是常数),使得

在(3)中替换后返回:

其中r是动态电阻,在正向偏置中:
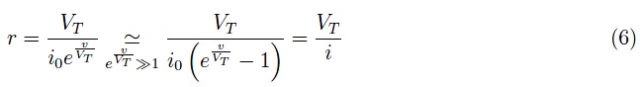
从而(5)被改写为:

我们得出结论,在正向偏压下,散射电容随电流线性增加。在反向偏置中:

证实前面的论点。从(5)中我们看到τ是电容支路r的时间常数,CD,它在任何情况下在电路时间尺度上都很小。实际上在直接极化中是r<1; 在反向偏置中CD≪1。
等式(4)让电流强度与电荷Q线性相关,并提供了一个pn二极管的电荷控制模型。这种表示方法相对于电压-电流特性的优势是在于(4)的线性。线性得以保留,但有时,如果我们转到电压-电荷表示:

其中Vγ是失调电压。
在Wolfram Library Archive 网站目录中有一个Mathematica笔记本,它仿真蔡氏二极管的行为。
我们使用所谓的机电类比重新研究了这些概念:控制串联LC电路行为的方程在形式上与质量为m的粒子与弹性常数为k的理想弹簧相关的方程在形式上相同,前提是自感系数L替换为m(代表惯性),电容C替换为弹性常数的倒数。在实际描述中,LC电路具有一个电阻分量R,对于它来说串联RLC被考虑。欧姆电阻的机械对应物由摩擦力或更好的黏度系数b表示。
施加到串联RLC的电压v(t)在相应的机械系统中表示为一个随时间变化且遵循相同定律的力。
所以在电荷控制模型中,一个pn结相当于一个可变电容的电容器,它是电荷Q的函数:
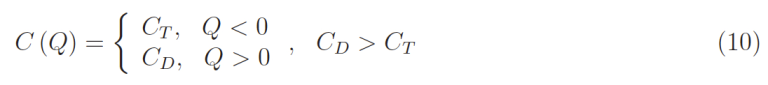
作为一级近似值,我们可以考虑CT、CD这些量是常数。在任何情况下,电容C在结处都有一个有限的不连续性。在机电等效中,非零的自感系数L是不可避免的。事实上,如果L=0,上述等效将失去自洽性,因为会有一个无质量粒子受到弹力场的影响,这是无稽之谈(在经典力学的范式中)。因此,我们必须引入适当的自感系数,然后考虑欧姆电阻的存在。我们得出结论,pn结等效于串联RLC,电容C根据(10)变化。在我们的分析中,我们建立了分段线性振荡器运动的微分方程,该振荡器被阻尼并受到周期性力F(t)= Fmax sin Ωt − Fγ,其中Fγ是失调电压的对应量。执行由机电类比引起的替换,我们得到一个微分方程。通过结合适当的初始条件并使用与Wolfram Library Archive中存在的相同数量级的数据,我们得出了与图4的相位图(该图显示了奇异吸引子的存在)和分叉图(图5)中说明的相同结论,这是确定性混沌的典型元素。

图4:相位图
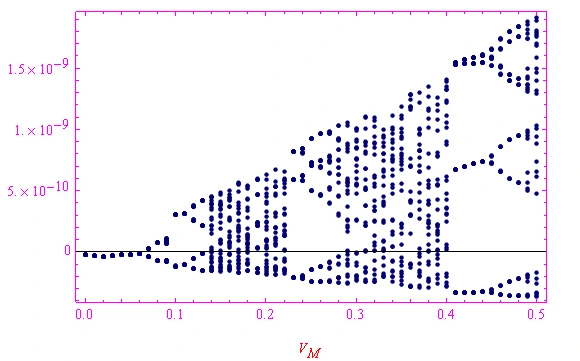
图5:分叉图,纵坐标为电荷Q
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: The Varicap Diode,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯