
这本关于电力电子的笔记的结构如下:
阅读这些教程的需要电气工程的基础知识。
考虑图1中所示的电路,该电路由一个带有电容滤波器的理想二极管组成,我们想确定什么条件能使纹波最小化,即输出电压的残余振荡。
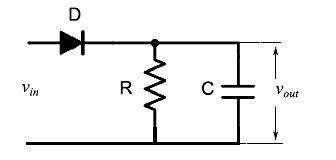
图1:带电容滤波器的整流器
我们假设将以下正弦输入电压施加到电路:vin(t)=VMsin(ωt),其中ω=2πf是脉动,f是频率。由于其理想性,二极管在正半波(正向电压)期间表现为短路,在负半波(反向电压)期间表现为开路。如果在时间t=0我们关闭电路,在瞬间t1=π/(2ω)输入电压vin达到其峰值,由VM给出。由于我们忽略了二极管的内阻,对于所有正半波,我们有vout=vin。然而,如果电容器C通过负载电阻R的放电过程在正弦振荡v{in}的时间尺度内是瞬时的,也就是说如果时间常数τc=RC远大于振荡周期,则会发生这种情况。然而,通过这种方式,残余振荡(纹波)达到其最大值,等于输入信号。
为了获得合适的整流器,我们需要尽量减少这种振荡。这个结果可以通过插入一个容量足够大以满足以下条件的电容(通常是电解电容)来实现:

因此,输出信号呈指数下降趋势:
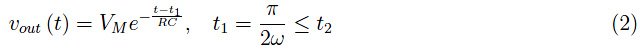
下一个正半波(t=2π/ω)将使二极管回到导通状态,允许电容器重新充电,直到达到峰值VM。随后,放电过程将再次发生,并且循环将以与输入信号相同的周期重复。输出电压具有振荡趋势,如图2所示,其振幅低于输入电压。平均输出值为Vout,而峰间幅值(纹波)由下式给出:

若RC≫t2−t1,将泰勒级数的指数式(3)展开,可写出如下方程:
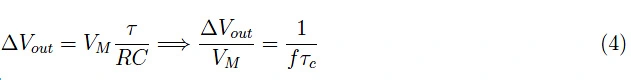
要使条件∆Vout≪VM为真,它必须是τc≫f,正如我们假设的那样。
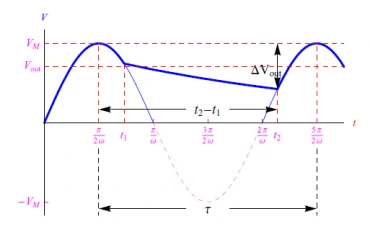
图2:输出电压图
假如我们被要求重建前面教程的输出信号,假设工作温度为T=500K。。
对于本教程,我们将参考图3中所示的更真实的电路,其中我们仍然有一个正弦输入电压。
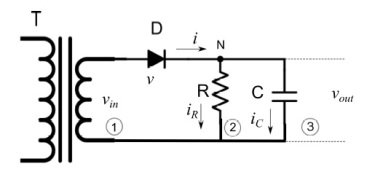
图3:更真实的电路
在使用任何软件工具(如Mathematica、Maxima、Matlab或类似工具)之前,关注问题的物理特性非常重要。例如,正如我们在之前的教程中看到的那样,残余电压振荡(纹波)的幅度取决于电容滤波器的时间常数τc=RC。这意味着必须满足条件τc≫ω−1,其中ω是正弦输入电压的角频率。因此,纹波的减少也取决于频率:不同频率的信号将被不同地过滤。图4和图5显示了两个频率不同但电路参数相同的正弦波输入产生的输出电压的变化趋势。
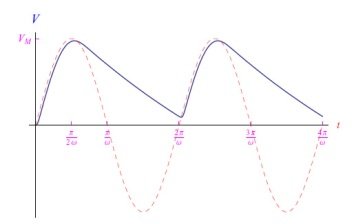
图4:输出电压图,其中ω=2π rad/s,τc=2s。虚线是输入电压
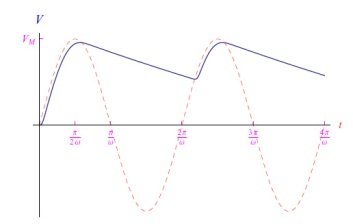
图5:输出电压图,ω=2π rad/s,τc=2s。虚线是输入电压
我们处在一个非线性动态系统,它接受正弦电压vin作为输入并返回电压vout(t)=x(t)>0作为输出,没有负半波和残余振荡电压(纹波)。通过应用基尔霍夫原理并使用众所周知的二极管电压-电流特性,我们可以写出具有初始条件的微分方程。由于二极管的非线性,方程是一阶非线性的。该系统是不可逆转的,这意味着输出信号是由输入信号唯一决定的。
使用Mathematica开发的相应算法表现出计算的不稳定性,这是由于作为系数进入微分方程的脉冲项,决定了计算过程中的溢出。不稳定性发生在温度T≤500K时。我们将研究方程在T→0的极限下的行为。这个过程是形式上的,因为在绝对零度下,半导体表现得像绝缘体。此外,二极管通常的电压-电流特性在低温或极高温度的限制下不再有效。我们设法证明了一个定理,根据该定理,尽管存在狄拉克δ函数类型的“无限”峰(在极限T→0),输出电压是一个没有奇点的函数。
然后,我们对T→+∞进行了极限分析,得出了一个不一致的结论,即动态系统失去了确定性,因为对于任何输入,输出信号都为零。图6、图7和图8报告了我们的计算分析摘要。
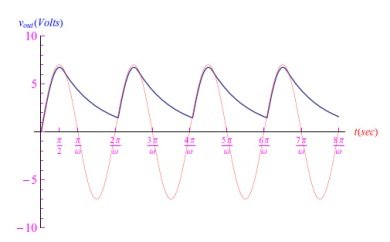
图6:R=104Ω时的输出电压
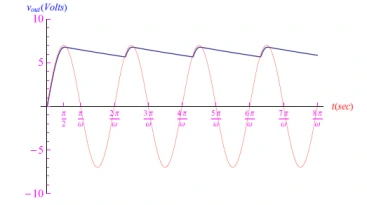
图7:R=105Ω时的输出电压
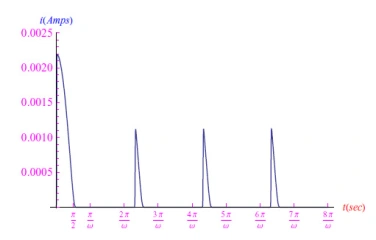
图8:二极管中的电流
在本教程中,我们将在以下条件下使用二极管和电容滤波器仿真包络检测器:
我们将参考图9中所示的包络检测器电路。如果vm(t)是转换为电信号的声学信号(即低频或LF信号),则调幅包括调制一个正弦射频载波信号的幅度。使用正弦低频信号作为输入,得到的调幅信号如图10所示。
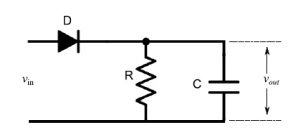
图9:包络检测器
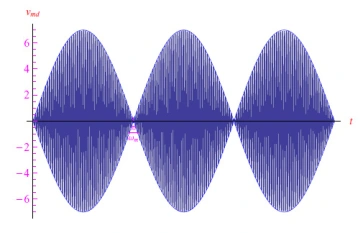
图10:调幅信号的趋势
为了提取原始低频信号,必须对调幅信号进行解调。对于图9的电路,vin=vmd。对于合适的R、C值,电容器通过电阻放电,跟随调制包络或低频信号。从分析上讲,我们需要对上一个教程的微分方程进行积分。对于R=102Ω、C=10−7F、i0=1µA,并使用Mathematica进行数值积分,我们获得了图11中所示的输出信号图。
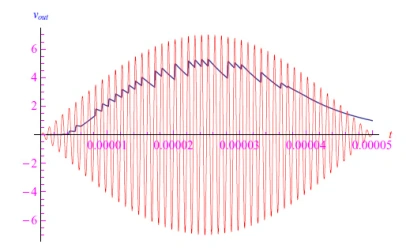
图11:发出信号的曲线图,注意电容器的放电情况
到目前为止,我们假设完全没有噪音。现在,假设我们有一个如图12所示的噪声输入信号。通过将微分方程与噪声项积分,我们获得图13所示的输出趋势。
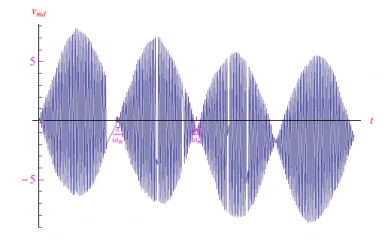
图12:浸入布朗噪声中的调幅信号
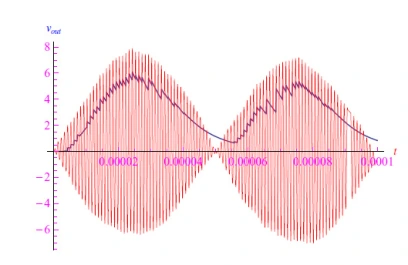
图13:存在布朗噪声时的解调
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Ripple and Envelope Detector,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯