
这本关于电力电子的笔记的结构如下:
阅读这些教程的需要电气工程的基础知识。
在这篇关于电力电子的文章中,我们将研究工作温度远高于环境温度的碳化硅(SiC)整流器的行为。我们可以将电路想象成必须在“热环境”中工作的机电牵引系统。
在图1中,D是宽禁带(WBG)半导体二极管。对于正弦输入,我们谈论的是温度远高于300K(即室温)时的输出电压。我们还假设负载电阻是已知的。
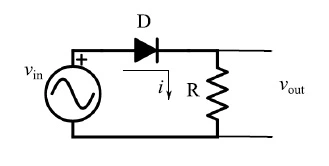
图1:半波整流器
从[4]可以看出,电流i由下式给出:

我们可以快速回忆一下等式(1)中涉及的各项。量v是二极管两端的电压降;i0项是反向饱和电流,约为1µA;参数η是无量纲的,我们可以将其近似为1。VT是一个电势,由下式给出:
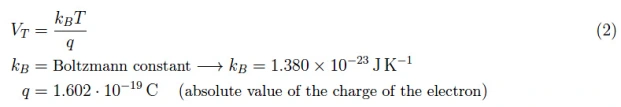
从(2)中,我们可以看出VT包括二极管和整流器在变热时的行为方式。(1)中使用基尔霍夫第二原理来确定二极管两端的电压:

通过进行适当的替换,我们获得频率为f的正弦输入:
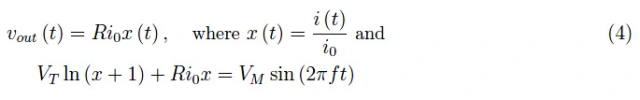
现在必须在软件中找到(4)在高温限制中的解决方案。对于R=10kΩ、VM=120V和f=50Hz,通过使用Mathematica求解,我们获得了T=600K的曲线图,如图2和图3所示。
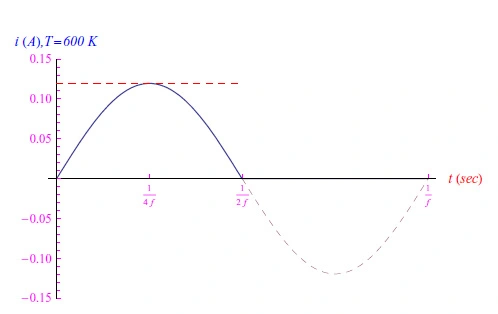
图2:电流图
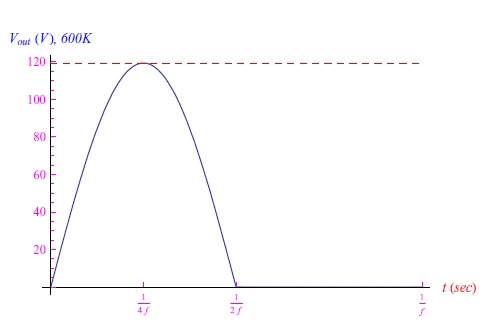
图3:输出电压图
现在,我们来看看这个幅度的电路含义:

被称为温度的电压等效值。从(1)中,假设η=1,我们看到:
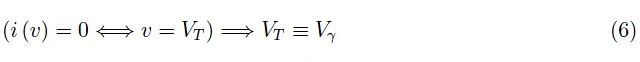
其中Vγ是二极管的失调电压。因此,我们可以说明如下:
温度的等效电压是失调电压。
因此,将二极管置于高于300K(典型室温)的温度下相当于增加失调电压。更准确地说,我们获得了图4中所示的曲线图,其中我们还看到,对于相同的v,电流随着T的增加而减小。发生这种情况是因为,随着温度升高,二极管的微分电阻(大约等于VT与电流i之间的比率)增加。SiC半导体可以比硅或锗更好地散热,因为它们具有高导热性。这意味着他们不需要散热器。但是,我们将不得不在下一个电力电子教程中研究温度对工作点的影响。
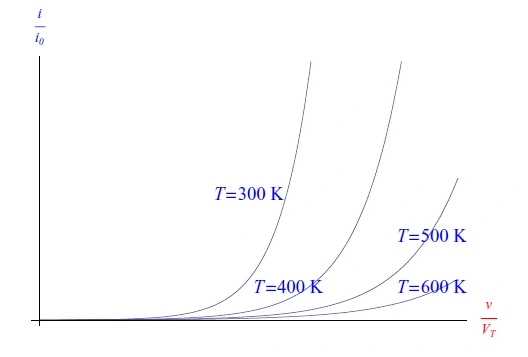
图4:电流图(在i0上归一化)作为电压v的函数(在VT上归一化)
从热力学的角度来看,量VT是热能kBT与电子电荷的比值。最后,我们看到(1)对于给定的温度区间是正确的,但在T→0的极限情况下不是,因为任何半导体在绝对零时都是绝缘体。
Bob是一名电气工程师和电力电子爱好者,正在努力进行一组与WBG二极管(图5)相关的测量,如图6所示。他想使用电压-电流特性计算工作温度,假设反向10µA的饱和电流。
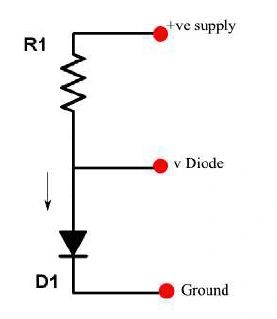
图5:用于测量的电路
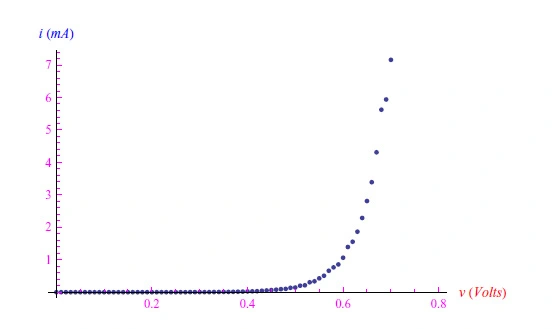
图6:Bob执行的测量图
使用Mathematica,第一步是对测量数据列表中的各种项进行排序。然后Bob将不得不执行半对数刻度拟合。准确地说,我们将电压-电流特性近似如下:
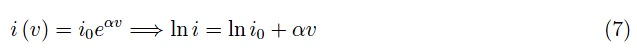
其中α=V−1是要确定的参数。通过将电压-电流特性近似为指数,可以得到具有线性趋势的半对数刻度图,如图7所示。
使用拟合操作,我们得到:
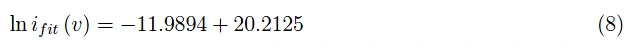
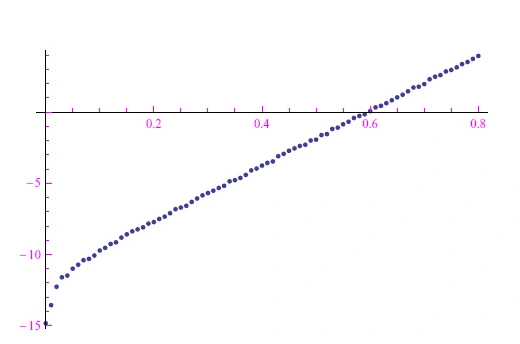
图7:Bob在半对数刻度中执行的测量图。该图是通过Mathematica计算环境中列表的Listable属性获得的。
切换到线性刻度并与实验室数据一起绘图,我们得到图8。它如下:
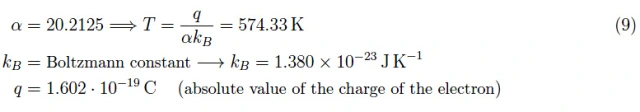
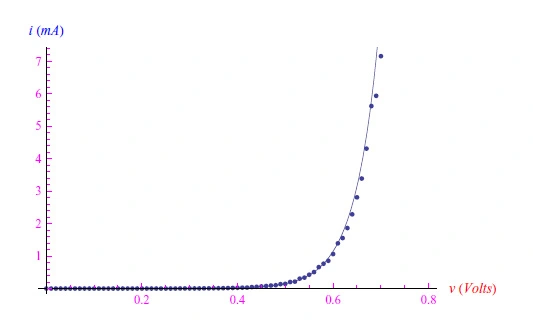
图8:数据与拟合比较图
参考本节的第一个教程,我们想确定当温度升高或降低时会发生什么。
据我们所见,该问题可以通过以下方程组求解:
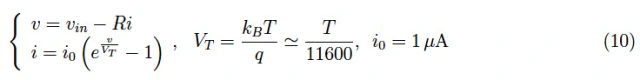
可以用Mathematica解决。但如果您想查看工作点如何移动,最好在笛卡尔平面(v,i)中以图形方式进行。这些方程中的第一个(10)表示负载线。而第二个是电压-电流特性。出于可视化目的,我们可以更改负载电阻值,设置R=2Ω。假设二极管现在处于正向电压,vin=0.33V,我们得到(在T=300K时)v=0.268V和i=0.032A(图9)。
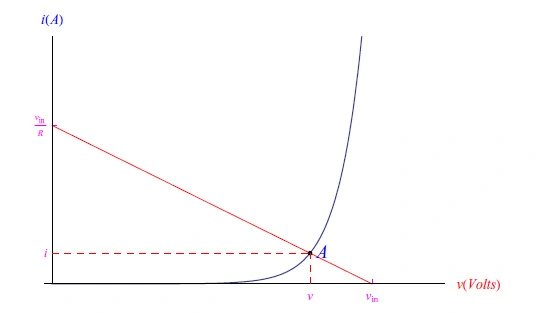
图9:系统的图形化解决方案(10)
负载线法仅适用于静态条件。由于角系数与保持不变的负载电阻相反,因此当vin变化时,负载线会平行于自身移动。温度变化引起的工作点偏移(如图10所示)更为有趣,因为它可能会影响半导体器件的工作方式。
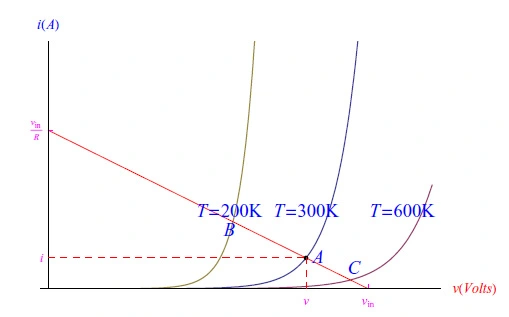
图10:温度偏移后工作点沿负载线的移动
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Rectifier and WBG,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯