
这本关于电力电子的笔记的结构如下:
阅读这些教程的需要电气工程的基础知识。
假设我们要解决一个问题分为以下两点:
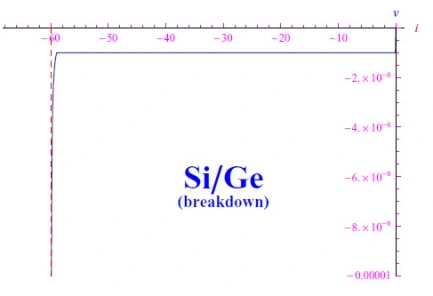
图1:Si/Ge二极管的击穿电压图
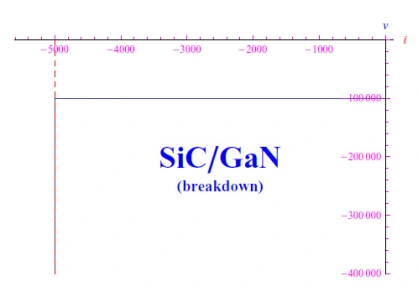
图2:SiC/GaN二极管的击穿电压图

图3:确定硅二极管的δV
我们可以再次回顾电压-电流特性,由以下等式给出:

对于v>0,二极管处于正向电压模式,而对于v<0,它处于反向电压或阻断模式。在反向电压模式下,我们有:
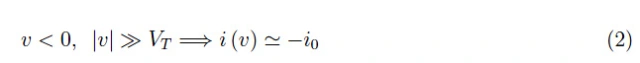
在这种情况下,二极管的动态电导几乎为零(动态电阻无穷大)。通过逐渐增加反向偏置电压,电荷载流子生成过程“爆炸”成奇异点(至少在理论上是这样):

其中阈值vB<0为击穿电压,即反向饱和电流急剧增加时的电压。这种奇异行为可以通过两种机制来解释:
雪崩倍增是由于电场强度增加导致共价键断裂。晶格离子碰撞释放的相应电子/空穴对产生新的电子/空穴对,如此反复。
另一方面,齐纳效应不涉及晶格离子。在电路应用中,这两种效应没有区别。因此,我们简单地参考齐纳效应并通过设置Vz=−vB来定义齐纳电压。
我们还记得,虽然禁带的振幅εg随着温度的升高而降低,但反向饱和电流会增加。那么很容易理解齐纳电压与禁带成正比。更准确地说,它的范围从Si/Ge二极管的不到1V到SiC/GaN二极管的5000V。i0也显着增加:对于Si/Ge,典型值在1–10µA范围内。
众所周知,齐纳二极管用作稳压器。在不涉及高功率过程的电路中,需要大约10V的稳定电压。我们使用v>vB+δV的电压-电流特性绘制了图3的曲线,其中0<δV<−vB,然后将其与 "测试函数 "的图形联系起来,对于该函数,不可能在结点处施加一导数的连续性。事实上,我们注意到典型的“尖锐拐点”对应于二极管动态电阻的不连续性。原则上,小增量δV是固定的,以免电流值下降到低于二极管制造商提供的阈值(否则没有稳定性)。
图4中所示的原理图包括具有以下特性的设备:VL=5V和IL=50mA。我们还有一个电源,提供电压Vin=15V。使用工作点Vz=5.1V和Iz=50mA且最大功耗为0.5W的齐纳二极管,确定电流的范围在负载可以变化。
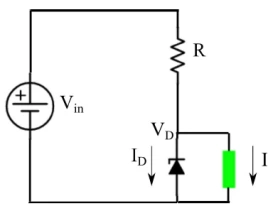
图4:稳压器原理图
对于理想的齐纳二极管,其电压-电流特性具有图5所示的趋势。但是,最好改用绝对值,如图6所示,用大写字母表示相应的量。
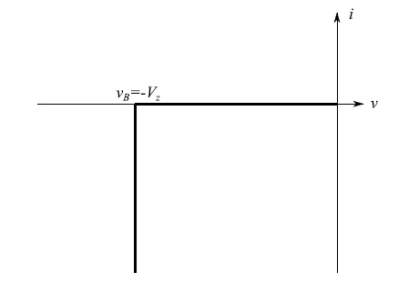
图5:理想齐纳二极管的电压-电流特性
理论上,如果VD=Vz(该值由二极管制造商提供),电流可以在0到+∞之间变化。实际上,电流的最大值会产生二极管能够耗散的最大功率Wmax(该数值数据也由制造商提供)。
因此,我们有:

此行为如图6所示,其中A(Vz,Iz)是工作点(Iz=已知数值数据)。
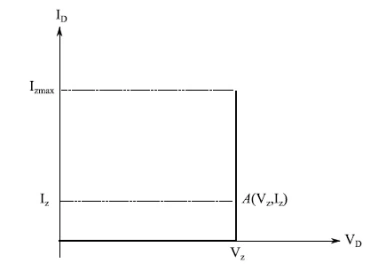
图6:理想齐纳二极管的电压-电流特性
应用基尔霍夫第二定律,我们有:

在右侧,我们有负载中的电流I,其大小可以围绕标称值IL波动。如果I=IL,二极管配置为ID=Iz。设VD=Vz,等式(5)变为:

这使我们能够计算要插入电路中的电阻R的值:

因此我们可以写:

从中我们可以将负载中的电流表示为二极管中电流的函数:
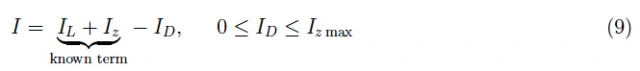
相应的图如图7所示。我们现在可以得到稳定范围如下:
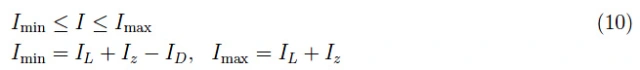
换句话说,如果负载中的电流在等式(10)给出的范围内变化,电压将保持稳定在VL。现在,我们所要做的就是将数值插入到我们的方程式中。我们获得:
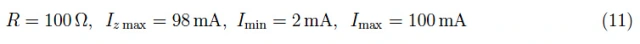
总之,即使负载中的电流在50mA的标称值附近波动,在2mA至100mA的范围内,器件两端的电压仍保持稳定在VL=5V。
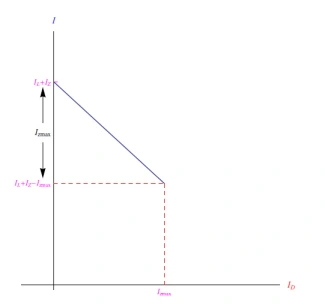
图7:稳定范围
在图8所示的原理图中,D1和D2分别是锗和碳化硅二极管。该系列由提供电压V0=50V的电池供电。Vz是二极管D2的齐纳电压,假设工作温度T=400K,并且D2的反向饱和电流是二极管D1的40倍。
假设我们要解决一个问题分为以下两点:
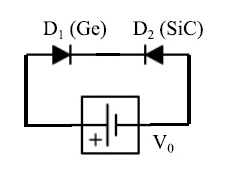
图8:Ge和SiC二极管系列
就电压而言,我们将使用小写字母表示变量(v、v1、v2、...),使用大写字母表示常数。
鉴于此,我们将找到一个使用电压-电流特性的解决方案。二极管D2处于反向电压模式,其行为如图9所示。该二极管迫使发电机提供等于D2反向饱和电流的电流强度,我们用i02表示。穿过二极管D1时,该电流会导致电压下降V1,这可以使用图10中所示的D1的电压-电流特性来确定,并由下式给出:

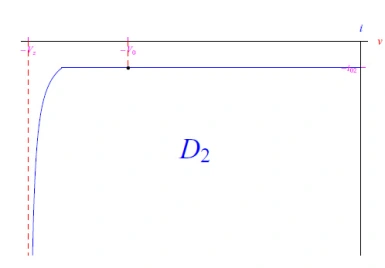
图9:二极管D2的反向电压图
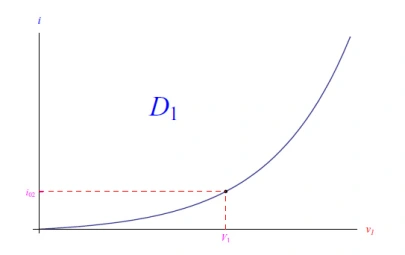
图10:二极管D1的正向电压图
从等式(12)我们可以写出:
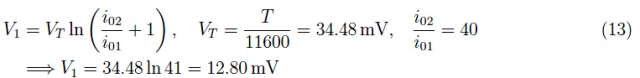
根据基尔霍夫第二定律,我们有:

如图11所示,在这种情况下我们有:V0>Vz。
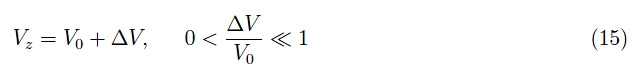
考虑到基尔霍夫第二定律,D1两端的电压降为V1=∆V。电路中流动的电流强度可以根据D1的电压-电流特性计算如下:
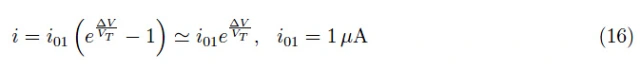
二极管D1消耗的功率由下式给出:
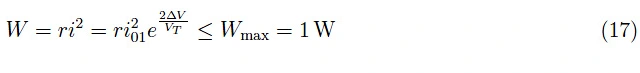
然后我们可以得到解决方案:
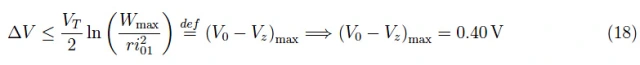
总之,电源电压可以低于Vz直到0.40V。
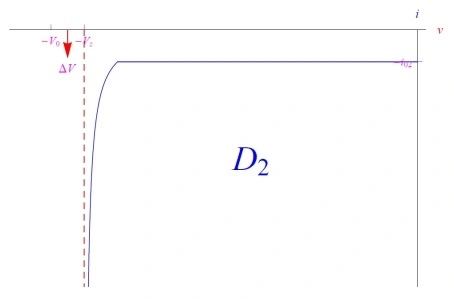
图11:二极管D2的电压-电流特性
 最前沿的电子设计资讯
最前沿的电子设计资讯