
这本关于电力电子的笔记的结构如下:
阅读这些教程的需要电气工程的基础知识。
入射到半导体晶体上的电磁辐射的能量有利于导电性,前提是构成辐射的光子的能量大于禁带εg。回想一下光子能量与频率的关系,然后用波长表示,可以得到电离条件如下:
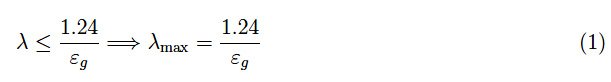
其中能量单位为eV,波长单位为µm。对于硅和锗,我们有:
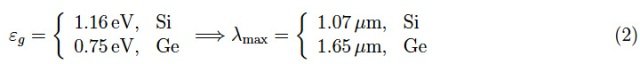
我们可以使用禁带较小的半导体来达到约6.9µm的波长。然而,我们是在可见光和远红外波段。图1显示了光电导体的基本示意图:电场E是由电池产生的,它在半导体上建立了电势差。
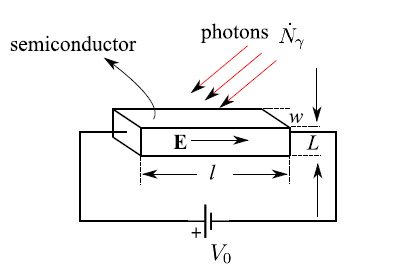
图1:光子通量撞击半导体
如果满足条件(1),则电子-空穴对通过热和光子方式产生。因此,电流可以表示为这两个贡献之和:

其中iγ是光电流(由于光子产生的电荷),it是热产生的分量。对于天文探测器中使用的光电导体来说,有必要将热贡献忽略掉,因为它是一个噪声源。这可以通过用低温技术冷却系统来实现。图1中所示的光子,即每单位时间和单位表面积(晶体的上表面)的光子数由下式给出:

假设均匀照射,通量可以被认为是恒定的。将概率η称为光子电离共价键量子效率,单位时间内产生的电荷数由下式给出:

其中S是晶体上表面的平面,a是一个常数因子,我们可以将其设置为等于2,因为每个光子以概率η释放两个电荷。回顾一下迁移率µ的定义,可以确定偏置电路中电子的流动(空穴的流动可以忽略不计,因为它们的迁移率较低)。通过与光子流的关系,我们得到光电导增益:

其中τ是电子的平均寿命。通过这种方式,光电导体的行为就像一个将光转换为电流的转换器,其效率为ηGpc。天体物理学中使用的典型值如下:
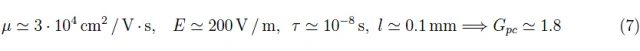
光电导体的光谱响应(或响应率)由下式给出:

其中Wγ是输入辐射功率。在分子中,我们必须考虑对电流的贡献(光子、温度)。在天体物理学中我们可以写:
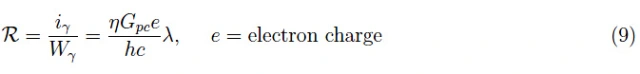
在理想条件下,η不依赖于波长λ,因此响应率随λ线性增加,直至达到方程(1)给出的截止λmax。图2对此进行了说明。由于电流的热分量在接近截止的波长中占主导地位,响应率不断降低,因此我们预计会出现图3所示类型的趋势。
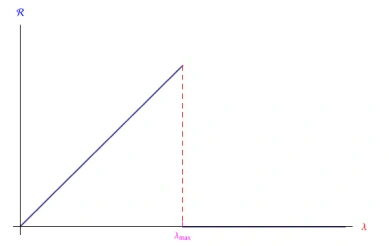
图2:光电导体的响应率,其中对电流的热贡献可以忽略不计
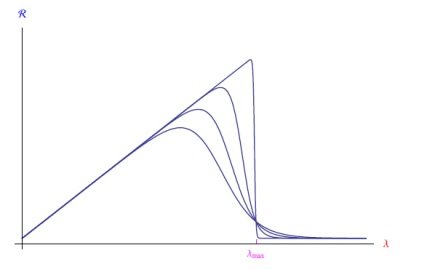
图3:光电导体响应率的可能趋势,其中对电流的热贡献不可忽略
我们研究了本征半导体的光电导率。下一步是由光子通量照射的pn结。我们可以注意到以下实验数据:一个反向偏压和发光的pn结被一个电流穿过,这个电流随着光子通量的增加而线性增加。
让我们考虑n型半导体,并假设n0,p0为平衡时电子和空穴的浓度。如果在某一时刻我们“照亮”晶体,上述浓度将经历相同的增加Δn=Δp>0。然而,由于半导体是n型,增加的百分比是非常不同的。确切地说:
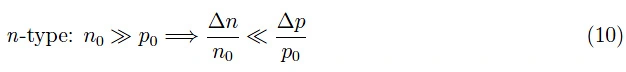
当切换到p型半导体时,同样的论点也适用,其中上述角色显然已互换。
总之:光子通量几乎只作用于少数载流子。这可以表示为,辐射的行为就像少数载流子的注射器。
在pn结中,由于反向饱和电流是由n区和p区各自的少数载流子引起的,因此辐射有利于该电流的增加。让我们回顾一下电压-电流特性:

其中:i0>0是反向饱和电流,VT是温度的伏特当量,而v是施加的“la d.d.p.”,正向偏压时v>0,反之亦然。通过改变电流的符号,使i可以被绘制为v的函数|v|,当v<0时,我们有:

照射二极管会增加电流,因此我们需要添加iγ项:

当iγ=0时,我们得到“暗电流”,即典型的反向饱和电流,其图形穿过原点。反之,当v=0时,只有iγ在电路中循环,因此等式(13)的图形不经过原点。从相同的方程中,我们看到总电流随着施加相同的反向偏压而增加,增加了发光强度(因此是iγ)。简而言之,我们获得了如图4所示的一系列特性曲线。图5显示了光电二极管符号。
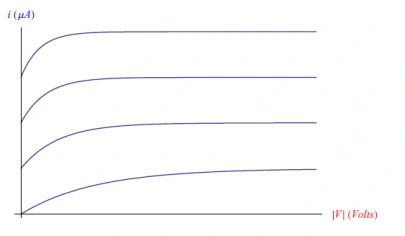
图4:光电二极管的电压-电流特性曲线
图5:光电二极管符号
关于正向偏压,最好讨论势垒。我们在上一期中看到,pn结具有内置电势V0,它对应于高度为eV0的势垒,e是电子电荷的绝对值。通过在开路中照射晶体,电磁能有利于将势垒降低一定量,该量除以e,返回电势Vγ(称为光伏电势)。这可以通过将等式(13)的第二边设置为零来分析看出。我们获得:

从方程(14)我们可以看出,Vγ随iγ呈对数增加,因此也随光通量呈对数增加。
LED使用与光电二极管特性相反的物理过程。事实上,后者吸收光能以返回电力,而LED则吸收电力以发光。原理上,是电子-空穴重组的过程提供能量。准确地说,我们必须提供能量(热能、光能)来电离共价键。在量子力学框架中,如果ΔE是空穴和电子各自占据的能级之差,则在重组过程中将发射出一个频率的光子:
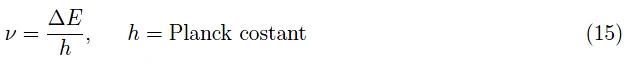
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Photodiodes and LEDs,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯