
在“碳化硅和氮化镓的晶体结构”(Crystal Structure of Silicon Carbide and Gallium Nitride)一文中,我们简要讨论了固体的晶体结构。在该特定情况下,我们指的是半导体,但这些概念也很容易延伸至金属。众所周知,经过充分测试的电化学过程让金属得以通过氘(氢的一种重同位素)而“充电”(带电荷)。因此,研究这些晶格结构在低温极限下的行为并导入超导现象(superconductivity)的概念是非常有趣的。
金属的电阻率是温度的递减函数。对于大多数金属来说,T→0时达到极限值,其中T是待研究样本的绝对温度。然而,在高于绝对零度以上的临界温度Tc时,有些金属的电阻率就会消失。
1911 年,Kamerlingh Onnes 发现水银(汞)的临界温度Tc等于4.15K。在同一历史时期还发现了,锡的临界温度Tc等于3.72K,铝的临界温度Tc等于1.2K。然而,真正的转折点出现在1986年,人们发现镧、钡和铜的复合氧化物的临界温度为35K。
BCS是Bardeen、Cooper和Schrieffer三位物理学家的缩写。他们阐述了超导现象模型,本文将对此进行简要解释。
在金属中,电子构成一种特殊的“量子气体”,称为费米(Fermi)气体。电子是费米子,或半整数(具体为1/2)自旋粒子。在统计量子力学,理想的费米气体在低温下的行为是众所周知的。在此,所谓的理想是指气体粒子之间不存在相互作用。由于库仑(Coilomb)斥力,金属的传导电子的情况并非如此。然而,在零阶近似中,忽略这种相互作用是合理的,同时,统计量子力学返回了金属在导电性方面的行为——修正了旧的德鲁德(Drude)模型。
在进一步的近似中,由于添加屏蔽电势而考虑了电子之间的相互作用,即单个电子“看到”的不是邻近电子的裸电荷,而是被其余电子和晶格离子屏蔽的电荷。这就产生了费米液体的概念,由于弱相互作用,费米液体不同于费米气体。我们还必须考虑电子自旋的影响。电子倾向于以自旋单态(即零自旋)结合。尽管电子-电子库仑力具有排斥性,但这种情况还是会发生。
由此产生的电子对(Cooper对)在量子统计力学中被称为准粒子。粒子在物理上并不对应于这个实体。但是,它的行为可以用量子统计力学进行统计(和量子)描述。由此产生的物理系统是一种“理想量子气体”,因为单个粒子对之间的相互作用为零。它不是费米气体,而是玻色(Bose)气体,因为其成分的自旋为零(构成Cooper对的电子总自旋为零)。
“玻色气体”一词指的是它的组成成分遵循玻色-爱因斯坦(Bose-Einstein)统计的事实,众所周知,对于玻色-爱因斯坦统计量,泡利不相容原理(Pauli exclusion principle)是无效的,因而对于费米子(以及单个电子)也是无效的。由此可知,该系统表现出玻色-爱因斯坦凝聚现象:存在一个发生相变的临界温度Tc,在该温度下,宏观数量的Cooper对处于最低能量的基态。这种Cooper对产生了超电流,要解释其机理并不容易。打个比方,每对Cooper可以比作一对足球运动员,他们彼此不断传球,并设法躲避对方球员的擒抱,最终达到球门。在这个例子中,擒抱代表的是与晶格的碰撞,而球则是单电子的裸电荷。
让我们试着问自己:如果在金属中添加氘(重氢)会发生什么?我们知道,氘(D)是氢(H)的一种同位素:氢由一个质子p和一个电子e-组成,而氘核则由一个质子和一个中子n组成(图1)。
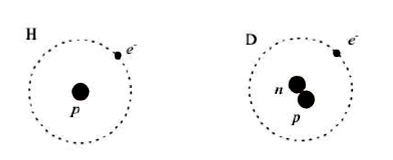
图1:H vs D。
因此,我们有一个电子气体和一个质子气体。根据初步的粗略近似,我们可以认为这两种系统与np(质子浓度)解耦,并与ne(电子浓度)的数量级相同。如果所使用的金属是超导体,那么只要降低温度,就可以在Tc时过渡到超导状态,这要归功于Cooper对的形成,我们可以用下面的符号来表示Cooper对:

质子的自旋也是 1/2,因此它们的统计量与电子相同。然后,它们会受到库仑斥力的作用,并像电子一样趋向于完成自旋态,形成自旋单子,由于这种自旋单子它们"接近"产生类似Cooper对的东西:

然而,相较于电子,质子可以通过释放能量来发生“聚变”。因此,不能排除在极低的临界温度下释放能量的过程,这可以通过增加质子的浓度来实现。据推测,由于需要达到很低的温度,使得精确观察和重现这一过程极具挑战性。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Superconductivity of a metal charged with protons,由Susan Hong编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯