
在这个框架中,晶体的原子核/离子被认为“静止”在各自的晶格位置上。由于电子比各自的原子核轻得多,因此电子的动态在原子核的时间尺度上可以被认为是瞬时的,通过观察可以直观地证明这一点是合理的。在这种情况下,我们可以将前者与后者分离开来。
对于半导体(室温下),单个电子的能量分布规律ε紧密遵循玻尔兹曼统计。相反,模拟原子核分布的势能的周期性决定了光谱能量的典型能带结构,其特征在于存在禁带,该禁带在任何情况下都低于绝缘体的禁带。而另一个鲜为人知的技巧是应用静态均匀磁场,正如已经证明的那样,半金属-半导体转变的发生要归功于相当强度的磁场。回忆一下,半金属的禁带为零,然而,传导电子的密度却远低于金属。
施加磁场H(或磁感应强度B)后,禁带的调制是由于电子的磁偶极矩µ与磁场H的相互作用而产生的。玻尔兹曼分布返回的是单个电子通用能级ε的占位数,而霍夫施塔特分布将磁场强度表示为ε的函数(变量已适当归一化)。这种分布是一种分形,称为霍夫施塔特蝴蝶(图1),其存在最近已在石墨烯中得到证实。

图1:霍夫施塔特蝴蝶
这一发现非常重要,因为霍夫施塔特提出的模型是抽象的,它指的是理想的二维晶体(顺便说一句,石墨烯是由单原子层碳原子组成的晶体),简单来说,2D晶体就是厚度是原子尺寸的晶体。因此,就各种(宏观)意义而言,石墨烯是一种2D晶体。霍夫施塔特模型图中的水平段代表了允许的能带。磁场的归一化是通过区间[0,1]内的无量纲参数α来实现的。为了阐明其含义,让我们来看看下面的情况:
这是两个问题,其确切的解决方案是已知的。在第一种情况下,电子是由所谓的布洛赫波(由具有相同周期性的函数在振幅上调制的平面波)描述的量子。而在第二种情况,由于粒子受到洛伦兹力的作用,因此可以通过求解牛顿第二定律给出的运动方程对电子进行经典描述,其符号表达为:

其中B0是静态均匀磁场,c是真空中的光速。运动是周期性的,周期TB与磁场成正比。布洛赫波也是周期性的,周期为TBloch。因此,上述参数α给出了两个特征周期以及求解的关键,定义如下:

在没有磁场的情况下,α=0,而α=1则表示TB=TBloch,即电子在磁场中的运动周期与布洛赫波相同。不过从数字上讲,这相当于施加数万亿高斯量级的磁场。而且,比值(2)可以是有理数,也可以是无理数。如果α是有理数,即两个整数p、q,例如α=p/q,则有q个允许的能带。否则,允许的能带数为零。实际上,后者被简化为拓扑学中所谓的康托尔集。
我们忽略了原子核/离子的运动。由于温度的原因,它们会围绕一个稳定的平衡位置做微小的振动,但讨论磁偶极矩的影响更有趣。正如上一部分提到的,半导体禁带的调制是由于电子磁偶极矩与B0的相互作用。根据经典电动力学,我们知道一个带电荷q和角动量L的粒的粒子具有磁偶极矩:

因此,在施加磁场(顺磁)后,它会自行定向。从量子力学可知,除了角动量L之外,亚原子粒子还具有固有的角动量或自旋。自旋与磁偶极矩相关联,如方程(1)所示,前提是方程(3)中的比例系数发生改变。即使是核自旋,在施加外部磁场后也会倾向于自行定向。在最简单的情况下,根据自旋角动量指定方向的分量只能有两个值(大小相等但符号相反),因此只有两个可能的方向。这就是电子或所谓的自旋1/2系统的情况。假设原子核/离子在晶格节点中静止,我们就会发现唯一的自由度是表达与外部磁场相互作用的自由度,这些自由度由势能项描述。在自旋为1/2的原子核系统处于静态均匀磁场B0中的特殊情况下,我们最终得到两个能级:基本能级(即最小能量)对应于沿B0方向定向的磁偶极子,以及偶极子沿相反方向定向的激发能级。由于系统倾向于占据最小势能状态(“人口最多”),因此基态能级上的原子核数量预计会非常多。
如果我们瞬间反转磁场B0(将磁铁旋转180°)会发生什么?基本能级会变为激发能级,反之亦然,因为在新的磁场配置中磁偶极子的方向相反。这是非典型的,因为基本能级现在“人口最少”。量子统计力学通过倒置绝对温度的符号证明了这一点。然而,经典统计力学也提出了同样的结论。事实上,如果我们看一下玻尔兹曼统计分布:

其中kB是玻尔兹曼常数,A是归一化常数。我们发现,能量越高的激发能级越不容易被占据,因为T>0。因此,倒置符号是一种数学手段,用于证明所谓的反常的物理现象,因为T<0的热力学状态是亚稳态的:系统倾向于恢复T>0。T<0状态的另一个奇怪特征是内能大于T>0的状态。前者通过让T<0的物体与T>0的物体热接触,每秒都在传导能量。换句话说,T<0的物体比T>0的物体更热。对于上述情况,如果我们理想晶体的原子核/离子系统是自旋1/2系统,通过施加磁场B0,我们可以得到如图2所示的能级分布。
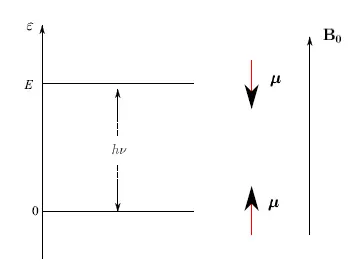
图2:能级分布
磁体的瞬时旋转会引起粒子数反转,从而形成T<0的亚稳态。这样,核自旋系统就会向晶格释放一定量的热量。图2显示,能级之间的差值为hν,其中ν是具有量纲的频率。该差值与B0成正比。从数量上讲,这相当于发射频率为ν的光子,对于适当的B0值,该光子属于可见光谱。理想情况下,我们制造的LED位于可见光谱内,具有合适的B0值。不幸的是,石墨烯并不适合这样的实施方案,因为碳原子核的自旋为零。然而,如果我们采用它的重非放射性同位素Carbon-13(13C),我们就会发现,根据众所周知的核物理规则,其原子核的自旋为1/2,因此它似乎是理想的候选物质。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Behavior of Isotopically Modified Graphene,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯