
在上一期中,我们用重同位素13C取代了单个碳原子,对石墨烯进行了虚拟改良。这样就可以验证,在(静态)磁场B0发生"翻转"后,与单个原子核自旋磁化相对应的原子核能级存在粒子数反转。由此产生的“弛豫”过程伴随着量子力学规则下电磁能量量子的发射。所有这些都是在玻恩-奥本海默近似下进行的。
在本期文章中,我们将对原子核的运动(晶格振动)进行定性分析。由于热扰动,这些是围绕平衡位置(晶格节点)的“小”振荡。量子力学需要对这些振荡进行量子化,就像空腔(黑体)内电磁场的振荡一样。众所周知,在后一种情况下,量子化导致产生了光子的概念。同样,晶格振动场的量子化也会产生所谓的声子。如果我们考虑到波粒二象性,这个结论就不会令我们感到惊讶。
这些论据让我们猜想,与磁场B0平行的磁矩发射的是声子而不是光子,它们在B0反转后占据了激发能级。实际上,我们正面临着固态理论物理中的一个难题,因为晶格是一个由相互作用的磁荷和偶极子组成的复杂系统。因此,很难预测磁矩能量是如何在激发能级释放的。这种能量会转移到晶格加电子系统的自由度上,但并不是说这些自由度一定具有声子性质。
然后是13C的问题,它是12C唯一稳定的同位素,核自旋为1/2。不幸的是,与12C不同,这种同位素在自然界中分布很少(1.11%)。不过,该同位素可以作为杂质引入类石墨烯结构中,然后通过上一期提出的实验来研究其行为。石墨烯-Si/Ge/SiC/GaN结型异质结构的实现似乎也很有可能。
现在让我们来看看12C和13C之间的区别。作为同位素,它们具有相同的电子构型,用光谱符号表示可以写成如下:

等式(1)可以解读如下。12C/13C原子中有六个电子:两个处于基本能级(根据泡利不相容原理,具有反平行自旋),四个处于激发态第一能级。考虑到轨道角动量的自由度(从技术上讲,我们谈论的是轨道角动量的本征态/本征值)和自旋,我们得出结论,要完成外轨道,还缺少四个电子。因此,每个电子将与相邻原子的相应电子键合(共价键)。关于12C的原子核结构,我们有六个质子和六个中子。根据众所周知的核物理规则,12C的原子核自旋为0。很明显,通过“添加”一个中子,新的原子核将具有1/2的自旋,因为这是中子的自旋。
让我们考虑一下图1的方案,其中D1(光电二极管)和D2(LED)串联在一起。准确地说,D1的阻断迫使发生器提供由下式给出的电流值:
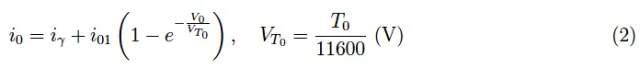
假设V0<VZ(D2)=D1的电压。这里T0是室温,而i01是D1的反向饱和电流。D2两端的电压降由后者的电压-电流特性计算得出:

其中i01是D2的反向饱和电流。
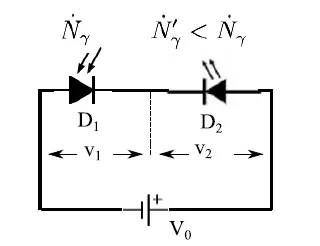
图1:由光电二极管供电的LED
因此,D1两端的电压降为:

电流i0决定D2中的电荷注入,从而使D2发出红外线。我们不能将其与焦耳效应引起的热发射混为一谈,因为LED使用的是不同的物理过程(如之前的教程中所示)。根据韦恩定律,将LED的发射光谱近似为黑体的发射光谱:

其中T>T0是LED吸收能量后达到的温度,而λ0是发射辐射的主波长。由于方程(5)中的二元常数已知,我们可以通过测量T来知道发射波长(预计在红外波段)。LED的效率定义为输出辐射功率与输入辐射功率之比:

在入射光子通量相同的情况下,发射光子的通量取决于i0,因此也取决于V0:
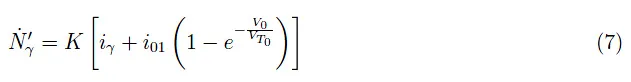
K>0是一个比例系数,我们可以将其视为常数。锗二极管的一些典型值如下:
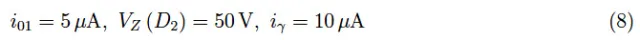
将在K上归一化的方程(7)绘制出来,我们得到如图2所示的结果。由此我们可以看出,LED发出的光通量与V0关系不大。
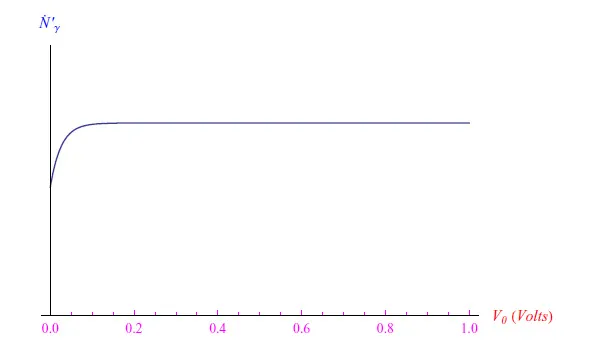
图2:LED发出光子的通量趋势
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: the ‘photoLED’,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯