
在上一期工作中,我们研究了作为电路非线性元件的二极管的混沌行为。在本文中,我们将讨论与半导体中特定电荷分布相对应的量子混沌。
首先我们介绍一些相关的基本概念。在量子力学(QM)中,不受作用力的粒子(例如电子)由单色平面波来描述,其中传播矢量(波矢量)和角频率分别由下式给出:
 其中:k=h/2π是普朗克约简常数(h=6.6260755×10−34J·s是普朗克常数);p是动量,E是能量。
其中:k=h/2π是普朗克约简常数(h=6.6260755×10−34J·s是普朗克常数);p是动量,E是能量。
值得注意的是,在这样的量子态中,由于没有外力作用在系统上,因此能量是确定的并且是恒定的(上述量子态称为稳态)。然而,QM的线性也意味着态叠加原理的有效性。在我们研究的案例中,这是由平面波的干涉产生的,平面波的干涉返回一个在非常小范围内的波包,以这种方式很好地代表了一个点粒子。在这种位形中,能量是不确定的:只有在测量之后,波包才会被减少到测量能量值所对应的单色分量。这个过程被称为波包(或波函数)坍缩。这是QM早期引起争议的根源,因为这种减少并不是一个确定的过程,而是一个随机的过程。
有趣的是,在两种位形(平面波、波包)中,电子的能量都没有被量子化。准确地说,我们有:
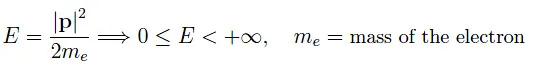
与之相反的情况是,电子被限制在有限的空间区域内。在这种情况下,我们必须讨论波动力学,因为我们有一个正在传播的波,无论是平面波还是波包。因此,我们预计会有驻波的出现,即出现没有传播特性的波。用一个简单直观的例子来形象化这种现象,假如一个摩托车手在两侧高楼林立的街道上高速行驶,其带来的发动机轰鸣声会激活停放在道路两旁的车辆警报器,在这种情况下,我们就产生了声波。而用以描述它们的数学方程实际上是相同的(尽管电子的波动方程是薛定谔方程而不是达朗贝尔方程),它们从建筑物的墙壁反射,产生相长干涉。其结果是形成了一种不传播但仍具有振荡特性的波。有趣的是,驻波的频率构成了一个离散的频谱。将这一论点转移到量子领域,我们立刻就会发现,在电子被限制在有限区域内的情况下,能量谱是离散的或量子化的。
更具体地说,电子的限制是通过一个无限高的势垒来建模的,在半导体中,可以通过晶格节点中“固定的”离子电荷的特定分布来创造。然而,这就意味着存在一个没有固定电荷的区域,在这个区域中,电荷载流子(电子和空穴)的行为就像自由粒子一样,会与“墙”发生弹性碰撞 (已知的是,如果我们考虑粒子行为,它与波状的行为同时存在)。因此,在载流子被限制在没有固定电荷的有限区域内的情况下,我们预计能级E1、E2、…、En、…会离散分布。
请注意,这些是单个粒子的能级,要得到总能量,就必须知道统计分布函数,对于室温下的半导体来说,该统计分布函数是玻尔兹曼分布。因此,我们看到的在结晶固体(导体或半导体)中移动的电荷载流子的行为存在偏差,这种结晶固体的理想状态是点阵,单个离子位于其晶格的节点上。众所周知,在后一种情况下,单个电荷载流子在势能力场中运动,而势能力场是空间坐标的周期函数,具有与晶格相同的周期,即a(=晶格间距)。
从量子角度来看,稳态是是振幅受周期为a的周期函数调制的平面波(布洛赫波)。通过求解稳态薛定谔方程,可以发现对于这个特定的量子系统,能谱分布在带状或连续的间隔内,并由间隙分隔开。在半导体的特殊情况下,价带(束缚载流子)与导带(自由载流子)之间存在禁带,该禁带可以通过热能来克服。
经典粒子被限制在一个具有椭圆边界的平坦区域中,这种情况非常有趣。我们可以想象一个"椭圆形"台球桌,其边缘恰好是一个椭圆。在球与台球桌边缘完美弹性碰撞的理想情况下,机械波的反射定律成立:球直线轨迹撞击边缘的入射角等于相应的反射角。排除周期性轨迹(如果初始位置是椭圆的两个焦点之一),这种特殊的机械波系统已被证明对初始条件具有敏感的依赖性。更具体地说,碰撞产生的轨迹很大程度上取决于迎角。后者的微小变化都会对轨迹产生巨大影响。从技术上讲,该系统受到了确定性混沌的影响。从本质上讲,尽管系统是确定的(因为它遵循经典力学),但它具有不可预测的动态演化。
量子领域是否也存在类似的过程?答案是肯定的:M.Berry证明了一类特定的量子力学系统存在混沌行为,而使我们感兴趣的是这同名的台球系统。该系统可以对上一期文章中定义的边界区域的拓扑进行建模。
在贝里的台球中,单个粒子的能级是根据黎曼zeta函数零点的虚部排列的,该函数是一个复变函数,其行为与素数的分布有关。根据黎曼假设,这些零点属于复平面的直线,方程为Re s=1/2(临界线),其中s=ξ+jη是通常的复变量,j2=−1。这些零点组成了一个可数的无限集。考虑到它们在复共轭下是不变的,即分布与实轴对称,图1突出显示了其中的部分零点。不过,我们只对那些具有正实部的粒子感兴趣。在贝里的台球中,第n个零点的虚部ηn是无量纲单位中的第n个能级。换句话说,它必须是En=kΩηn,其中Ω>0是一个具有频率量纲的合适常数。
零点似乎聚集在临界线上,即En+1−En的差值似乎随着n的增加而减小。事实证明,零点往往会相互排斥。
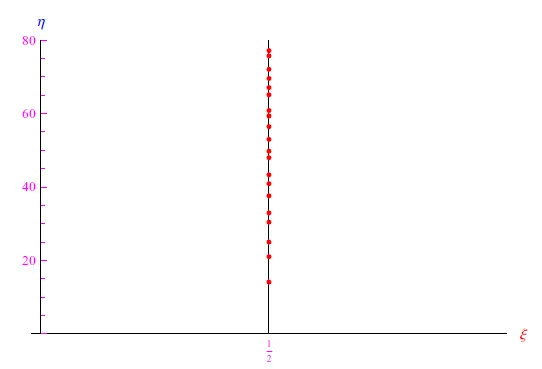
图1:黎曼zeta函数的一些零点
由“距离”u分隔的零点对的相关函数如图2所示,从中我们可以看到,更有可能找到“远”零点对。
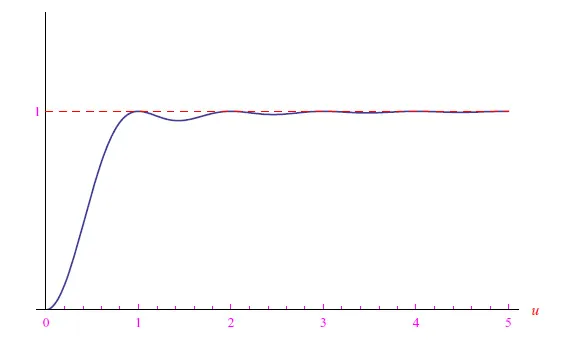
图2:由“距离”u分隔的零点对的相关函数
因此,我们距离表征更简单(且有序)量子系统(例如谐振子)的均匀能级间距还很远。然而,氢原子的能级中却发现了均匀性的损失。不过,在这种情况下,能级趋于增厚,并且不会像贝里的台球那样相互排斥。据推测,这是由量子混沌造成的。
在室温下的未掺杂半导体中,电子和空穴在“能量上”相距较远,因为前者位于导带,而空穴位于价带(因此能量较低)。如图3所示,两个能带被禁带εg分开,电子利用热能克服这个禁带。不过,这些电荷载流子“物理上很接近”(重组过程就是基于这种接近)。
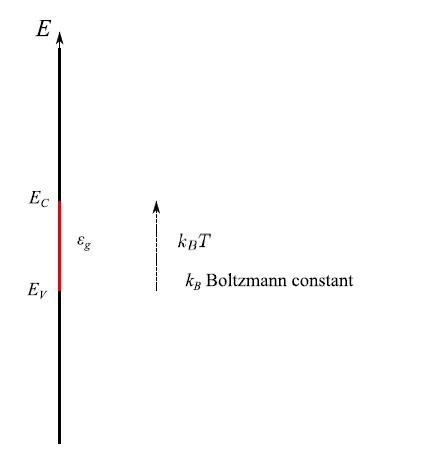
图3:未掺杂半导体中的价带和导带
在掺杂半导体中也会出现的一个基本问题是单带能级的连续性。如上所述,在室温下,玻尔兹曼分布(经典统计力学)给出了能级的统计分布。不然,由于电子浓度太高,费米温度TF=EF/kB与温度环境处于同一数量级,金属会发生简并化。回想一下,费米能量EF是在绝对零度下占据的最高能级的能量,根据泡利不相容原理,单个量子态最多可以被两个电子占据,一个电子自旋向上,另一个电子自旋向下。可以通过人为增加载流子(电子和空穴)的浓度来调节统计分布。然后费米-狄拉克统计将描述该系统,从而导致简并化。在这种情况下,半导体被称为简并半导体。
如此前文章所述,在具有耗尽层(DL,其中仅存在电子)的半导体中,相应的能级被量子化。由于不相容原理,单个能级最多可以被两个电子占据,这与没有DL的半导体的情况完全相同,不同之处在于现在能级被量子化。如果N≫1是电子总数,那么我们可以得出,电子的分布可以填充单能级,直到Emax=[N/2],其中[·]表示整数部分。Emax相当于简并电子系统的费米能。
我们得出的结论是,如上一节所述,具有DL的半导体可能会表现出反常行为。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: the Quantum Chaos,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯