
在上一期的文章中,我们了解了光电导体是如何得到截止波长的。而这严重限制了辐射计(即基于光电导体的辐射探测器)的使用。截止波长通常出现在远红外光谱中。对于更长的波长(红外线、微波),则需要使用热探测器(测量温度变化的设备)。可以想象,半导体由于具有敏感的温度相关性也被应用于此,其中就包括辐射热计。
图1显示了半导体低温辐射热计的热力图。由于偏置电路,电流i流过半导体。其中R是半导体本体的电阻(不要与动态电阻或微分电阻混淆),由于焦耳效应,它会消耗功率W。器件所处的环境会产生功率为Wγ的辐射背景。半导体通过导热系数为G的金属线与低温恒温器(T0接近绝对零度的恒温器)保持热接触。正如我们将看到的,极低的温度(通过低温技术达到)对于降低热噪声至关重要。此外,要测量温度波动,还必须有一个稳定的热基准T0,这与使用半导体时的情况不同,因为半导体体积小,热容量低。
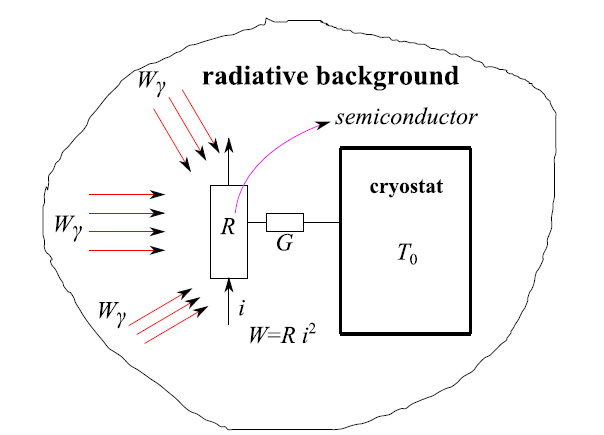
图1:半导体低温辐射热计的热力图
相应的电偏置电路如图2所示。低噪声电池提供电压V0,相应的电流如下:

其中RL是负载电阻。输出电压由下式给出:

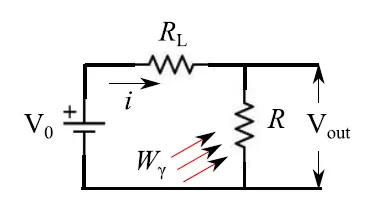
图2:半导体低温辐射热计的电气原理图
辐射热计的工作原理非常简单。因为在半导体中,R=R(T),即电阻取决于工作温度,并且入射辐射功率的变化δWγ(可能由于热源引起)决定了电阻的变化δR随后续温度的变化δT而变化。通过R对方程(2)微分,经过一些步骤,我们得到:

其中:

方程(3)表示输出电压波动(待测信号)与温度波动之间的联系。要使δVout(其在任何情况下都必须放大) 达到一个较好的值,我们必须最大化无量纲参数F(即F≃1),这适用于负载电阻RL≫R的值。
以更简洁的形式重写方程(3),我们有:

在这里我们看到,除去一个不重要的比例因子K,测量δVout相当于测量由于入射到辐射热计上的辐射功率的变化δWγ引起的温度波动δT。
我们使用了一个200µm的立方体锗样品,并配备了蓝宝石作为辐射吸收器。低温恒温器(氦3)的温度为T0=0.3K。
回想一下之前所介绍的,在绝对零度的情况下,任何半导体都是绝缘体。与温度变化δT相对应,跳跃电导被激活,而其他传导模式被“冻结”。然而,在[0,δT]范围内,电导率仍然很低,并且半导体本体的电阻R相对较高(在我们的例子中,R=1MΩ)。随着温度升高,电导率增加,因此R减小。换句话说,在低温范围内,dR/dt<0且α<0。这表示为半导体低温辐射热计为负值。在本例中:α=-10K-1。
根据上述内容,我们使用了高负载电阻(R),从而获得F=1,偏置电位可产生i=1nA。
用于校准气泡计的操作上有用的量是响应度:

这可以通过测量已知光源(例如黑体)的δWγ产生的δVout来确定。由于很难在红外波长下制造这样的光源,因此我们更倾向于确定电响应度。大体上,我们考虑的是一个具有发射光谱的虚拟光源,其产生的(δWγ)(t)可分解为正弦基本振荡,即可在傅里叶积分中展开:
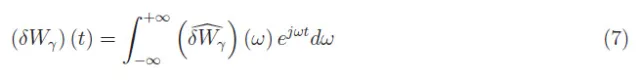
其中:
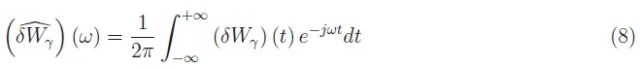
是(δWγ)(t)的傅里叶变换。
现在让我们继续看图1的热力图。下面的稳态方程描述了处于平衡状态的背景+系统+半导体+低温恒温器:

其中T>T0为平衡温度,Gs为稳态热导率。波动δWγ决定了温度波动δT,同时由于焦耳效应,半导体耗散的功率δW会进一步变化。这些变化显然是时间的函数,因此我们将在下面使用学术但明确的符号来描述:

由式(9)我们可以写出:
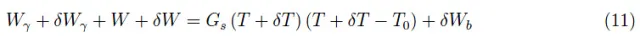
其中δWb是半导体热容量的影响(很小,但不为零):
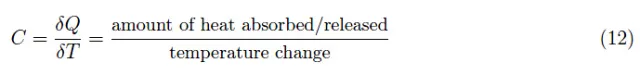
之后:

得到焦耳效应引起的变化δW后代入式(11),计算后得到辐射热计的方程:
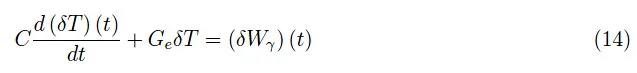
在中间步骤中,我们首先引入动态电导率:
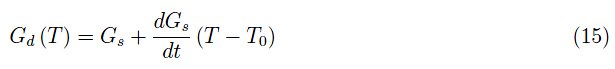
因此,有效电导率:
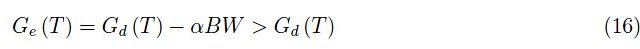
因为辐射热计为负值。该结果具有以下物理解释:α<0改善了半导体与低温恒温器之间的热接触,因为-αBW>0会增加动态电导率。我们将αBW称为电热相互作用项。我们注意到,由于α<0,当δW>0时,温度升高,因此R和耗散功率W会降低。
方程(14)是一阶线性常微分方程。考虑到方程(7),并展开傅立叶积分求出一般解,我们得到:
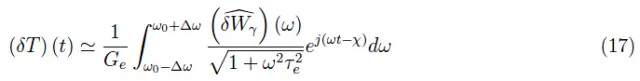
其中,我们考虑了主频率ω0周围的峰值谱密度。相对于辐射源的相应傅立叶分量,各个傅立叶分量的相位相差一个角度χ=arctan ωτe。由此可见,量τe=C/Ge定义了辐射热计的响应时间。这可以解释为一个时间常数,因为τe定义了一个注定会消失的瞬态项。这种行为是由线性非齐次ODE所表示的动力系统的特征。对于辐射热计,根据参考文献中证明的定理,我们有:

由于瞬态项是exp(−t/τe),因此它呈指数递减。简而言之,对于t≫τe,辐射热计会“即时跟踪”辐射功率的波动。这就是为什么我们需要最小化τe的原因,否则,这个器件就会变得“缓慢”。从方程(18)我们看到,为了获得可测量的δT,我们必须最小化Ge。由于这相当于增加响应时间τe,因此我们必须寻找一种折衷的方案。在我们的实验中,我们有:
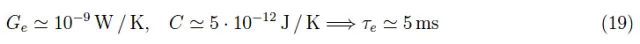
备注:在此框架中,辐射热计属于此处描述的动态系统类别。
我们获得的结果使我们能够定义光谱响应度:
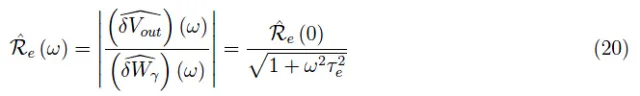
其中:

从上式可以看出,我们必须使用低导电率的热导体才能获得明显的响应度。然而,这会增加辐射热计的响应时间。这印证了前面关于需要寻求折衷方案的论点。影响响应度的其他参数包括偏置电流α和电阻R。不建议过多增加电流和R,因为这会增加噪声。
在操作上,我们采用了与上一问题相反的过程,即根据给定的δWγ(在任何情况下都无法通过傅里叶积分表达)确定δT。现在,通过测量δVout=KδT,我们必须“重建”辐射信号δWγ。为此,我们为辐射热计配备了一个电动机,使器件绕垂直轴(天顶)旋转。来自偏置电路的信号δVout经过放大(通过低噪声放大器)后,通过软件(Octave)以.dat文件格式获取,然后在Mathematica计算环境中重新处理。准确地说,通过插值指令我们得到了一个函数δT(ρ,θ,t),其中(ρ,θ)是器件所在点与地球表面相切平面上的极坐标。具体来说,其范围是:

其中ρmax是最大距离,这取决于空气湿度,因为水蒸气分子会强烈吸收红外线。例如,在雨天,ρmax=0。部分结果如图3所示。
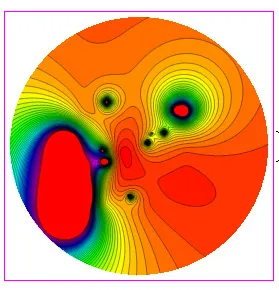
图3:红外测绘
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Semiconductor Cryogenic Bolometer,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯