
众所周知,半导体在绝对零温度下是绝缘体。在0<T<1K范围内,由于掺杂而产生的电导模式会被激发。我们特别要提到的是跳跃电导,这是一种复杂的量子机制,即使在低温下也能保证导电性。在高浓度的受体/供体掺杂下,原子间距离会变小,使得单电子/空穴布洛赫波函数从一种杂质延伸到另一种杂质,从而提高电导率。
泡利不相容原理也起着重要作用,因为它决定了单个电荷载流子能级分开。其结果是能级呈连续分布,形成一个个能带。显然,这是一种难以控制的传导模式,但仍然具有优势,因为它保证了半导体在一定温度范围内的导电性,而在这个温度范围内,所谓的典型模式是"冻结"的。半导体电阻与温度(接近绝对零)的函数的经验关系如下:

其中A>0是一个常数,与Tλ在同一范围,λ>0取决于掺杂类型。该指数可取1、1/2和1/5值。进行锗掺杂以触发跳跃电导的有效方法是中子嬗变:将晶体浸入由核反应堆产生的热中子浴中。中子被锗吸收,并在随后的化学过程中形成高浓度的杂质,其行为类似于受体/供体。
式(1)中R∞理论上是R(T)的渐近值;实际上,该公式仅在接近绝对零度的短范围内有效。对于中子嬗变,它是λ=1/2。通过为方程(1)的常数赋予合适的值,我们可以得到与R(T)的导数成比例的参数α。这是一个重要的参数,因为它量化了半导体对温度变化的“响应”。
在上一期介绍的实验中,我们测量了δVout,然后通过温度变化δT重建了入射辐射功率。信号δVout不可避免地会受到噪声的影响,因此我们可以写:

用N表示噪声,其由多个项组成:

其中NJ和Nshot分别是约翰逊噪声(热噪声)和散粒噪声,已在之前的工作中进行过研究;N1/f是1/f噪声(闪烁噪声),似乎不仅存在于半导体和金属中,甚至在生物结构中也存在。顺道一提,在大脑的生物电曲线中也观察到了这种噪声。这种噪声很难处理,我们只能观察到它的功率谱与频率的倒数成正比,因此它在低频时占主导地位,并且与温度无关(就像散粒噪声一样,但它是白噪声)。
所谓的热电效应限制了半导体辐射热计中的约翰逊噪声。当该噪声引起正波动δVout时,半导体升温,因此电阻R减小(参见上一期内容)。这种情况使得高压波动的可能性降低。类似的论点也适用于δVout<0的情况。
在Mathematica计算环境中,可以再现白噪声和所谓的布朗噪声(又称棕色噪声或红噪声)。对于白噪声(用y表示),我们首先生成一个遵循高斯分布的随机数数组,并指定其方差和均值(可以通过重新定义缩放因子将均值设置为零)。图1显示了白噪声的典型模式。
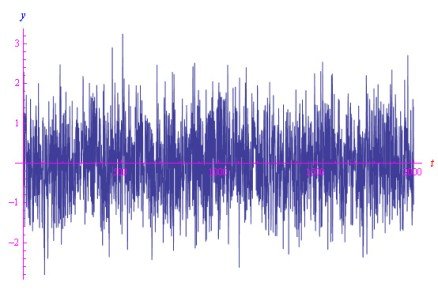
图1:白噪声
通过插值指令处理白噪声数组,Mathematica返回一个完整的函数(数学分析中的函数)。这个过程的优点是显而易见的,因为函数是比数组更易于管理的对象。这样的函数在其定义集的每个点即每个时刻,都具有有限的不连续性。即使是为这个特定的分布分配的,不连续性跳跃也是随机的。通过生成一个新的随机数组,我们可以得到一个新的分布,从而获得新的函数。然而,以这种方式生成的函数是病态的,因为它们在每个点上都有不连续性,并且基本上无法表达。不过,通过Integrate指令,我们可以计算出一种称为布朗噪声的基元,其图形如图2所示。
如图所示,白噪声随时间变化的值是100%不相关的。用τ表示给定的时间间隔,我们得到y的自相关函数:ϕy(τ)=Aδ(τ),其中δ(τ)是狄拉克δ函数。根据维纳-欣钦(Wiener-Kintchine定理),y的功率谱wy(f)是自相关函数的傅立叶变换,而这是一个狄拉克δ函数,它遵循wy(f)=A。因此,白噪声的功率谱是平坦的这一众所周知的结果得到了证实。在实际操作上,频谱会表现出截止频率fmax,其中当f>fmax时wy(f)=0。
现在让我们看看如何从采样值数组开始重建自相关函数。通过对采样数据(数组)执行DFT/FFT处理,我们可以在Mathematica中定义一个相关函数,其参数是不同的数组(例如,两个数组一个可以是白噪声,另一个可以是棕色噪声)。通过叠加参数,我们可以获得给定噪声的自相关函数。
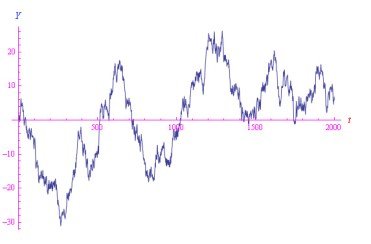
图2:布朗噪声
例如,对于白噪声,我们得到如图3所示的图形,而对于棕色噪声,我们得到如图4所示的图形。
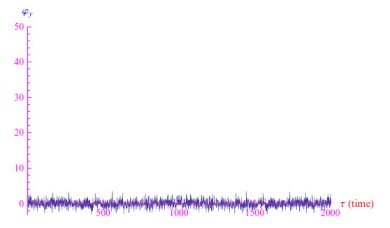
图3:白噪声的自相关函数
该过程的计算优势在于,可以将插值获得的函数假设为微分方程中的已知项,从而获得随机微分方程(SDE)。例如,众所周知,随机移动类型的微分方程返回棕色噪声。
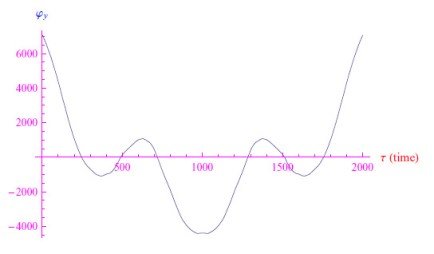
图4:棕色噪声的自相关函数
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: hopping conduction and X-Noise,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯