
尽管无源PWM DAC纹波滤波器有使用局限,但其简单和低成本优势使得它很受欢迎。这些限制之一是由滤波器电阻(图1中的Rf,每个级联滤波器RC级对应一个电阻)串联引起的高输出阻抗,这使得整体DAC精度对输出负载非常敏感。设计人员的手段是使Rf尽可能低,除非他们想要诉诸有源输出缓冲,但这样会失去一些PWM的简单性和廉价性。
那么,有多不实用,以及有哪些因素会造成限制呢?
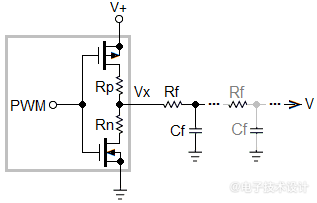
图1:一种通用无源PWM滤波器拓扑,每个级联滤波器RC级都有一个电阻器(Rf)。
尽管纹波滤波器可能包含多个级,但第一级通常是“能降到多低”的决定性因素,原因如下:
1.在几乎所有(甚至多级)纹波滤波器设计中,如果有后续级的话,那其Rf与第一级的Rf成正比。因此,当已知第一级的Rf时,它们的值以及最终的DAC输出阻抗也是已知的。
2.为了更好地近似,完整的峰峰值V+ PWM波形幅度通常出现在第一级Rf上,因此功率和电流消耗等实际限制因素几乎完全由其电阻决定。最坏情况下的平均功率和电流消耗通常发生在50% PWM占空比或其附近时,计算公式为:
Imax=V+/(4Rf+2Rn+2Rp)
Pmax=V+2/(4Rf+2Rn+2Rp)
其中,Rn是N沟道开关的导通电阻,Rp是P沟道开关的导通电阻。
假设选择10mW作为最大滤波器功耗,并且V+=2.5V,则滤波器输出阻抗由下式给出:
Z10mW=Rf+(Rp+Rn)/2=2.5V2/10mW/4=156Ω
所得到的156Ω是一个非常低且负载耐受能力强的输出阻抗(能够在40k负载电阻下保持8位精度),并且实际上类似于零电压输出饱和时轨到轨缓冲运算放大器的阻抗。为了进行比较,可考虑代表性的RRIO运算放大器(TLV237x),其在灌电流1mA时保证的最小输出V为150mV,转换为等效阻抗为:
0.15V/0.001A=150Ω
请参阅“TLV237x-Q1 550-µA/Channel, 3-MHz Rail-to-Rail Input and Output Operational Amplifiers”(TLV237x-Q1 550µA/通道、3MHz轨对轨输入和输出运算放大器)第8页的低电平输出电压。
当Z=156Ω时,纹波滤波器在某些电路状态下几乎与缓冲输出一样好。对于简单、廉价的无源滤波器来说,这样的性能出人意料。但它最终实用吗?上面的计算隐含地假设Rn=Rp。如果不是这个关系,如图2中用于生成精密2.5V PWM波形的TMUX4053开关的导通电阻(Ron)与源极或漏极电压(V)关系图所示,会发生什么情况呢?
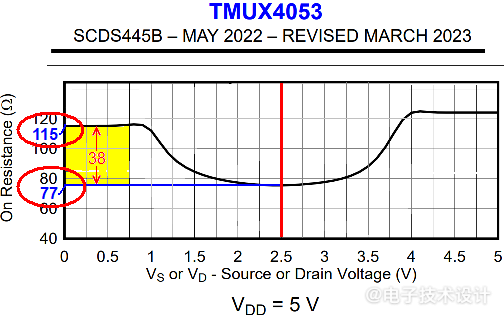
图2:25℃时Rp和Rn不相等的TMUX4053的导通电阻与源极或漏极电压的关系。
25℃时,Rp为77Ω,Rn为115Ω。如果令:
Rf=156–(Rp+Rn)/2=60Ω
则为滤波电容器充电的净电阻:
Rf+Rp=60+77=137Ω
明显小于放电电阻:
Rf+Rn=60+115=175Ω
其对称因子为:
S=(Rf+Rp)/(Rf+Rn)=137/175=0.78
不幸的是,虽然可以最小化输出阻抗,但如此大的上/下电阻不对称性对于DAC积分线性度来说是一件坏事。图3显示了S=0.78对线性度的影响:与精确线性度的满量程偏差超过6%。
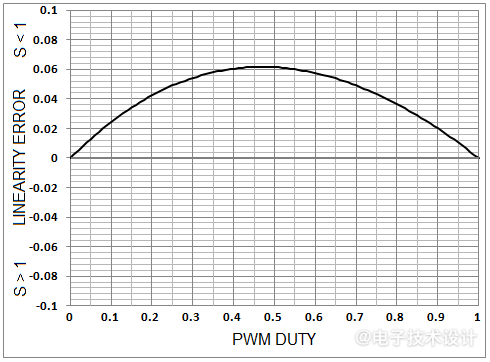
图3:线性误差与PWM占空比的关系,其中S=0.78会产生约6%的积分非线性。
其实,这是一个普遍的结果。对于所有给定的S,可以预期积分非线性度约为:
INL~(1–S)/4
且S<1时线性偏差为正,S>1时线性偏差为负。
因此,如果想要abs(INL)=2-9实现可靠的1/2 LSB 8位线性度,则需要:
abs(1–S)=4×2-9=2-7
对于所考虑的示例:
(Rf+Rp)/(Rf+Rn)=1–2-7=0.9921875
Rf+Rp=0.9921875Rf+0.9921875Rn
(1–0.9921875)Rf=0.9921875Rn–Rp
Rf=4749Ω
因此,输出阻抗必须增加30倍至4.8kΩ,才能恢复8位线性度,从而使8位精度的最小负载约为1.2MΩ。
那是否有简单、廉价的解决方案,可解决这个严重弯曲的线性问题呢?
事实上是有的。以下是简单的计算校正过程:
1.令Vo=所需的DAC输出。
然后,不要按照惯例将PWM占空比设置为T=Vo/V+,而是将T*替换为:
2.T*=T/(T+(1–T)/S)。
然后,只要为S提供准确的值,积分线性度就会恢复。不幸的是,简单地根据开关数据手册中的典型Rn和Rp数字计算S值可能不够准确。最好(也许是强制性的)直接测量所使用的实际器件的S值。但如何测量组装电路中的Rn和Rp呢?
下面这种简单的在电路方法无需费心去测量内部开关电阻:
1.设置PWM占空比=0.5=50%;
2.用高阻抗电压表读取Vo和V+;
3.然后就可以将S值计算为S=(1–Vo/V+)/(Vo/V+)。
因此,通过这种一次性电压测量和简单的基于软件的校正,上面计算出的最小输出阻抗与8位DAC线性度兼容,并且最终能够实用。
这意味着输出阻抗确实可以降到那么低,而不需要用到运算放大器。
(原文刊登于EDN美国版,参考链接:Minimizing passive PWM ripple filter output impedance: How low can you go?,由Franklin Zhao编译。)
本文为《电子技术设计》2023年10月刊杂志文章,版权所有,禁止转载。免费杂志订阅申请点击这里。
 最前沿的电子设计资讯
最前沿的电子设计资讯