
在本文中,我们将探讨信号的谐波失真分析、测量和仿真。当电信号通过设备或电路发送时,会失去或改变其初始特性,产生谐波失真。这种类型的失真会导致信号中出现谐波,而谐波是频率为基频倍数的正弦分量。设计人员的主要目的是消除或尽量减小失真的程度。
谐波失真可能发生在任何信号频率上,并且可能由许多不同的因素引起,包括:
谐波失真会对信号质量产生负面影响。它降低了信号的保真度和质量,大大降低了准确呈现原始信号的能力。此外,谐波失真还会导致各种技术问题,例如噪声增加和设备异常发热。测量信号的谐波失真需要使用非常精密的测量仪器。如果掌握了各种谐波的振幅,则可以进行手动计算。总谐波失真(THD)通常是通过将基频的前五次或六次谐波的平方相加来计算的。然而,在许多实际情况下,即使只包括第二次和第三次谐波,误差也可以忽略不计。谐波失真率的计算公式如下:
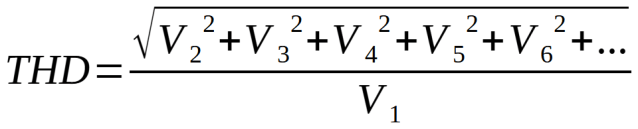
其中V1是基频的幅度,V2是二次谐波的幅度,V3是三次谐波的幅度,依此类推。
如果需要百分比形式的值,只需将结果乘以100。从公式中可以很明显的看出,如果信号中没有谐波,则分子等于0,THD值也等于0。图1显示了一个周期信号的例子,该信号是晶体管过度放大的结果。信号肯定是失真的,通过观察波形图也可以理解。放大电路使用的晶体管连接到共发射极,具有可控增益,产生的输出信号放大了约7倍,与输入信号反相。
出现失真有三个原因:
图1显示了以下部分:
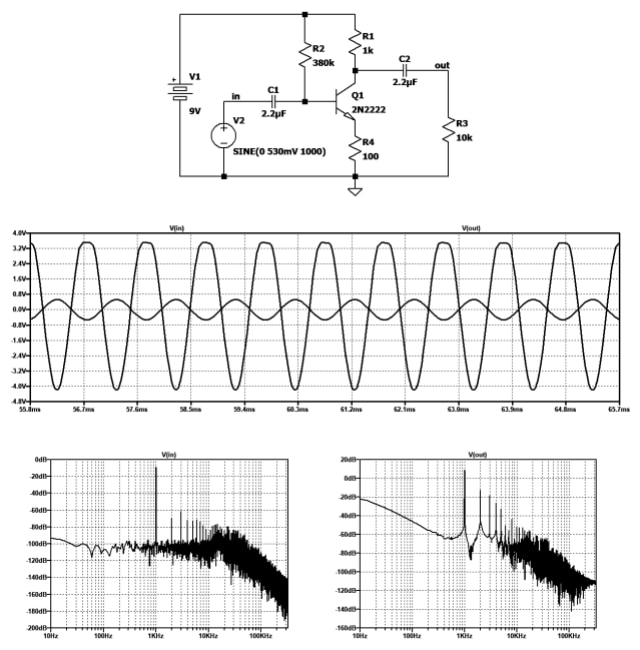
图1:晶体管放大器可以放大信号,但不可避免地会造成或大或小的失真。
现在可以手动计算输入信号的失真,理论上该信号应该是纯净的。仅考虑以下谐波的振幅(RMS):
六个谐波对于手动计算来说绰绰有余。可以利用上述公式计算出THD值:

如果您想要百分比形式的值,只需将结果乘以100,在这种情况下,输入信号的谐波失真为0.269%,这是一个相当纯净的值。现在,您可以手动计算失真输出信号的失真度。此外,在这种情况下,我们仅考虑以下谐波的振幅(RMS):
同样,六个谐波对于手动计算来说绰绰有余。可以利用上述公式计算出THD值:
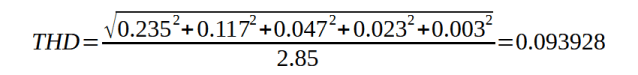
如前所述,如果您想要百分比形式的值,只需将最终结果乘以100,在这种情况下,输出信号的谐波失真为9.3928%,这对于任何类型的应用来说都是不可接受的值。
作为手动计算的替代方法,可以使用LTspice进行谐波失真计算,对电路进行建模并观察其对输入信号的影响。电路建模完成后,就可以使用以下指令来仿真其对正弦信号的响应:
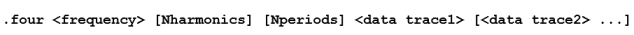
回到我们的电路,也是为了确认之前的手动结果,我们希望LTspice能够计算输入信号和输出信号的失真。因此,有必要在电路图中插入以下指令:
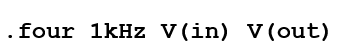
分析的频率必须与电路信号发生器的频率相匹配,在本例中为1,000Hz,即基频。执行瞬态分析后,结果显示在“Spice Error Log”窗口中,也可以通过按CTRL+L键激活该窗口,如图2所示。最终结果与手工计算结果相差不大。前九次谐波的THD值已计算完毕,结果显示在分析的最后。信号所有谐波的结果也显示在括号中。
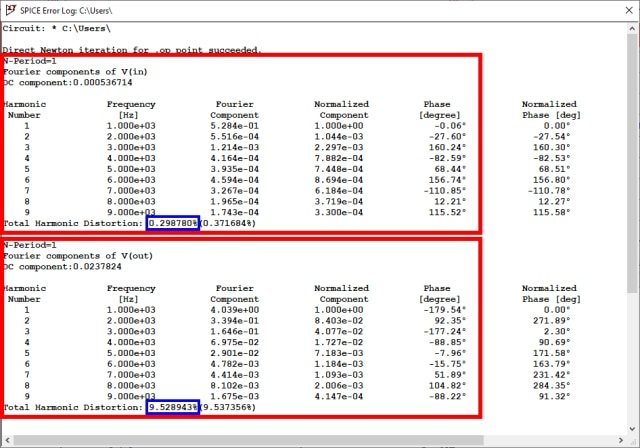
图2:使用LTspice可视化信号失真值
即使使用ngspice,谐波失真的计算也非常简单。为此,在这种情况下,用户必须在系统提示符下以批处理模式运行软件,命令如下:
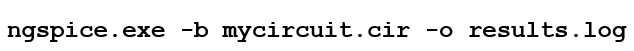
包含电路描述以及指令的SPICE脚本如下:

图3显示了包含ngspice谐波失真分析结果的报告。它们与LTspice计算的结果非常相似,但由于算法不同,因此不可能完全一致。ngspice所考虑的谐波次数与其他软件相同。
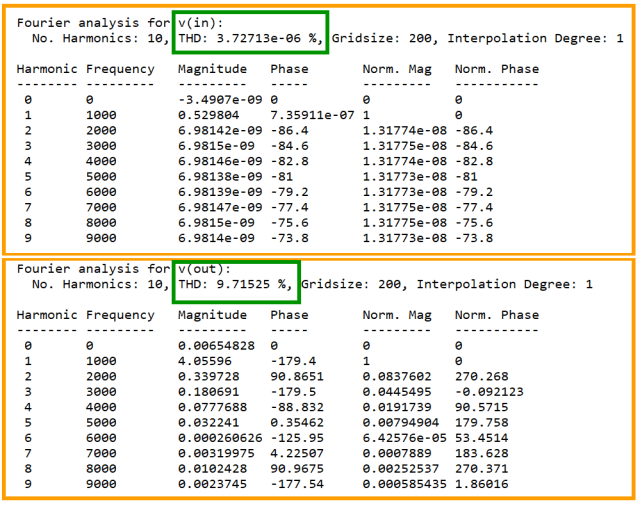
图3:使用ngspice可视化信号失真值
下表显示了对于示例电路的信号谐波失真百分比的汇总。手动计算是使用仿真频谱分析仪进行的,但所使用的三种方法的失真百分比最终值非常相似。

仿真程序是研究谐波失真的一个很好的工具。利用它可以进行快速、准确的仿真,而无需构建设备或电路的原型,更重要的是,无需手动进行数学计算。设计人员必须对瞬态分析进行配置,以便收集的数据包含足够多的点。因此,不要局限于将几个频率周期可视化。最好考虑信号的长间隔。在电子设备和电路的设计及使用中,谐波失真是一个需要考虑的重要现象。测量谐波失真对评估信号质量至关重要,它也决定了系统认证的成败。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Guide to Spice Simulation for Circuit Analysis and Design – Part 8: Measuring Harmonic Distortion,由Ricardo Xie编译。)
用于电路分析和设计的SPICE仿真指南-第1部分:简介和网表
用于电路分析和设计的Spice仿真指南-第3部分:时间常数的进一步研究
用于电路分析和设计的Spice仿真指南–第4部分:用于多重仿真的.STEP指令
用于电路分析和设计的Spice仿真指南–第5部分:直流扫描分析
用于电路分析和设计的Spice仿真指南–第6部分:更深入的直流扫描分析
 最前沿的电子设计资讯
最前沿的电子设计资讯