
在前面的文章中,我们准备了适合使用Mathematica进行限幅电路研究的工具。但在这样的计算环境中开始开发热望的例程之前,让我们先对提出的电路进行定性分析。首先,我们将修改上一期文章中提出的限幅电路,添加一个电池,如图1所示。
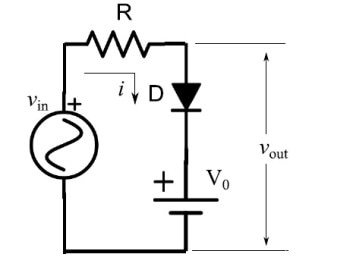
图1:通过添加电池修改限幅电路
为了解决这个电路,我们将考虑图2所示的方案。
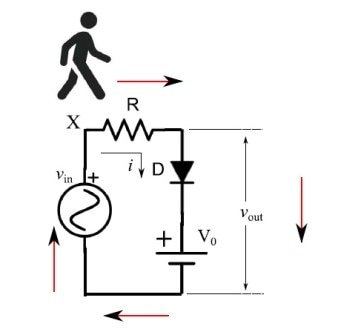
图2:小人按照红色箭头方向运行电路
小人用电压表测量从X点开始的电势。沿着箭头,他会遇到各种电势下降,即:电阻、二极管和电池。与电压发生器(输入信号)相对应,他记录下了电势的增加,然后返回到X点,在那里他显然测量到了相同的初始值。因此,我们可以写出以下等式,其中符号的含义一目了然:
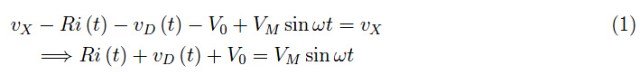
输出信号由下式给出:

理想情况下,二极管的行为就像一个开关:正向偏置时导通,反之则断开(参见图3)。
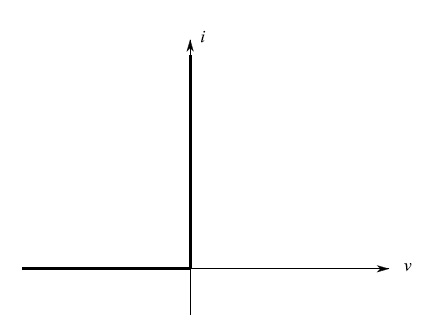
图3:理想二极管的电压-电流特性。二极管正向偏压时短路,反向偏压时开路
在图1的电路中,我们可以设置R=0,因为以下参数在定性上等同于R>0的情况。根据假设,输入信号是一个符号无限变化的函数vin(t)。既不需要周期性,也不需要正弦波形(数学上更简单)。
如果没有电池(V0=0),则在正脉冲波前到达时(vin(t)>0),二极管将处于正向偏置,因此处于导通状态。当负波前到达(vin(t)<0)时,它处于关断状态。插入电池(V0>0)意味着作用在二极管上的有效信号为vin(t)−V0,因此二极管处于关断状态,直到vin(t)−V0<0。最初,这种情况发生在时间间隔[0,t0]内,其中t0是方程vin(t)=V0的第一个根。各个解的参数取决于V0。在不失去一般性的前提下,我们可以假设vin(t)=VMsinωt:

当且仅当以下情况时解才成立:

如果V0<0,则表示我们插入的电池极性错误(即接反);目前,我们不考虑这种情况,即0<V0≤VM。否则,方程(3)无解,电路不传导电流。在周期区间[0,2π/ω]中,我们有以下解:
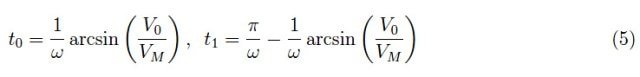
解如图4所示。我们可以得出结论,在周期区间内,二极管仅在t0≤t≤t1时导通。
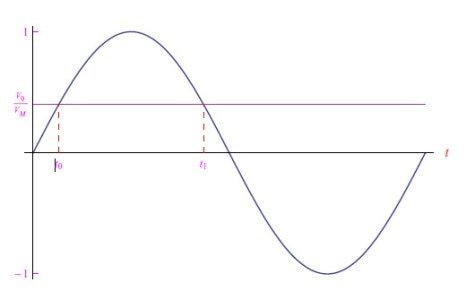
图4:求方程(3)的解
为了表达二极管上的压降,我们使用电压-电流特性。如上一期中所做的那样,对各种量进行无量纲调整,我们得到以下函数方程:

其中:
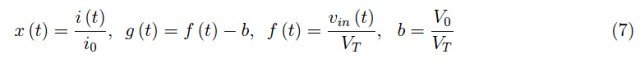
在使用Mathematica解决这个问题之前,最好检查一下方程(6)的第二个因素的第二个指数的参数。在正弦输入的特定情况下,g(t)=(VM/BT)sin(ωt)−b。也就是说,它是在纵坐标轴上偏移量b的正弦振荡,该量等于在VT=26mV上归一化的电池电压。例如,对于电压为V0=0.5V、输入峰值为1V的电池,我们可以得到图5所示的趋势。因此,要获得正确的输出信号趋势(在二极管-电池串联的端子处),必须是0<b<VM/VT。我们通过定性分析得出了这个结果。
总之:无量纲量b可以作为(0,VM/VT)范围内的自由参数。
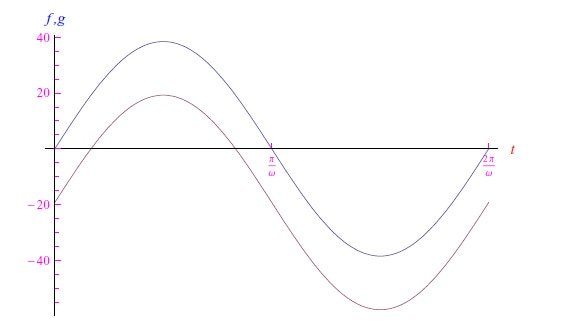
图5:V0=0.1V、VM=1V时无量纲数量f(t)和g(t)的变化趋势
图6中显示了通过使用Mathematica(符号模式)求解方程(6)获得的电流趋势。二极管两端的压降很容易计算,在图7中显示了相应的趋势。
如等式(2)所示,输出信号是二极管-电池串联之间的的电势差。根据之前的数据,我们要求Mathematica追踪其趋势(见图8),从中可以清楚地看到限制效应。
此时,我们可以通过反转电池或二极管的极性来“找些乐子”。第一个操作不会引入物理上有趣的新奇事物。然而,第二种操作却具有数学对称性。事实上,很容易验证,在数学上,二极管极性的反转相当于等式(6)的指数参数符号的反转。例如,使用之前相同的值,我们可以得到如图9所示的输出信号。
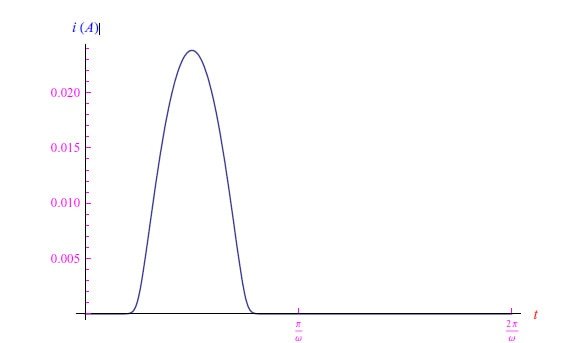
图6:R=10Ω、VM=1V、V0=0.5V、ω=20rad/s时的电流趋势。观察前面定性分析所预见的t0和t1时刻存在的情况
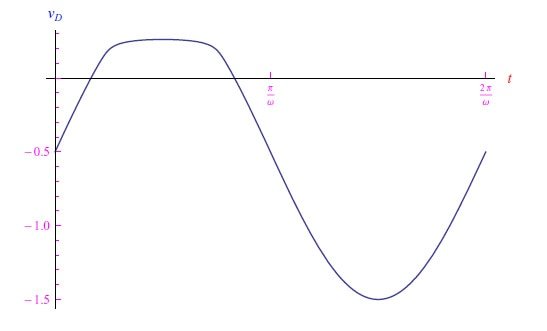
图7:R=10Ω、VM=1V、V0=0.5V、ω=20rad/s时vD的变化趋势
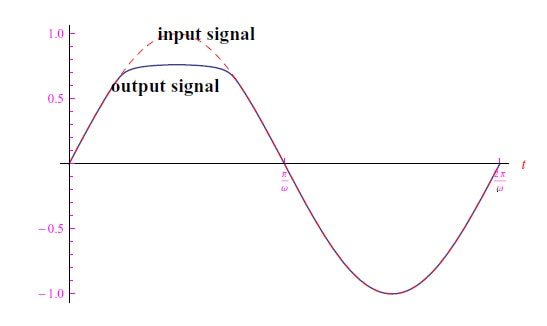
图8:R=10Ω、VM=1V、V0=0.5V、ω=20rad/s时的输出信号变化趋势。
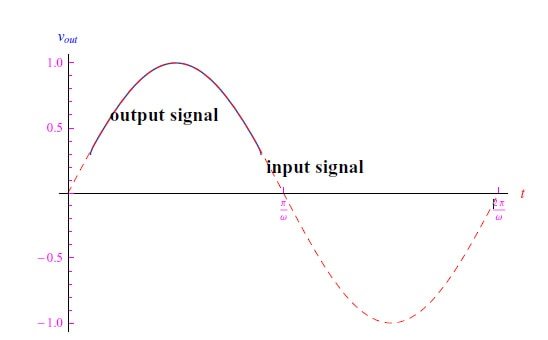
图9:在R=10Ω、VM=1V、V0=0.5V、ω=20rad/s条件下,极性相反的二极管输出信号的变化趋势
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: One-Level Limiting circuit,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯