
我们先来看看图1所示的电路,其中的两个二极管完全相同。
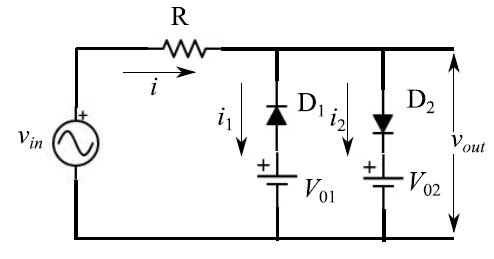
图1:双电平限幅电路(限幅器)
我们采用峰值为VM、角频率为ω的常见正弦输入:vin(t)=VMsinωt。如果我们断开D2和V02的支路,我们就会得到一电平限幅电路,其中二极管极性相反(输出是正弦曲线的波峰)。如果我们现在连接上第二支路,只要满足条件V02>V01,正向偏置的二极管D2就充当限幅器。假设这两个二极管是理想的(在正向偏置下表现为短路,反之则开路),我们就得到如图2所示的输出信号。
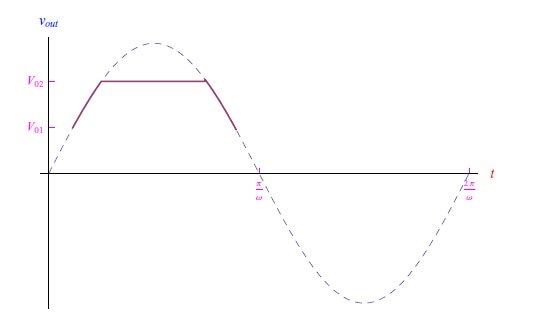
图2:理想条件下双电平限幅电路的输出信号
在更现实的条件下,即考虑二极管的实际电压-电流特性,电路的数学分析是相当复杂的。看图1,根据基尔霍夫第一定律,我们有:

根据基尔霍夫第二定律:

刚刚写出的方程并不足以解决问题。现在让我们分析一下包含两个二极管的网格。为此,让我们这个配备了电压表的小人走过图3所示的路径,从而得到:
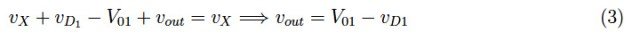
同样,按照图4所示的路径,我们有:
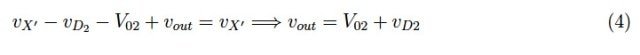
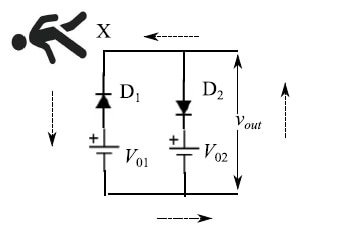
图3:小人沿着虚线箭头所示的路径测量电势
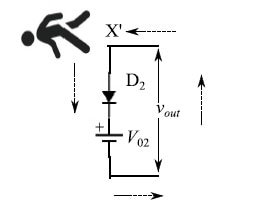
图4:小人沿着虚线箭头所示的路径测量电势
由于二极管是相同的,我们可以对i0项上的各个电流进行归一化,即x1=i1/i0、x2=i2/i0:
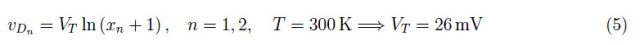
将式(3)和(4)中的vout消去,经过简单的步骤,我们得到:

确定了:
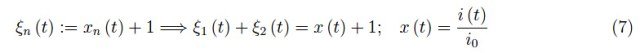
也就是说,ξn是两个支路中的单个(无量纲)电流增加一个单位。
下面是函数方程组:

值得注意的是,根据第一个方程,电流的乘积是一个常数C,并且对于所做的假设(V02>V01)0<C<1。这个结果是预料之中的,因为如果一个支路中的电流增加,那么另一支路中的电流就会减少,因为这两个支路是并联的。进行一些代入后,我们在未知函数ξn (t)中得到如下系统:
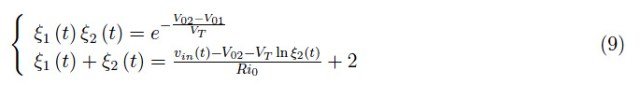
方程(8)第二项右侧对数的存在破坏了计算求解系统的可能性。事实上,Solve指令会警告输出无法进行代数求解,建议使用FindRoot(该指令在未知数不是函数的系统中非常有用)。然而,Mathematica有一个比Solve更强大的语句,那就是Reduce指令,在这种情况下,它会以指数级的加速求解算法的执行时间。
假设电流值较低,我们仍然可以使用在线性项处截断的对数级数:
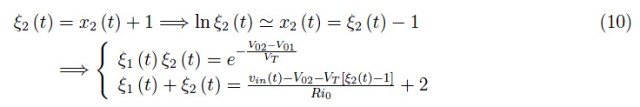
按照这个近似顺序,Mathematica求解函数方程组,之后我们就可以使用方程(3)和(4)之一来计算输出信号。数值数据如下:
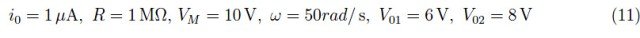
从图5中我们可以看出,所使用的近似值“极其粗略”,因为它只能部分再现正确的趋势。
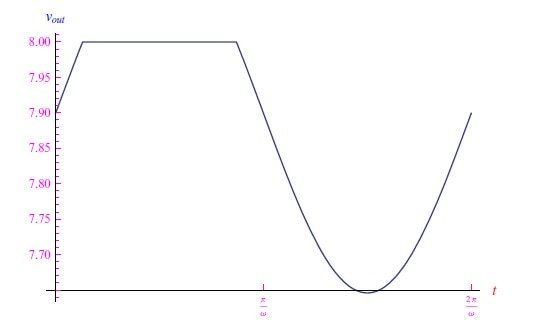
图5:输出信号的趋势,采用在线性项处截断的对数级数的近似值
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Two-Level Limiting circuit,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯