
在上一篇文章中,我们介绍了离散傅立叶变换,最终完成了对采样信号的频率分析。这种有效的工具可用于所有不一定构成物理意义上的信号的数据集。例如,可以通过DFT研究昆虫种群的增长或流行病传染过程中受感染个体数量的变化趋势,以确定是否存在着某种周期性。
在上一篇文章中,我们考虑了一个简单的情况:调幅正弦信号。在进行采样/截断后,很容易就能确定傅里叶频谱中是否存在单个频率:正弦振荡的频率。而对于更复杂的过程,预计会出现更多的频率。问题是:“从存在无限频率的意义上来说,是否存在傅里叶频谱无限密集的信号/过程?”
乍一看,这似乎是一个没有道理的案例,但事实上,这些过程非常普遍,如我们正在谈论的噪音。例如,图1显示了白噪声的典型傅里叶频谱(方差为1,平均值为零)。与往常一样,重要频谱从采样指数的0延伸到1,000(不要与频率值混淆):频谱的第二部分是第一部分的翻版。
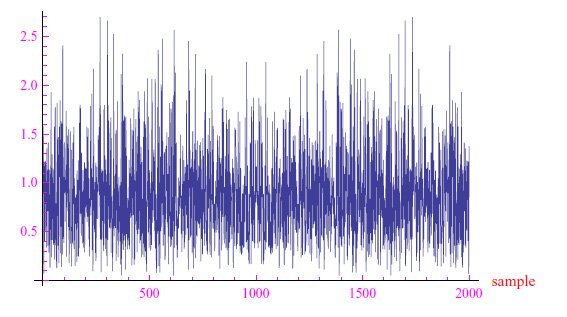
图1:白噪声的傅里叶频谱
白噪声很奇特,因为假定作为时间函数的x(t)值是100%不相关的,那么频谱中存在无限频率。从数学上讲,白噪声是一个在每个点都具有有限不连续性的函数,因此它具有不可预测性。而另一种解决方案是将x(t)表示为一个非唯一定义的函数,即对于给定时刻t,数量x可以有多个值。
在这一点上,描述随机过程的制胜法宝显然是使用统计方法。通过考虑所谓的稳态过程可以实现显著的简化:找到给定x值的概率不依赖于时间。下一步,我们要考虑的不是单一的过程,而是考虑正在检查的进程的大量(最多无限)思维副本。如果我们知道概率的解析表达式,我们就可以对x进行统计平均,通常用⟨x⟩表示。种计算方法避免了确定x的时间平均值这一令人尴尬的问题。事实上,根据平均值的定义:

而这种计算不切实际,原因有二:
正是这最后一种情况为我们提供了解决方案:在无限的时间内,该过程会经历所有可能的配置或我们统计样本的所有思维副本。换句话说,我们可以得出这样的结论:统计平均值⟨x⟩与时间平均值一致(等式1)。这种性质被称为遍历性:因此,一个遍历过程会表现出这一有趣的特性。从数学上来说,确定给定过程的遍历性是非常困难的。但大多数有物理意义的随机过程都具有遍历性。
在图1中,我们得到了均值为零的白噪声的傅立叶频谱。为了数学上的方便,我们总是将自己带入这个条件,即如果⟨x⟩不为零,我们仍然可以从各种表达式中减去该值来重现出先前的情况。由此可见,根据方差的定义有:σ2=⟨x2⟩。但这只不过是总信号强度。现在让我们考虑以下具有幂次级的量ψ(τ)=⟨x(0)x(τ)⟩,τ扮演时间变量的角色。很明显,ψ(0)是方差,而在不同时间,它告诉我们x(0)和x(τ)各个值是如何“相关”的。对于白噪声,我们有:

为了表示这样的对象,狄拉克δ函数可以帮助我们:ψ(τ)=σ2δ(t),即使它不能再现需要积分的ψ(0)。众所周知,狄拉克δ的傅里叶变换是一个常数函数,因此(2)的傅里叶变换是“平坦的”,这正是白噪声功率谱的预期,因为每个频率对信号功率的贡献权重相同。
这些结论有一个共同特征:它们对于任何遍历过程x(t)都是有效的。被称为自相关函数的对象ψ(τ)与x(t)的功率谱之间的联系构成了著名的维纳-辛钦定理的表述:x(t)的自相关函数的傅里叶变换就是x(t)的功率谱。
Mathematica提供了可以仿真白噪声,然后确定其功率谱和自相关函数。对于这种环境,每条指令都被视为一个“函数”,其参数是模式(pattern),因此它们也可以是列表(list)。因此,我们定义了一个PowerSpectrum[x List]函数,其中下划线向Mathematica内核传达x可以是任何东西,只要它是一个“列表”。简而言之,x是一个时间序列(采样和截断的信号)。然后,代码块内的指令将执行傅里叶变换与变换本身的复共轭乘积(根据功率谱的定义)。
根据维纳-辛钦定理,自相关函数是功率谱的逆变换。所以我们定义了一个函数Correlate[x List]。例如,在白噪声的情况下,我们可以得到图2中的趋势,从中我们可以看到在非零时不存在相关性。
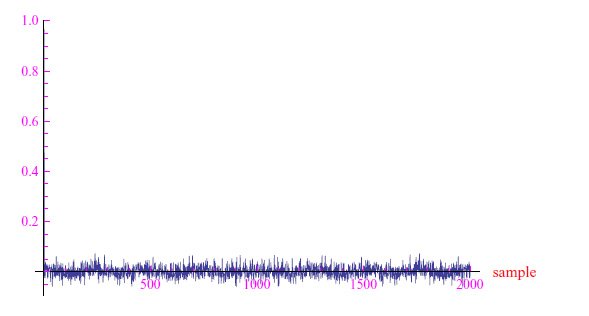
图2:均值为零、方差为1的白噪声的自相关函数
作为该Mathematica脚本的一个应用示例,我们研究一下质数的分布。准确地说,用pn表示第n个质数,我们定义序列:

这相当于连续情况下的导数。通过绘制n≫1时的{δn}图形,我们获得了类似白噪声的趋势。正如我们从图3和图4中看到的那样,Giovanni Di Maria在Octave中证实了这一点。
因此,质数的分布是白噪声或维纳过程的积分。
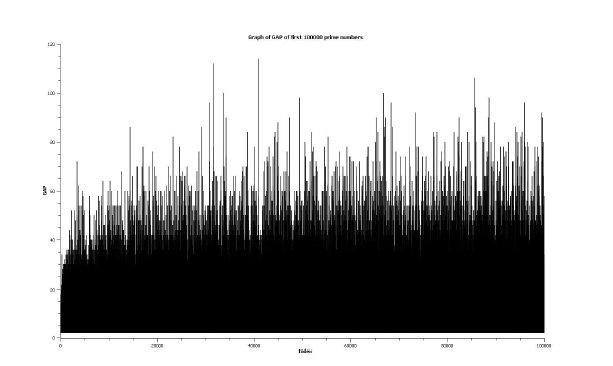
图3:n=1,..2000时{δn}的变化趋势(来源:Giovanni Di Maria)

图4:{δn}的自相关函数(来源:Giovanni Di Maria)
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Noise and DFT/FFT,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯