
信号采样——作为模拟/数字接口的狄拉克梳
假设模拟信号x(t)的傅里叶变换X(f)是已知的,混叠现象就是对模拟信号x(t)进行所谓采样后的结果。
我们所说的“采样”是指:以恒定的时间间隔Tc(采样时间)测量信号,获得xn=nTc,其中整数n在适当的范围内变化(理想情况下为无穷大)。Tc=0.5s时的信号x(t)和相应的采样分别如图1和图2所示。
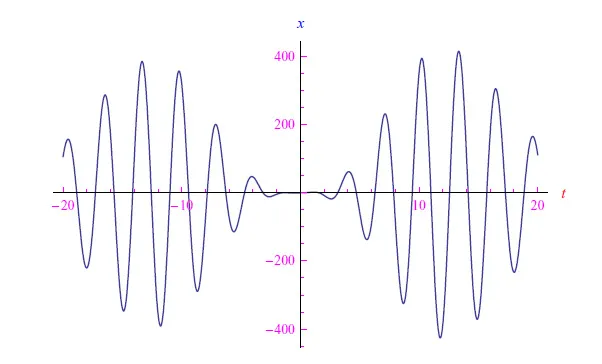
图1:振荡和指数衰减信号的典型行为
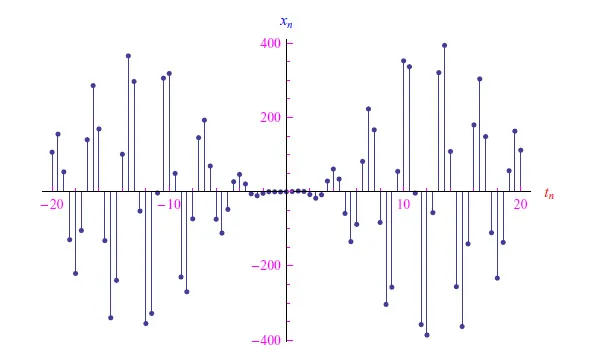
图2:上图中的信号是在Tc=0.5s时的采样情况
在中,我们确定了一类信号的存在性,其傅里叶变换不作为函数存在,而是作为分布存在。对于那个术语,我们指的是定义不当的函数,例如狄拉克δ。准确地说,在符号含义明显的情况下,单位脉冲的计算公式为:

单位脉冲的傅里叶变换是常数函数U(f)=u0。方程(1)在量纲上是正确的,因为δ函数的量纲是其参数的倒数。如果单位脉冲以t0为中心,则有u(t)=u0δ,由此计算傅里叶积分,有U(f)=u0e−j2πft0。然而,物理上有趣的量是频谱|U(f)|=u0e−j2πft0=u0,因为虚指数有单位模。
在明确这一点后,我们首先可以将一系列单位脉冲(或戏称的狄拉克梳)与要采样的信号相关联:

采样信号现在可以写成如下:
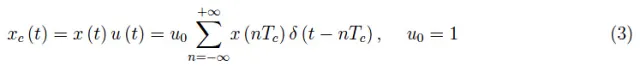
在这里,我们按部就班的引入了用于解决量纲问题的常数项u0=1,然后从这里开始,我们将省略常数项。
因此,我们可以看到狄拉克δ函数的形式允许我们以模拟地方式处理数字信号。狄拉克δ函数,或者更广义地说狄拉克梳,是一种有用的模拟/数字接口。
在确定采样信号(3)的傅里叶变换之前,我们观察到(2)给出的傅里叶变换如下:

可以证明:
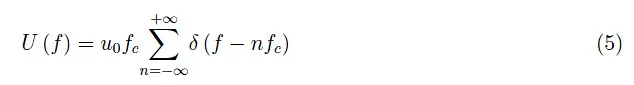
其中fc=1/Tc是采样频率。换句话说,狄拉克梳(2)的傅里叶变换仍然是狄拉克梳,其中各个δ函数的间隔为fc(与u(t)的单位脉冲间隔Tc不同)。这个数学上很优美但物理上令人费解的结果如图3所示。实际上,它可以用简单的物理方法来解释。如果我们在给定阶数时截断数列(2):
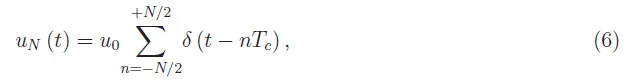
傅里叶变换变为:
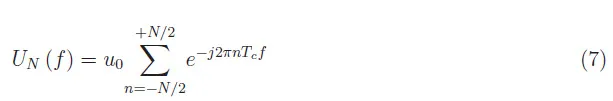
因此,它是N个虚指数的叠加,就像N个正弦振荡的干涉一样。在图4和图5中,显示了N=10和N=20情况下各个模块的图形。从图中我们可以看到,当N→+∞时,无限正弦振荡的干涉再现了狄拉克梳(5)。
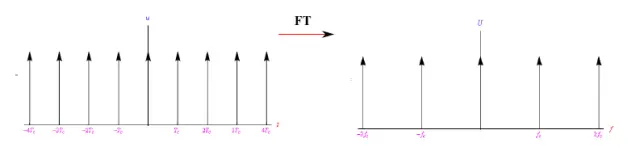
图3:狄拉克梳的傅里叶变换本身就是狄拉克梳,但具有相反的间隔
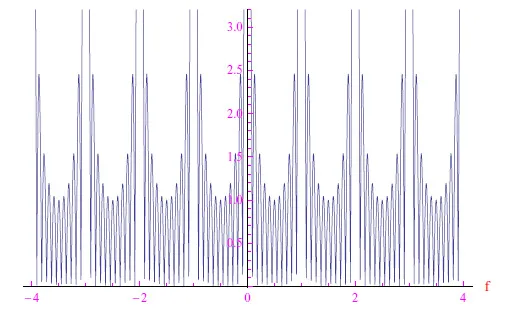
图4:u0=1且N=10时(7)的趋势
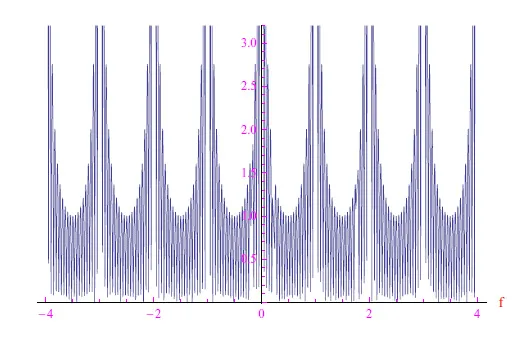
图5:u0=1且N=20时(7)的趋势
此时,我们需要计算采样信号(3)的傅里叶变换:
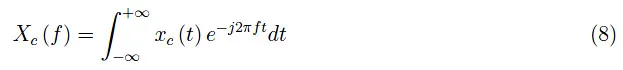
我们假设模拟信号x(t)的傅里叶变换X(f)是已知的。从(3)我们可以看到有两种不同的方法来计算变换:
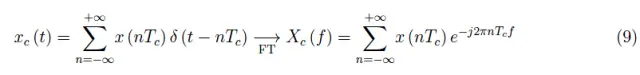
这与(4)类似,不同之处在于现在各个项是根据信号的采样值加权的。由于无法明确数列之和,我们需要考虑第二种方法。根据(3),我们可以写:
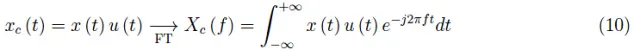
在此,卷积定理可以帮到我们。不过,它是写在频率空间中的,我们首先定义两个信号x(t)、y(t)的变换X(f)、Y(f)的卷积乘积*如下:
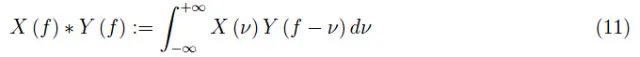
应用上述定理,我们有:

其中FT-1表示傅里叶逆变换。这意味着x(t)y(t)的傅里叶变换是各个变换的卷积乘积:

在卷积积分易于计算的情况下,这一结果非常有用:
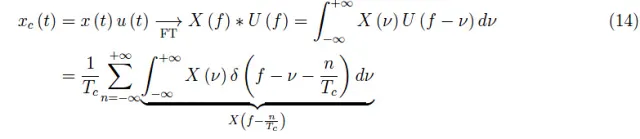
用采样频率来表示,我们最终得到:
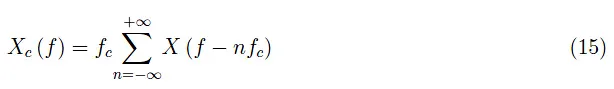
也就是说,采样信号的傅里叶变换只不过是无限次复制的模拟信号的傅里叶变换。这会导致频谱图|Xc(f)|在频率轴的两个方向上无限位移,其中单次位移的振幅由fc给出。
请注意,(15)概括了(5),因为这是采样模拟信号等于1的傅里叶变换。事实上,x(t)=1的傅里叶变换是狄拉克δ函数δ(f)。因此,根据式(15),相应采样信号的傅里叶频谱由δ(f)的无限位移组成。
如图6所示,表示模拟信号的函数x(t)是具有频带限制的:傅里叶频谱在指定频带B=[−fmax,fmax]上达到极大峰值。使用Tc对信号进行采样,使得fc>2fmax,则幅度频谱的位移大于2fmax(图7)。反之亦然,如果fc<2fmax,则会产生频谱重叠,如图8所示,从而产生混叠现象。准确地说,混叠现象阻碍了从变换Xc(f)(通过傅里叶逆变换)开始的采样信号的正确重建。
因此,只有当采样间隔足够短以使信号频带的最大频率fmax>fc/2时,我们才能在没有混叠的情况下工作。该限制值被称为奈奎斯特频率。
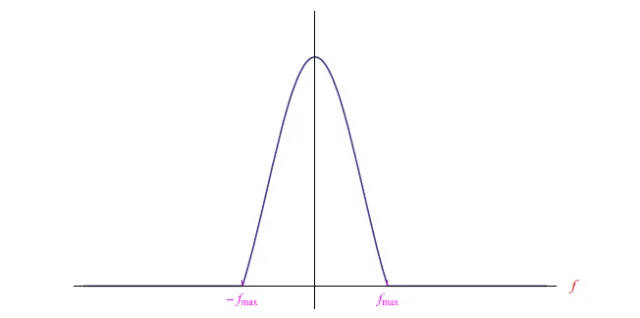
图6:具有频带限制的信号的典型傅里叶频谱
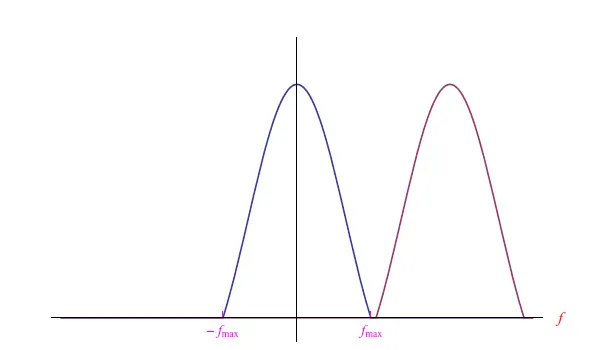
图7:用Tc对信号进行采样所确定的傅里叶频谱的偏移,使得fc>2fmax
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:The Nyquist frequency and aliasing phenomenon,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯