
这篇文章中,我们将开始探索如何伪造一个精确的三角波,并用它来帮助设定伪正弦波的黄金标准。那么,我们的成果如何呢?
不久前,我需要(或者说想要)一台袖珍音频正弦波发生器:简单、稳定、可重复、单组控制电位器、9V电池供电。把三角波压扁成正弦波,这个方法看起来很合适。虽然原理很简单——制作一个三角波,通过一个电阻馈入一对背靠背二极管,从二极管中获取正弦波并将其放大——但驱动电平和电阻值都被证明是至关重要的。它的效果很好,让我想知道它的极限在哪里:我们到底能在多大程度上接近这样的正弦波?
这篇设计实例(我将保持其实用性并尽可能避免数学计算)采用了我最初的概念,并对其进行了进一步改进,或许可以与另两篇关于振荡器的设计实例——《双RRIO运算放大器可产生缓冲、可调的三角波和方波》和《矩形波和三角波函数发生器》——相辅相成。我们将分阶段进行,从生成三角形开始,继续进行压制,然后尽可能消除其他误差源。
起初,我打算通过计算线性递增馈电时电阻馈电二极管上的电压来建模,然后将其与单象限上的相应正弦值进行比较,查看两者之间的差异,不断迭代,直到出现馈电电压和电阻的最佳值。然而,维基百科上的词条“Diode modelling”(二极管建模)让我失望了,尽管它很有启发性;它还解释了SPICE使用的变通方法。我需要一种现实生活中的方法,无论如何,这种方法往往更有趣。
我最初的出发点是图1所示的著名的振荡器,它有效地结合了积分器和施密特触发器。RT和CT分别是调谐电阻器(可变)和电容器(可能是开关状态)。
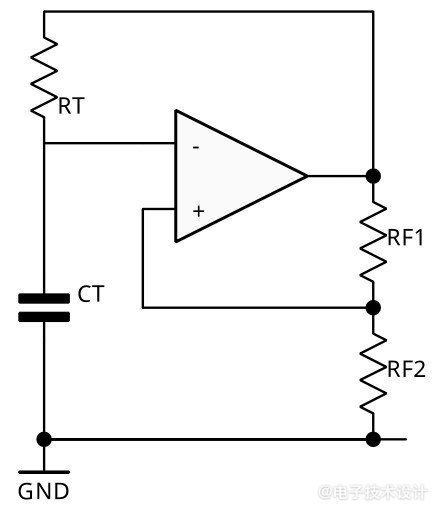
图1:一种有效结合了积分器与施密特触发器的基本振荡器。
当运算放大器的输出为高电平时,CT通过RT充电,直到其电压达到由RF1与RF2之比给出的跳变点,然后将输出驱动为低电平,从而使CT反向充电,直到达到相反的跳变点,如此无限重复。因此,输出为方波,CT上出现指数三角波。虽然占空比正好为50%,工作频率在电源变化时也很稳定——假设电源轨平衡,运算放大器输出轨到轨——但无论是方波还是指数波,对于产生正弦波都没有什么用处,尤其是当它们的振幅取决于电源时。(我最初的设计规格是PP3/6LR61电池,新电池时电压约为9V或±4.5V,旧电池的电压则低很多。)
我们需要一种不同的方法,图2显示了新电路的核心。(假设正负电源轨平衡。)我曾想过,三角波的最佳电平是否恰好是每个方向一个二极管压降,我们是否可以根据二极管的正向电压(VF)来定义一切:这就是这个想法的萌芽,也是现在这篇设计实例的萌芽。
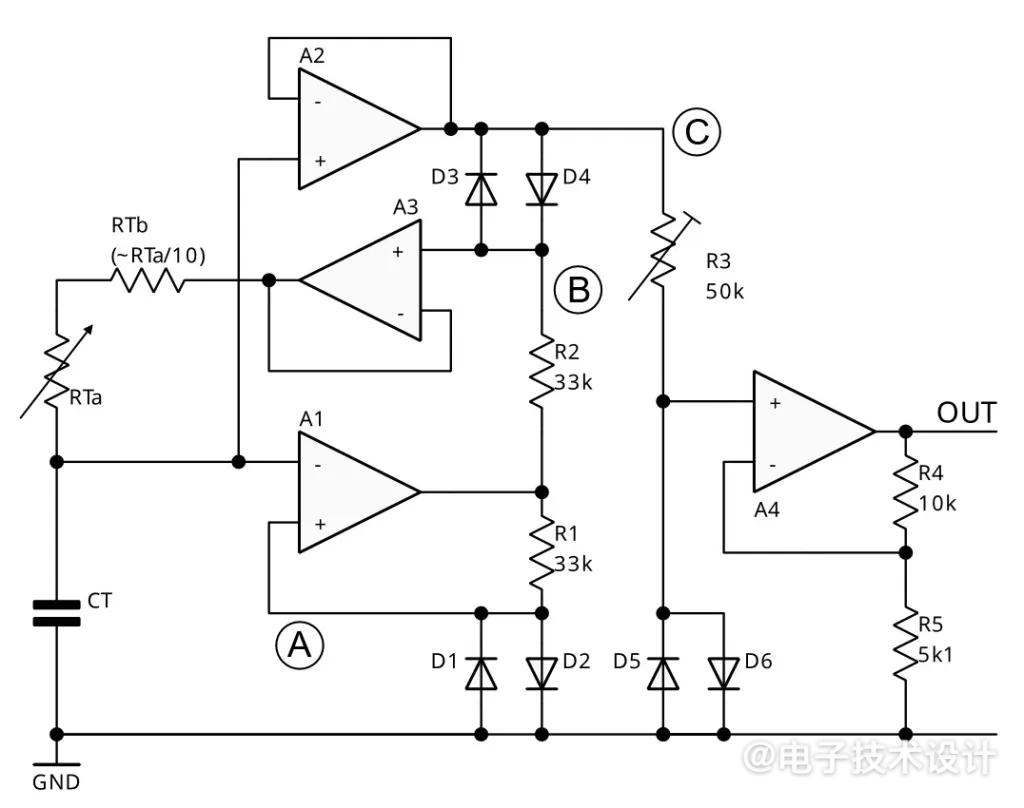
图2:简单、新颖的三角波发生器和正弦转换器。
将三角波的生成与正弦波的转换有效地结合在一起,可以消除一阶误差,从而最大限度地减少频率随电源电压和温度的变化,并可根据频率将总谐波失真(THD)最终微调至0.7%至3%之间。还有其他方法可以通过排列相同的元件获得相同的结果,但这种方法可以最大限度地减少延迟,因此效果更好。稍后我们将进一步改进。
首先,我们用一对二极管D1和D2代替RF2,这样跳变点就由它们的VF定义了,CT上的电压现在在±VF的范围内摆动。接下来,我们添加自举功能,使波形线性化。(设计实例“”(使用一个运算放大器的线性斜坡发生器)展示了该技术的另一个应用。)RT由CT电压的缓冲副本加上/减去D3/D4上的电压驱动,因此其两端的电压始终为2VF,从而产生线性斜坡。因此,CT的电压以及A2的输出是一个峰峰值振幅为2VF的纯三角波。电源变化在很大程度上被R1和R2所吸收——并非完全吸收,但我们可以将其视为二阶效应而忽略不计;振荡频率在跨轨3至15V范围内均在1%以内。A3对RT的馈电进行缓冲,使R2和D3/D4保持空载。图3显示了电路的波形以及R3在约1kHz时进行严格调整后的输出的快速傅里叶变换(FFT)。
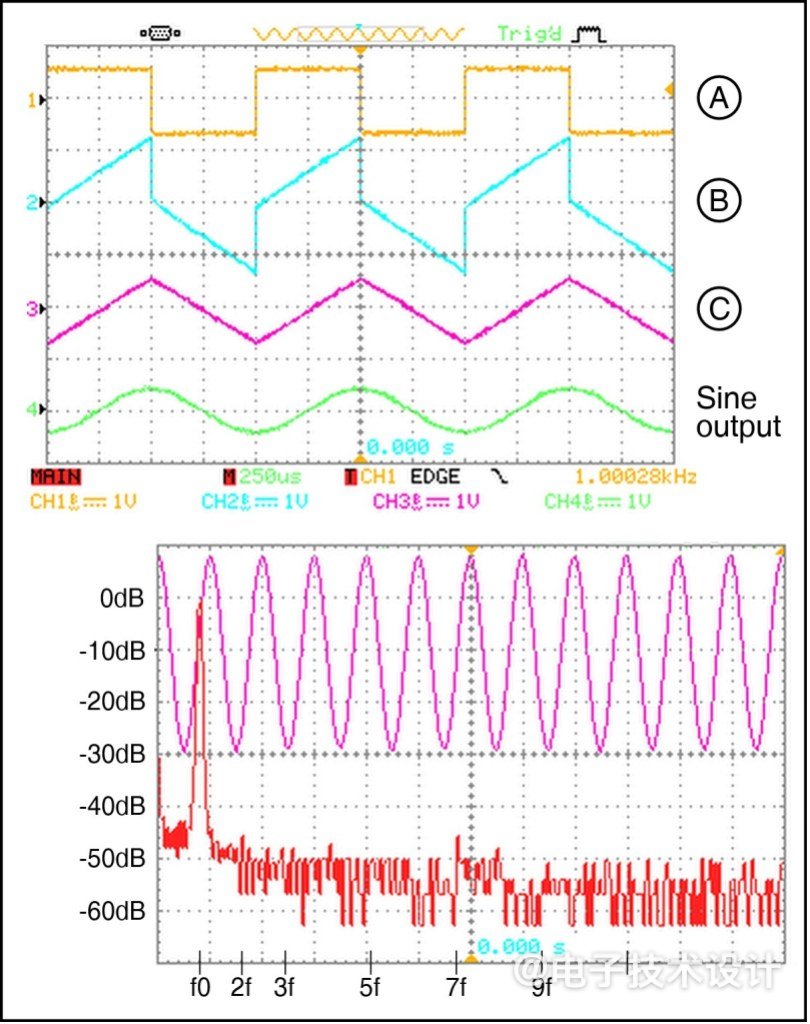
图3:图2电路的波形和FFT图(上),以及R3 在约1kHz时进行严格调整后的输出FFT(下)。
二极管本身对温度敏感,其正向电压每摄氏度下降约2mV。因此,跳变点会随之变化,从而可能导致工作频率随温度升高而增加。然而,D3/D4两端的电压会以相同的幅度下降,从而按比例减少对RT的驱动,进而抵消温度变化引起的变化。现在,我们得到了一个出色的对称三角波,其振幅为2VF pk-pk,频率稳定,不受温度和电源电压变化的影响。
由于二极管的电流和电压之间的对数关系,通过R3将其馈入D5/D6,可将其压制成合理的正弦波(但请再次参阅维基百科上的“Diode modelling”词条)。D5/D6的VF随温度下降,但三角形的振幅也随之下降。A4放大正弦波,输出电平约为2.2V pk-pk——0.775V RMS,即0dBu。(图中未显示CT的范围切换、输出电平控制电位器和3倍增益输出放大器。)使用示波器的FFT对R3进行微调,以实现最小的三次谐波含量;20kΩ左右是最佳的折衷值。
然而,当设置为1kHz时,其他频率下的失真会严重得多,尤其是8kHz以上的频率。这是由于A1的性能造成的,我们稍后再讨论这个问题。虽然我们关注的是三次谐波,那么其他谐波呢?一个简单的带反馈的双T形陷波滤波器,频率接近1kHz、q值为2、增益为10,可以使示波器相当基本的FFT显示出之前隐藏在采样噪声中的谐波。这清楚地显示了三次谐波,但也揭示了当R3变化时,五次谐波的电平也发生了变化,但与三次谐波的变化不同步,这表明平衡主要取决于R3上的电平以及R3的值。七次及以上的高次谐波基本保持不变。
是时候搭建一个测试平台来检查到底发生了什么,但首先让我们来看看振荡器的问题。
振荡器的频率理论上由1/4RTCT给出——想想CV=IT,其中C是电容,V是电压(变化),I是充电电流,T是充电时间(都是线性斜坡)——但是频率越高,与现实的不匹配和传播延迟就越严重。这主要是A1造成的,因为它必须加到RTCT中。对于1kHz的频率,在CT=10nF时,RT的测量值为22.8kΩ,而不是25kΩ;1MΩ+10nF为24.5Hz;10kΩ+10nF为2.12kHz;10kΩ+1nF为15.1kHz。
A1是TLV237x运算放大器(3MHz、16V、RRIO)。它的内部信号延迟和有限的压摆率意味着三角波振幅会随着频率的增加而稳定上升,到25kHz左右会翻倍,从而过度驱动正弦转换,导致失真增加。理想情况下,它应该是一个快速比较器,但那些具有合适电源电压和双极性轨到轨输出的比较器目前似乎标价为两位数(以英镑/美元/欧元为单位),交货时间为三位数(以周为单位)。(合适的5V器件和匹配的运算放大器可从多家制造商处购买。)为了治标不治本,我们必须在产生振幅后使之稳定。
我研究了几种类型的AGC(自动增益控制,严格来说是自动电平控制)电路。JFET是通常的起点,但其本身是非线性的,需要很多东西来限制其两端的信号电压,并抵消其剩余失真——几个运算放大器和几个微调器才能做到这一点。光敏电阻(LDR)可以避免线性问题,虽然这种解决方案可能看起来简单粗暴,但在这里却非常有效。图4显示了经过修改的新电路。
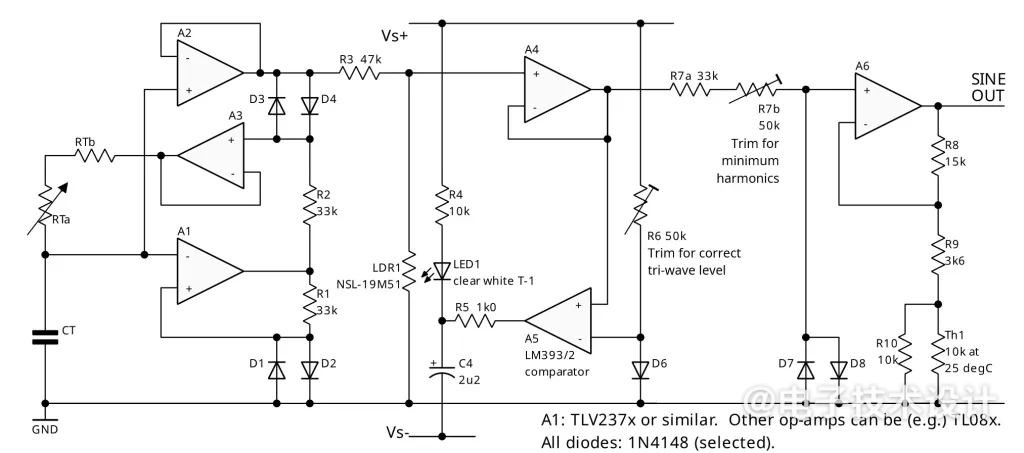
图4:带有AGC的新型三角波发生器和正弦转换器测试电路。
A5是LM393双比较器的一半,当三角波尖端超过参考值时,它就会感应到,然后驱动LED1点亮LDR1,LDR1的电阻下降,从而减小R3上的信号。参考值由R6和D6提供,它们将跟踪振荡器本身的R1和D2。A4对输出进行缓冲,现在输出在10kHz以下几乎恒定,在25kHz时仅上升10%。(LDR1是Silonex NSL-19M51,LED是普通的T-1透明白色8cd器件,不过高效的550nm绿色/青色器件可以更好地匹配LDR的响应。厚厚的黑色热缩管将它们连接并屏蔽起来。)用一个串联下拉二极管代替R5的运算放大器也可以工作,但由于其响应速度较慢,只能达到10kHz左右。
在很低的频率下,过冲很小,因此使用图2中的振荡器时,LED几乎不会扰动LDR。当来自该振荡器或其他信号源的输入超过10V pk-pk时,三角波电平仍由VF确定:AGC只会更努力地工作。不过,最好先将高电平调低。
现在,我们有两种伪造正弦波的方法:一种是从振荡器本身定义的电平开始,另一种是任意设定电平。
不管是哪种信号源,我们现在都有了一个振幅由D6的VF定义的三角波,但这真的是最佳电平吗?
从直观上看,这似乎与压制二极管的VF相同,前提是串联电阻是理想的。通过微调R6和R7,三次和五次谐波完全消失了!如图5所示。
但是,只要任何地方稍有不匹配,谐波之一或两者就会回来。三角波电平需要精确到毫伏级,而A5的输入偏移意味着R6必须可调。当R6被一个向D6提供约275µA电流的精密电流源(图中未显示)取代时,效果最好也最稳定,因为它消除了二阶电源效应。(由于偏移,电流比预期的要大。)R7的临界值非常接近R1/R2(接近33kΩ),因此,如果元件完美且无需AGC,R1、R2、R6和R7将完全相同,临界值接近30kΩ。这个问题就留给理论家们去研究吧!
使用陷波滤波器去除基波后发现,七次及更高次的谐波现在占主导地位,无法调谐掉。(请忽略那些讨厌的残留的偶次谐波。)七次谐波约为-50dB,即0.3%;之后,谐波次数越高,分贝值越低。图5是一个综合轨迹:顶部是原始三角波和产生的正弦波,以及失真产物(谐波),是其比例的100倍;下方是其FFT。这意味着失真极限总共约为0.4-0.5%。
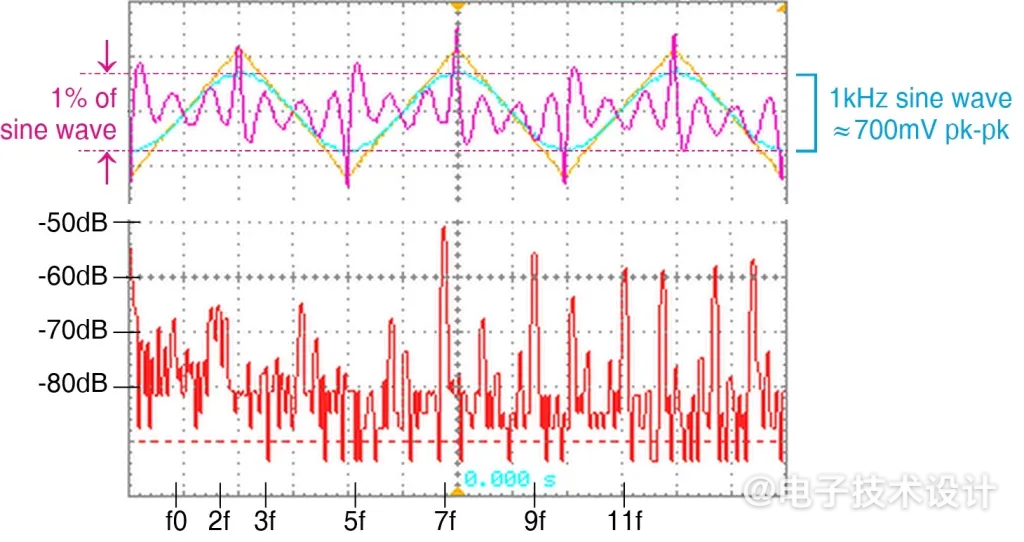
图5:图4电路的结果。上面的轨迹显示了原始三角波和由此产生的正弦波,谐波的比例为100倍。下面的轨迹是滤除基波后的谐波单独的FFT。
二极管的输出电平呢?凭直觉(以及波形的几何形状),正弦波的振幅应该是三角波振幅的1/√2,但现在它错了:所有测量结果都集中在0.666……虽然数字看起来不对,但残余谐波可能是造成差异的原因。我希望熟悉各种正弦序列定义及其与傅里叶分析的关系的数学家会发现答案是显而易见的。
A6对新产生的正弦波进行缓冲并放大。请注意,我们在增益定义网络中添加了Th1——一个标准10kΩ(25℃)热敏电阻。虽然振幅随温度的变化在实际使用中并不重要,但对其进行补偿似乎才是正确的。根据LTspice提供的信息,该网络将提供我们所需的增益,在0至50℃范围内将正弦波振幅提升至2.2V pk-pk,即0dBu。(这就是这里使用的唯一一点模拟。我希望他们的二极管模型是好的。)失真仍随温度变化。虽然D6和D7/D8在隔离状态下是匹配的,但它们的驱动电流不同,因此它们的功能VF既不匹配,也不完全随温度变化。也许将另一个NTC热敏电阻与R7混合能解决这个问题……
需要注意尽量减少二次谐波失真或波形不对称。尽管除AGC外,电路是对称的,本质上也是平衡的,但电源轨必须匹配良好,否则会产生二阶效应。二极管必须成对仔细匹配正向电压。(在本项目和其他项目中,将约50个1N4148贴在一张纸上,对每个二极管进行测量和注释,然后选择成对的二极管,效果很好。)令人惊讶的是,双二极管,或我已检查过的双二极管,内部的匹配度并不高。运算放大器内的偏移会导致轻微的不对称。我通过在电源上连接一个100kΩ电位器,并从其滑块到R3和LDR1的结点连接一个10MΩ电阻器(图中未显示),从而消除了大部分不对称现象:虽然对电源变化有点敏感,但还是很有效。
谐波含量仍会随频率上升,尽管比以前少得多,但在现实世界中,如果3次和5次谐波明显低于7次谐波,我们就做得很好。超过3kHz时,失真开始上升,但谐波逐渐被推至20kHz音频频带的理论上限之外。我估计,在约8kHz时,THD会达到约1%(-40dB),而在20kHz时,THD会达到约3%(-30dB)。该电路的工作频率可远远超过100kHz,但不能推荐波形纯净度!(到25kHz左右,三角波已经变成了相当不错的正弦波。)
由于A1的性能,在低频下校准的调谐刻度在较高频率下将无法匹配:固有延迟会影响调谐规律以及三角波的振幅。在我最初的制作过程中,我使用量程选择开关的备用部分来改变RTb(额外的末端电阻),这有助于将刻度的两端保持在5%以内。
我们的探索已经接近尾声,在探索的过程中我们发现了一些有趣而有用的东西。我们有一种新颖的振荡器,这种振荡器本身就是产生压制正弦波的理想选择,而且我们还能精确地将其他信号源与该过程相匹配。我们对可能的极限有了更好的理解,但也找到了一些优化实际效果的好方法。此外,还有许多未解之谜,需要对底层数学进行深入思考!
我们的经验总结是:为了获得最佳性能,所运用的三角波必须具有与压制二极管的VF完全匹配的振幅(如果它们的驱动方式与该三角波参考方式相同的话)。
但是,把三角波压扁永远不可能得到纯正弦波,因为即使我们驯服了最低次谐波,高次谐波的尖锐牙齿仍会向我们咬来。当我们解决了所有其他问题后,我们还不如把所有这些器件都用在“合适的”正弦波发生器中,使用双积分器/双二阶环路振荡器,甚至是文氏电桥,这样失真更低,性能也更纯净。
—Nick Cornford在10岁时制造了他的第一台矿石收音机,此后他设计了专业音频设备、许多数据通信产品和技术安全套件。后来他终于退休了,基本上算是吧。
(原文刊登于EDN美国版,参考链接:Squashed triangles: sines, but with teeth?,由Franklin Zhao编译。)
本文为《电子技术设计》2024年3月刊杂志文章,版权所有,禁止转载。免费杂志订阅申请点击这里。
 最前沿的电子设计资讯
最前沿的电子设计资讯