
在研究晶体管的输入特性时,我们注意到pn结中已经存在VT项。在本文中,我们将从微观的角度描述这个量,同时也从能量的角度进行解释。
众所周知,pn结的电路行为是通过指数型的电压-电流特性进行描述的,其中归一化/量纲化项出现在指数参数中(除非有一个系数η,它可以调节耗尽层中的复合效应/生成)。我们讨论的是温度的电压当量,这在结二极管的研究中已经介绍过:

其中:T为结温;kB是玻尔兹曼常数;q是电子电荷的绝对值。
为了从微观上解释温度的电压当量,我们首先回顾一下电荷的迁移率定义:

其中vd是漂移速度矢量的大小,E是电场矢量的大小。准确地说,如果没有电场作用在结点上(因此结点处于开路状态),则移动电荷就会在热能kBT的作用下进行随机运动。其结果是平均运动为零,即没有特定的运动方向。相反,施加电场(即在结上施加电势差) 会导致电荷以平均速度vd净流动。
话虽如此,表达式(1)还是从统计热力学的角度出发,通过将载流子(电子/空穴)的扩散D与相应的迁移率µ联系起来的关系(爱因斯坦方程)得到的。这种关系是线性的,比例系数为VT:

从能量的角度来看,VT的解析表达式具有简单的物理解释。考虑到我们在耗尽层研究中关于电势和势能之间差异的考虑,我们可以简单地得到:
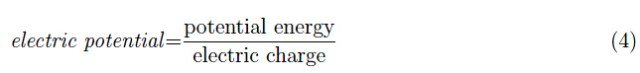
在符号的选择上存在很多混淆。例如,在力学中,势能用V表示,而势用U表示。一个直接的例子是,对于一个放置在高度z处的质量为m的球。地球引力场产生的势能为V(z)=m∙g∙z,而作用在球上的力(重力)的势写作U(z)=g∙z。
表面上看,这是一个微不足道的问题。实际上,它在概念上很重要,因为它告诉我们势能是质量乘以相应势的乘积:V=m∙U。这个结果普遍有效:要从电势转换为电势能,我们必须乘以“电荷”,所以它可以是重力也可以是电力。因此,式(4)可以改写为:

温度的电压当量,即热能,为W=kBT。由此可见,即使VT不是电势,它仍然是一个具有相同量纲的量。从物理上讲,这个量考虑了随机运动的影响,因此在温度为绝对零度时会消失。然而,经典的电压-电流模型无法应用于低温范围,因为当T=0时,半导体会变成绝缘体。
就半导体而言,无论是简单的结型还是晶体管,我们在电路层面测量到的都是在受量子统计力学调节的亚微观背景(电子/空穴)中发生的一系列过程的附带现象。这种附带现象在最显著的位置中赋予了确定性特征,而在背景中没有对应物。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Voltage Equivalent of Temperature and the Einstein Equation,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯