
在前面的文章中,我们忽略了两个结JE(发射极)、JC(集电极)处的耗尽层。在本文中,我们将研究耗尽层对PNP晶体管基区“有效电气长度”的影响。
在单个PN结的情况下,我们详细研究了不同电荷分布的耗尽层。让我们回顾一下其显著的影响。在图1中,我们用A-表示受体原子(带电荷q=-e的负离子,其中e是电子电荷的绝对值);NA是PN结p区中此类原子的浓度。与单个A−对应,我们会发现一个空穴,用h表示。成对的(A−,h)的总电荷为零。对于均匀浓度NA,我们期望在整个p区中(A−,h)的分布同样均匀。
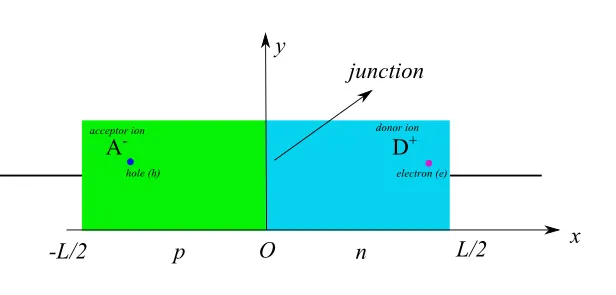
图1:PN结开路。在p区,仅标出了1个受体和1个空穴。这只是为了便于作图,单位体积它们的浓度是NA。n区域也会出现类似的分布
然后我们用D+表示n区中的供体原子(带电荷q=+e的正离子)。如果ND是这些原子的浓度,则对应于单个D+我们能找到一个电子,用e表示。(D+,e)的总电荷显然也为零。对于均匀浓度ND,我们期望(D+,e)在整个n区域中均匀分布。
由此可见,因为没有外加电场(开路),p区和n区的总电荷为零。然而,电中性条件下的电荷分布与上述情况不同。事实上,即使电荷整体为零,我们也可以在局部测量到从p区到n区的电荷梯度(反之亦然)。这就决定了空穴从p到n的移动(电子反之亦然),直到达到没有电荷移动的稳定状态。
此外,在结附近,空穴会与电子重新结合。最终的格局是在晶格的节点上出现大量非中性的A-/D+离子,其浓度可维持电中性状态。因此我们有一个耗尽层DL,由于势能存在双势垒(一个用于空穴,另一个用于电子),稳态结构得以实现。
相应的电势(势能除以单个粒子电荷)就是接触电势V0(也称为内建电势)。原则上,这种势垒是量子可穿透的(隧穿效应),然而,由于单粒子动能较低,隧穿效应的概率可以忽略不计。如果掺杂是对称的(NA=ND),则DL也相对于结对称。在相反的情况下,它在掺杂程度较低的区域中扩展,并且DL的幅度变为:

其中右侧项是相应区域中DL的幅度。最后,我们要记住,结的反向极化意味着DL的扩展,因为在p区空穴倾向于向左移动,这使得其他离子电荷未被覆盖。同样,电子在n区向右移动。这个结论是通过仔细考虑能量得出的:反向极化会增加势垒的高度。此外,通过增加反向偏置的绝对值,DL会进一步扩展,直到出现击穿。
就晶体管而言,有两个DL区,一个对应于JE,另一个对应于JC。按照惯例,我们以PNP晶体管为例。由于该器件的行为本质上是由空穴主导的,因此我们尝试在掺杂中保持强烈的不对称性:与n区(基极)相比,p区(发射极、集电极)呈现出更高浓度的杂质。因此,如果NA是p区中受体的浓度,并且ND是n区中供体的浓度,则我们有NA≫ND。如上所述,在开路条件下,单个DL向基极扩展(图2)。
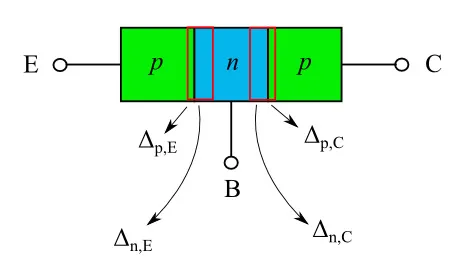
图2:PNP晶体管中的耗尽层。与简单的PN结相比,该图的复杂之处在于JE和JC彼此相对,因此JC上的DL是JE上的DL的镜像
如果DL,E和DL,C分别是JE和JC的耗尽层,则我们用ΔE、ΔC表示单个DL区域的幅度。显然可以得出以下结论:
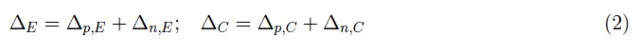
其中Δp,E是发射区中DL,E的幅度。如前所述,我们有:
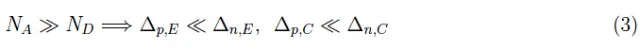
但Δp,E=Δp,C,Δn,E=Δn,C,因为发射极和集电极具有相同的浓度NA。它遵循ΔC=ΔE,因此我们在数学上证明了图2的合理性。
现在,让我们考虑一下处于有源区的同一晶体管。回想一下,在这种结构中,JE结是正向偏置,而JC结是反向偏置。重复前面讨论的能量方面的考量,我们发现JE处的耗尽层由于正向极化导致的势垒降低而减少。当VEB值恰当时(图3),JE中的DL区域的幅度可以忽略不计,而JC上的DL区域与没有极化时相比明显扩大。
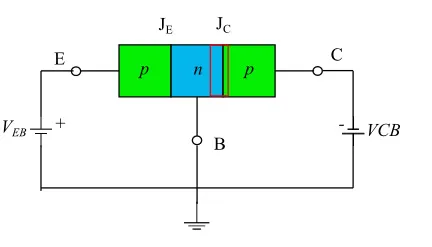
图3:晶体管处于有源区
如果LB是基区的冶金宽度,则有效电气宽度为L′=LB−ΔC。这就是Early效果(基区宽度调制)。
因此,随着|VCB|增大,基区的有效宽度减小。这意味着IpC1的增加,即来自发射极的空穴所产生的电流增大,这些空穴不会与基区的电子发生复合。由于基区中的电子更加稀疏,因此电子与空穴复合过程产生的阻尼不可忽略。现在让我们来回顾一下IpC1=αIE,即发射极电流的一部分,因此0<α<1。由此可见,在|VCB|增加的同时,如果IE相同,α也增加,但仍保持在1以下。
在更现实的描述中,IE也会因基区复合过程的阻尼而增加,这决定了空穴浓度pn(即n区)的增加,并因此决定了发射极电流IE的增加。
最后,我们注意到|VCB|不能无限增加,因为存在一个临界值对于|VCB|crit,L′=0。正如单个PN结的情况一样,它决定了晶体管的击穿。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: The Early Effect,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯