
忽略基极电流的影响,我们将证明PNP晶体管等同于单个pn结,其电压-电流特性在正纵坐标轴上适当移动。这样,我们就可以快速确定该器件的电压放大倍数。
考虑到上一期文章的结果,让我们来看看图1的方案,其中在有源区中看到一个带有负载电阻RL的PNP晶体管。新颖之处在于我们引入了辅助变量x、y、z、ξ,使得数学步骤更加清晰。因此,y是流过发射极-基极结JE的发射极电流。根据符号明显的含义,我们有:
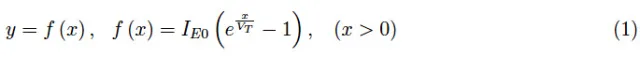
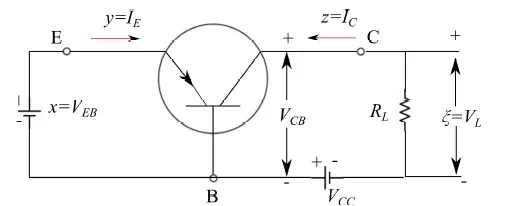
图1:有源区中带有负载电阻的PNP晶体管
正如上一期文章所见:

应该注意的是,在图1中,IC的方向是常规的:由于电荷载流子(空穴)沿相反方向移动,因此方程(2)中IC<0。
在方程(2)中,0<α<1,其中α约等于1(发射极扩散的空穴中不与基极电子复合的部分)。通过适当的掺杂,可以获得α=1。
实变量f的任何实值函数:X→Y都可以解释为接受输入量x并返回输出量y的器件。该过程由图2的定向图表示。
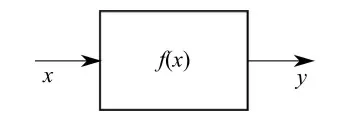
图2:输入x由f(x)处理。结果是y=f(x)
在我们的例子中,y是发射极电流,因此构成了实现集电极-基极结JC的器件的输入,其输出为z=g(y),其中g(y)=−αy+IC0。后者是由电阻负载RL组成的器件的输入,因此ξ=RL|z|=−RLz。就有向图而言,我们可以得到图3中的框图。

图3:PNP晶体管的抽象示意图,通过函数f(x)的非线性可以推断出该器件的非线性行为。然而,其余函数g(y)和h(z)是线性的
众所周知,在数学分析中,这相当于考虑复合函数ξ=h(g(f(x))),即:
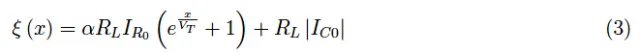
由此可见,ξ(x)/RL是结型二极管的电压-电流特性,沿|IC0|的纵轴正方向平移。因此我们得出以下结论:
忽略基极电流,PNP晶体管相当于单个pn结,其电压-电流特性偏移|IC0|。
图4显示了函数(3)的图形,该函数表示电阻负载RL两端的电压与VEB的函数关系,其中我们考虑静态条件:

其中Vγ是JE的偏置电压。该偏置电压值唯一地确定了JE的工作点(x0,y0),因此确定了笛卡尔平面xξ中的P0(x0,ξ0)。
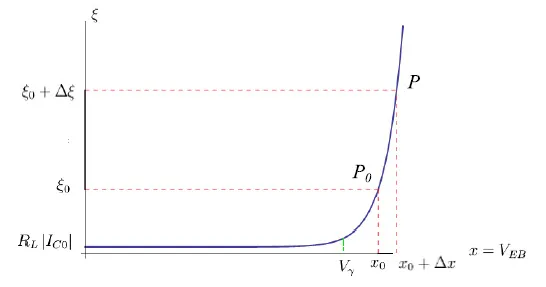
图4:函数(3)的图形
如果我们在x0上叠加一个幅度为Δx≪1(即弱信号)的信号,工作点就会移动到Q,如图4所示。通过暂时恢复物理变量,我们得到了符号的明显含义:Δx=Vin, Δξ=Vout。从图中,我们看到Vout≫Vin,因此发生了电压放大,我们将尝试对其进行量化。这是因为在正向偏置条件下,结几乎是短路的。对于著名的分析定理(微分定理),我们有:

其中,o(Δx)表示比增量Δx更高阶的项,而dξ=ξ′(x)Δx是函数ξ(x)的微分。我们感兴趣的是x0的一阶导数所假设的值。计算完成后,我们得到:

其中r(0)是以x0计算的JE的微分电阻。由于我们考虑的是Δx的微小增量,因此在方程(5)中我们可以忽略高阶项:

它遵循:

其中无量纲量A是电压放大倍数。回想一下,α大约为1,所以A取决于负载电阻与JE微分电阻之间的比值。后者的典型值为40Ω,因此,对于3000Ω的负载,A=+75。
在能量方面,可以按如下步骤进行。我们用Pin表示与输入信号Vin=Δx相关的功率,因此Pin=ΔxΔy。最后一项是集电极电流的增加。类似地,Pout是与输出信号Pout=RL(Δz)2相关的功率。计算完成后:

我们通过观察得出结论,不等式Pout≫Pin并不表示违反能量守恒定律,因为直接计算就能得出结果:

右侧的第二项是对发射极结和集电极结进行偏置的电压发生器提供的功率。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Transistor as an Amplifier,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯