电力电子科学笔记：共发射极结构

在本文中，我们将研究共发射极结构(最常用)，其中晶体管的发射极充当输入/输出接口。Gsoednc

在共发射极结构中，输入/输出回路共享发射极。我们首先看看如何从共基极结构转移到共发射极结构。像往常一样，我们参考PNP晶体管，在不失一般性的情况下，我们假设器件设置在有源区：正向偏置发射极结、反向偏置​​集电极结(图1)。Gsoednc

现在，我们执行以下操作：Gsoednc

• 断开极化。
• 在绘图平面上，旋转+π/2(即逆时针方向)，如图2所示。
• 与前一个相比，执行空间反射以创建一个镜像结构(图3)。
• 再极化：将发射极接地，然后连接负载并打开电源(图4)。

Gsoednc

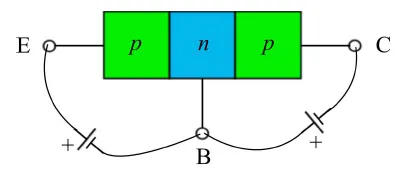
图1：共基极结构和有源区中的PNP晶体管Gsoednc

Gsoednc

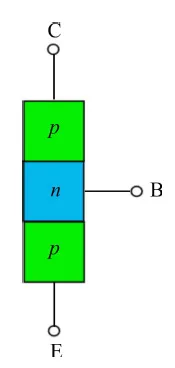
图2：+π/2的旋转Gsoednc

Gsoednc

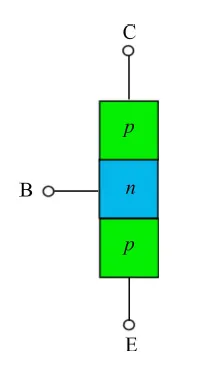
图3：空间反射Gsoednc

Gsoednc

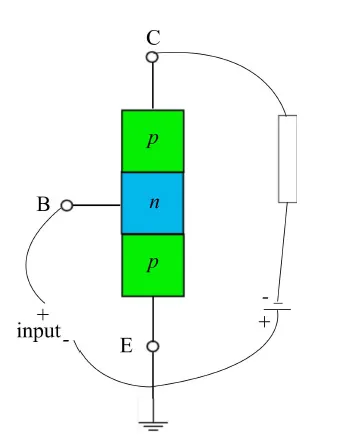
图4：复极化。矩形代表欧姆负载Gsoednc

Gsoednc

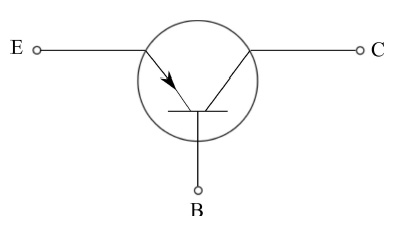
图5：PNP晶体管的电路符号(共基极结构)Gsoednc

Gsoednc

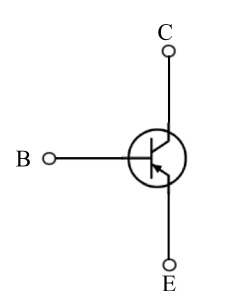
图6：PNP晶体管的电路符号(共发射极结构)Gsoednc

我们刚刚看到的是物理布局。让我们来看看那个电路图。在图5中，我们回顾了共基极PNP晶体管的符号，而在图6中，我们显示了共发射极PNP晶体管。Gsoednc

现在让我们来看看图7中所示的电路图。按照惯例，假设V_CC>0(电源电压)；输入电流为I_B，而V_CE为输出电压。由此可见，涉及的量如下：Gsoednc

Gsoednc

由于发射极充当输入和输出之间的接口，因此电流I_E不起决定性作用。所以我们在可能的自变量选择中排除这个量。基极电流I_B在功能上与输入电压V_BE相关，并且这种情况排除了这两个变量作为自变量的可能。然而，这两个量对于研究晶体管的电气行为非常重要，因此我们假设两者之一作为自变量，为此我们通常采用电流I_B。在输出网格中，我们可以找到I_C和V_CE：我们假设输出电压V_CE作为自变量。总之，(V_CE,I_B)是我们正在寻找的一对自变量。其余量的函数关系如下：Gsoednc

Gsoednc

Gsoednc

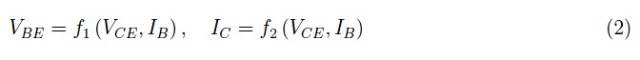
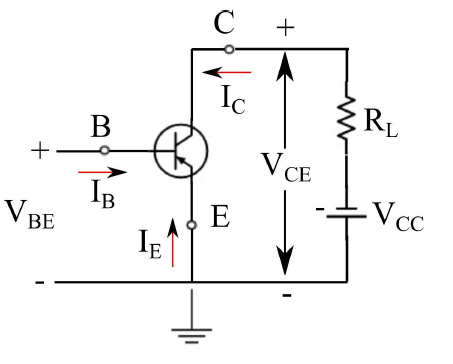
图7：PNP晶体管电路图(共发射极结构)Gsoednc

要绘制特性图，请记住，对于任何器件，我们都必须有电压与电流的关系，反之亦然。Gsoednc

在等式(2)的第一部分中，假设V_CE作为给定值范围内的可变参数，而基极电流I_B是自变量。因此，我们有了输入特性(更准确地说，一系列特性)，它告诉我们对于给定的输出电压值，输入电压如何随基极电流的变化而变化。Gsoednc

类似地，在等式(2)的第二部分中，假设基极电流I_B为给定值范围内的可变参数，而输出电压V_CE为自变量。因此，我们得到了输出特性(更准确地说，一系列特性)，它告诉我们对于给定的基极电流值，集电极电流是如何随输出电压而变化的。Gsoednc

现在让我们确定各个量的符号。根据我们对电流的定向，V_CC>0且极性如图7所示，意味着I_C<0。此外，其他电流和电压的符号均为负。明确这一点后，我们在图8中绘制了输入特性，而在图9中绘制了输出特性。在这两幅图中，我们可以看到典型的指数上升趋势。图9中，红色曲线是极限耗散曲线，即恒定耗散功率点的几何轨迹(在输出网格中)。该曲线上方的工作点对应于更大的耗散功率。Gsoednc

Gsoednc

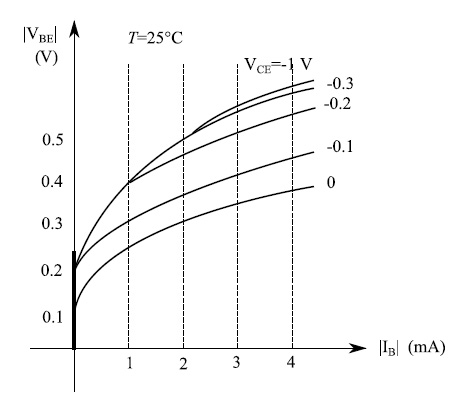
图8：PNP晶体管的输入特性(共发射极结构)Gsoednc

Gsoednc

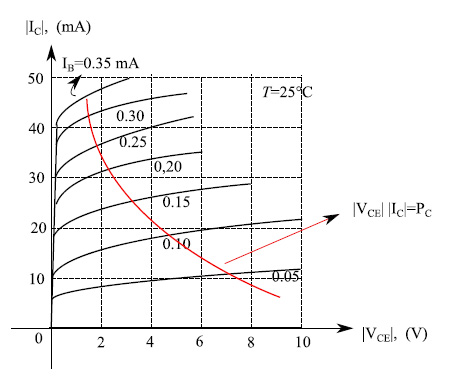
图9：PNP晶体管的输出特性(共发射极结构)Gsoednc

(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Common Emitter Configuration，由Ricardo Xie编译。)Gsoednc