
与人们普遍认为的相反,第一个半导体理论模型以及激子理论模型可以追溯到20世纪30年代。那是量子革命的黄金时代……
当然,在当时这还缺乏技术意义,以至于诺贝尔物理学奖得主W.Pauli写信给他的同事Peierls:“忘记半导体吧,它们是垃圾……也许它们甚至根本不存在”。
在之前的文章中,我们研究了可见光范围内的电磁辐射与半导体晶体之间的相互作用,尽管只是简单的研究。从现象上看,一束强度为I0(ν)的辐射束入射到厚度为d的晶体层上时,部分会被反射,部分会被吸收。吸收可以通过一个由吸收系数控制的指数阻尼来描述,吸收系数取决于频率ν,我们用µ(ν)表示,即:

由于µ(ν)取决于频率,其量纲为长度的倒数,是一个光谱量,因此可以呈现给定频段的特征值。典型值的范围为0<µ<106cm-1。对于Si/Ge(硅/锗)半导体,在可见光谱中µ(ν)≫1(对应于1.7÷3eV的能量范围),然后在红外波段急剧下降。因此,硅和锗几乎能吸收所有可见辐射。
在光电导性的研究中,我们已经看到,入射电磁辐射的能量有利于电子从价带跃迁到导带,从而破坏了共价键。
应该注意的是,这不是量子跃迁(发生在原子和分子中的那种),而是由于温度或电磁辐射而导致的一种统计机制。
然后我们仔细考虑了相应的自由电荷(电子和空穴),除了与晶格(由周期性电势而理想化的)相互作用之外,没有其他相互作用。然而,在现实的讨论中,我们必须考虑电子和空穴之间的吸引力(库仑力),即各自电荷的相反符号。实际上,我们可以考虑以下情况:
我们称这种系统为激子。由于空穴不是物理意义上的粒子,因此激子是一种准粒子,但在能量传输中发挥着重要作用,但由于它是电中性的,因此在电荷传输中不发挥什么重要作用。此类系统参与了半导体中的许多光学和光电过程。
在Wannier-Mott模型中,纯库仑势被晶体的电导率e所屏蔽,在现象上被假定为电子-空穴相互作用势,所以存在电子-空穴相对位置矢量r模的-r-1型相关关系。因此,与类氢系统有相似之处,其核是带正电荷的粒子Ze,其中Z是原子序数,e是电子电荷的绝对值。所以,我们有:

在式(1)中,严格来说,r是关于系统重心的相对核电子坐标。在类氢系统的情况下,重心实际上与原子核重合,因为与电子相比,原子核质量很大。然而,在激子中,我们必须严格假设r为相对距离,并参考重心的运动。然后,考虑到电导率,电子-空穴相互作用势可写为:

我们必须考虑表征所研究晶体的能量Eg。准确地说,通过将能量的零点放在价带顶部,我们可以得到电子的势能(从共价键中释放出来)为:

具有重要物理意义的束缚态的能量为0<E<Eg(图1):E>0意味着共价键的断裂;E<Eg意味着没有足够的能量移动到导带。
因此,我们很有可能在释放的电子和相应的空穴之间形成一个束缚态。
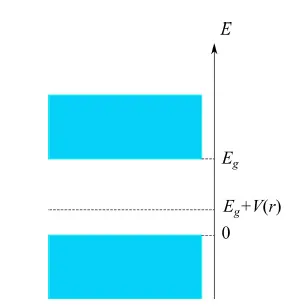
图1:电子从入射电磁辐射接收能量
此时,我们要做的就是拿一本量子力学手册来回顾一下,氢原子的能量本征值和本征函数。沿着这个思路,我们可以写出激子(氢系)的本征值或能级,如下:
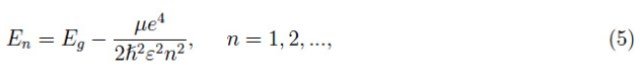
其中,μ是系统的简化质量:

其中m*e和m*h分别是电子和空穴的有效质量。表征稳态(即能级)的本征函数由量子数nlml确定。我们感兴趣的是n,因为它在(5)中标识了各个能级。结果表明,在一般能级n中,激子的“经典半径”≫玻尔半径(基态氢原子的“经典半径”,即n=1),因此也远大于晶格常数。这意味着Wannier-Mott模型对于尺寸远大于晶体晶格常数的激子是有效的。
能级的排列如图2所示。显然,n=1是基态,而n=+∞的状态对应于电子处于导带的电离。我们要记住,我们是在重心静止的系统中工作,因此我们必须考虑平移运动的能量,由于系统的动量通过多个波和简化的普朗克常数来量子化地表达。准确地说,我们有:

该能量未量子化,因此在能级谱中(图2)会出现每个能级En的状态的连续体,每个状态都被称为激子带。
如果系统不受外部场的影响,重心最多只能做直线匀速运动。换句话说,我们的电子-空穴键合系统,在所做的假设中,最多只能做平移运动。
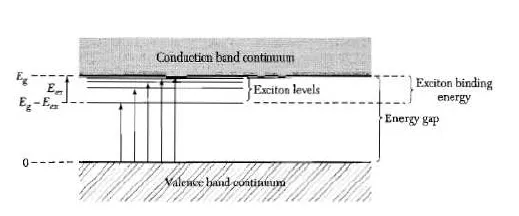
图2:激子的典型能级图(来源:《固体物理学导论》,C. Kittel)
在这个近似的顺序中,我们忽略了自旋。请记住,电子和空穴都是自旋为1/2的系统,总自旋为S=0(单重态)或S=1(三重态)。由此可见,S将出现在量子数nlml旁边。准确地说,如果自旋态是单重态,我们将讨论副激子;如果自旋态是三重态,我们将讨论正激子:与单重态相比,三重态在能量上受到抑制。
实验结果表明,在T=4K时硝基氧化铜的光谱中,发现了类氢系列:
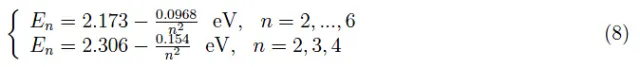
双系列的出现是由于导带和价带的复杂性,因为类型(5)的类氢系列是在理想抛物线带模型中获得的。顺便说一句,关于激子态的早期研究工作主要集中在更现实的模型上。
由式(5)可得电离能:

其中:

是结合能。与氢键能(EB(H)=13.6eV)相比,我们有:

其中m是自由电子的质量。Ge/Si半导体的典型值为µ∼0。2,ε∼16,由此EB= 0.016eV,这个值明显低于室温下的热激发能。因此,除了在低温下之外,Ge/Si不适合激子的形成。相反,氧化亚铜和硫化镉等半导体即使在室温下也具有良好的激子浓度。
从实验的角度来看,从一个能级到另一能级的转变很有趣,并伴随着光子的吸收/发射。然而,调节这些过程的量子机制很复杂,因为它涉及到声子。因此,这超出了本文的讨论范围。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Wannier–Mott Excitons in Semiconductors,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯