
我们在图1中展示了一个长度为L的pn结的电荷载流子(电子/空穴)势能图(在上一期中进行了研究),该结具有开路和不对称耗尽层。V0>0是为两个电荷载流子产生双势垒的内建电势。Wn,p表示给定x下的单粒子势能值。其结果是不存在电荷的净流动。
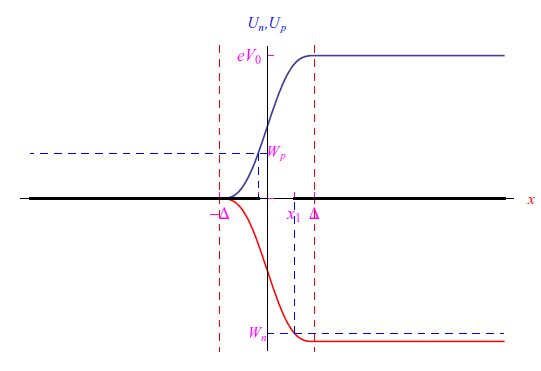
图1:双势垒。粗水平线定义了两种电荷载流子允许值的横坐标
在反向偏置条件下,施加在结上的电压V<0会导致两个电荷载流子的势垒eV增加,其中e是电子电荷。由于势垒升高,空穴向左侧扩散,电子向右侧扩散,从而使离子电荷未被覆盖,因此耗尽层也随之扩张(图2)。这种扩散过程注定会减弱,因为要使其静止,需要从n区提供空穴,而在n区名义上是不存在空穴的。类似的论点也适用于电子。
理想情况下,图2的电路中没有电流流动。在更现实的情况下,单个区域内的少数载流子会发挥作用,因此会出现我们所要讨论的反向饱和电流,其绝对值为i0(在μA量级),i0(T)会随着少数载流子的热产生而单调增加。在之前的文章中,我们已经为i0(T)建立了一个有效的经验法则,尤其适用于锗和硅。
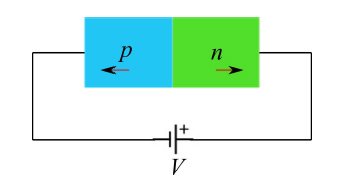
图2:反向极化后多数电荷载流子的瞬时扩散
从量子统计力学来讲,我们有:
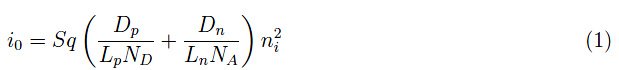
对于方程(1)第二部分的各个量:S为接点的横截面;q是电子电荷的绝对值(这并不是符号的滥用,之前我们使用的是符号e,不幸的是,它与进入因子ni的自然对数的底数相冲突);Dp、Dn为扩散常数;Lp、Ln是与电子和空穴相关的特征长度。一般来说,如果我们有一个平均寿命为τ的带电粒子的扩散常数D。那么粒子在湮灭前所行走的平均长度由以下公式给出:

其中ND,NA是我们已知的符号:供体和受体原子的浓度。因子ni2源自质量作用定律np= ni2,它与本征半导体中电荷载流子的浓度有关。准确地说,我们有:
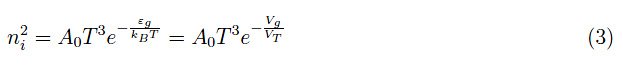
其中A0是一个常数,包含电子和空穴的有效质量,而εg是禁带宽度,通常以eV为单位。我们可以证明最后一步的合理性:通过定义电势Vg=εg/q,我们可以得出Vg在数值上等于禁带宽度(请记住,1eV是电子在1V的电势差作用下加速所获得的动能)。
对于锗和硅,扩散长度为T-1([2])。然后由方程(1)得出:

其中K是一个常数。到目前为止,我们忽略了耗尽层中电荷的生成/重组过程:这是一种由于晶格节点中仅存在静止离子而产生的理想情况。这种理想条件对锗有效,但对硅无效。正如在结的电压-电流特性中已经看到的那样,最好通过一个无量纲量η来对这种理想状态的偏差进行参数化,其中对于锗η为1,对于硅η为2(只在小电流下,对于较高电流,耗尽层中的生成/重组可以忽略不计)。根据上述的考虑,可对方程(4)进行推广:

各个系数和禁带宽度(以伏特为单位)为:
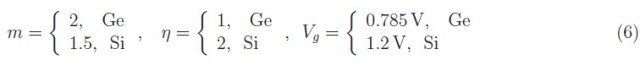
在图3中,我们以半对数标度报告了锗和硅的i0/K变化趋势。
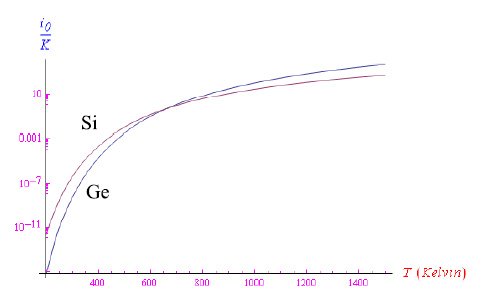
图3:i0/K随绝对温度变化的趋势
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: The Dynamic Role of the Reverse Saturation Current,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯