
蒙特卡罗分析是电子仿真中使用的一种技术,用于使用随机参数进行一系列仿真。该技术利用了随机性,它的名字灵感来源于著名的蒙特卡罗赌场。在电子仿真中,蒙特卡罗分析用于评估电子元件(电阻器、电容器、电感器等)和工作条件的变化对电路的影响。换句话说,仿真运行多次,每次都要对所考虑的参数设定一组随机值。这些随机值可通过代表元件值变化的概率分布来获得。
通常,电子仿真使用电子元件的恒定值。实际上,由于每个电子元件并不理想,外部工作条件也总是不同,因此这些值可能会有变化。例如,电阻器的标称值为100Ω,偏差为5Ω,蒙特卡罗仿真会考虑从平均值为100Ω、偏差为5Ω的正态分布中随机抽取值,因此随机值在95和105Ω之间。比如说,使用偏差为5Ω的100Ω电阻器对电路进行蒙特卡罗仿真可能会生成以下电阻值:96、102、100、97和103Ω。
蒙特卡罗分析可用于估计元件值变化对电路行为的影响。它对于评估具有公差或不确定性的组件的系统特别有用。蒙特卡罗分析可用于改进电路的设计,提高其可靠性。为此,可以设计电路,使其行为即使在最极端的条件下也能满足所需的规格。由于元件值的变化是随机的,这种类型的分析提供了更真实的仿真系统结果。它涉及大量的仿真分析,其中每个元件的值都在所需范围内随机变化。随机生成算法应保证尽可能高的随机率。
图1显示了由以下元件组成的经典电源图:
该方案使用4个1N4007二极管,其SPICE模型如下:
model 1N4007 D(IS=7.02767n RS=0.0341512 N=1.80803 EG=1.05743 XTI=5 BV=1000 IBV=5e-08 CJO=1e-11 VJ=0.7 M=0.5 FC=0.5 TT=1e-07 type=silicon)
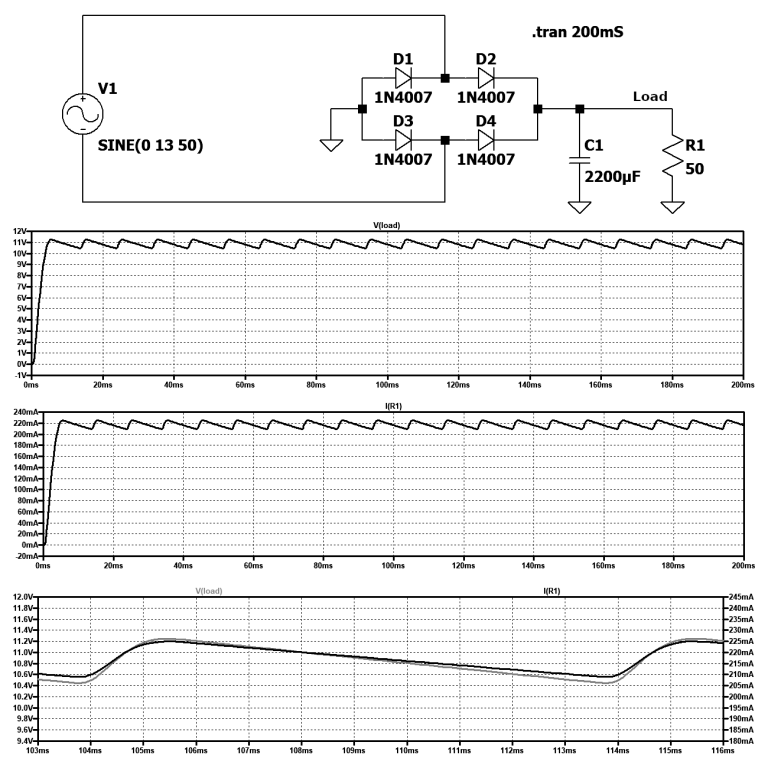
图1:经典低压电源
该图显示了四个要素:
在示例图中,假设元件值是理想的。在这种情况下,该图表也是理想的,并且没有考虑到电子元件,特别是电解电容器可能的变化。使用LTspice提出的示例的NETLIST如下:
* Montecarlo – by Giovanni Di Maria
V1 N001 N002 SINE(0 13 50)
D1 0 N001 1N4007
D2 N001 load 1N4007
D3 0 N002 1N4007
D4 N002 load 1N4007
C1 load 0 2200µF
R1 load 0 50
.model D D
.model 1N4007 D(IS=7.02767n RS=0.0341512 N=1.80803 EG=1.05743 XTI=5 BV=1000 IBV=5e-08 CJO=1e-11 VJ=0.7 M=0.5 FC=0.5 TT=1e-07 type=silicon)
.tran 0 100mS 0
.backanno
.end
所有分立元件均可在市场上购买到,公差为1%、5%、10%、20%等。此外,电容器还具有极高的弹性值,有时甚至与元件本身标注的值相差甚远。工作温度也会严重影响器件的固有值。由于这些原因,设计人员需要一个更真实的图表,可以研究所用组件值的真实变化,以便他们可以观察系统的真实行为。因此,假设电解电容C1的容差为50%,则电容值可在1100 uF至3300 uF之间。电容和所有其他组件的变化都必须同时处理,并且可能的理论运行条件组合非常多。为了生成随机值,我们使用mc(value, tolerance)函数。其语法如下:
mc(x,y)
它会随机生成一个x*(1+y)和x*(1-y)之间的均匀分布值。LTspice电路图中包含的指令如下:
.param Capacitance=mc( 2200u , 50/100 )
.step param Simulations 1 10 1
在这种情况下,电解电容器C1不得为2200uF的固定值,而必须包含变量后缀{Capacitance},这样模拟器才能始终在指定范围内为元件分配不同的值。变化区间也可以输入为十进制数,而不仅仅是分数。在图2所示的电源仿真中,根据电解电容器的不同电容,显示了不同的纹波率。
下图突出显示了信号的一个周期的缩放。为简洁起见,仿真只进行了十次,但建议执行更多次,特别是当要改变的电子元件很多时,但要考虑到仿真时间以及所需的PC内存会随着步数的增加而成正比增加。仿真中会生成十个不同的值。正如您所看到的,图表显示了不同的曲线,并且元件值的变化使我们了解了元件是如何显著影响和改变电子电路的行为。在图中,值得注意的是,位于6ms处的时间点不受电解电容值的影响。可以说,该点每10ms被定位一次,该值很容易从50Hz信号的半周期持续时间推导出来。
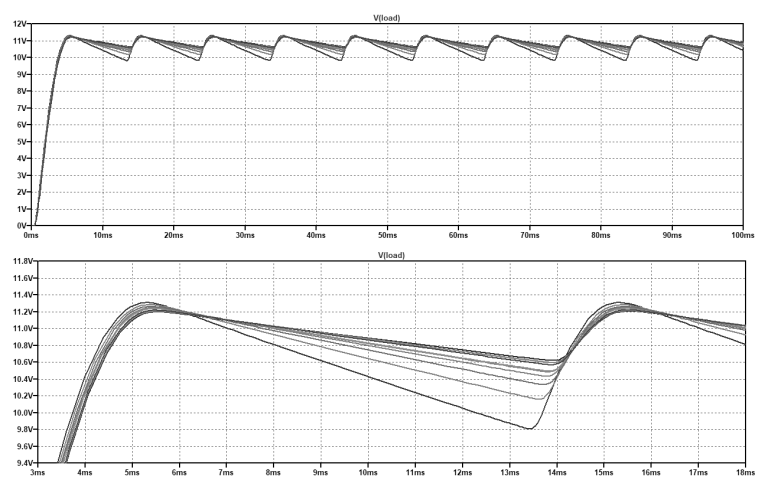
图2:具有不同电解电容器值组合的电源的电子仿真
温度也可以受到随机变化的影响,以便与其他组件的变化一起得到很好的仿真。蒙特卡罗温度分析的一个典型示例是观察配置为共发射极放大器的晶体管。在共发射极放大器中,输出电流与输入电流成正比。电路图采用双电阻配置,这是一种故意受热漂移影响的解决方案。然而,两个电压之间的关系受到多种因素的影响,包括温度。温度会影响晶体管的特性,这些变化可能会导致放大器出现故障。
温度蒙特卡罗分析可用于估计温度变化对电路行为的影响。为此,需要运行大量电路仿真,每个仿真都有不同的温度。仿真结果可用于创建放大器输出电压和电流的概率分布。该分布可用于确定输出值大于某一特定值的概率。温度蒙特卡罗分析是一项重要技术,可用于改进电子电路的设计和定值。运行仿真后,结果将被用于创建电路中节点处所有值的概率分布。图3显示了该放大器的电路图,其增益约为400,与1kHz的正弦信号和10mV的幅度相关。晶体管温度的升高可能会变得危险,并导致集电极电流增加,直至出现雪崩效应。假设您想在蒙特卡罗仿真中测试0°C到60°C之间的温度。要设置的指令如下:
.param T=mc(30,100/100)
.temp {T}
.step param Simulations 1 10 1
第一个指令的目的是为变量T分配一个介于……和……之间的温度值:
30 – (30*100/100) = 0°C
30 + (30*100/100) = 60°C
第二条指令有效地将温度设置为变量T的值。最后,第三条指令执行十次仿真,不时改变温度值,但始终在设定区间的范围内。
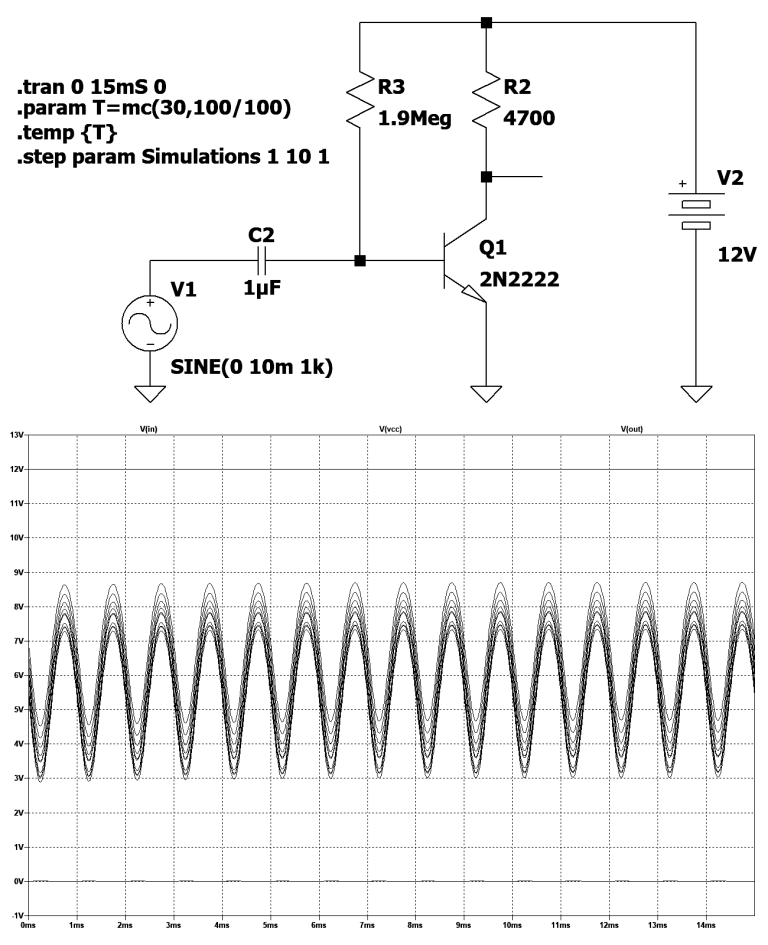
图3:在动态条件下,晶体管集电极上的电压随温度的变化
通过恰当的操作,可以随机改变所有可以想象到的元件电气参数。通常,电子仿真是完美且无错误的,指定了唯一且精确的值,但使用蒙特卡罗方法可以提高测试的真实性,从而使仿真电路的行为更接近真实电路。利用这种方法,可以观察当电子元件的值处于允许的最小和最大极限时的系统的行为。仿真结果通常以所用值的概率分布的形式呈现。
该技术在设计阶段非常有用,因为在设计阶段评估电路在电子元件值不确定的情况下的鲁棒性和可变性非常重要。在这种类型的仿真中,进行的测试次数越多,最终结果就越好,尽管这会大大增加处理时间和因临时文件的存在而占用的硬盘空间。最后,当要处理的变量数量较多时,蒙特卡洛仿真尤其有用。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Guide to Spice Simulation for Circuit Analysis and Design – Part 10: Monte Carlo Analysis,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯