
在之前的文章中,我们讨论了决定pn结反向饱和电流随温度变化而呈上升趋势的物理机制。在本文中,我们将研究所有极化的热效应。
在研究pn结中电流随温度(正向偏置)变化的行为之前,我们先对反向饱和电流的变化趋势进行分析论证,并遵循以下符号惯例:
v、i……等小写字母表示随时间变化的量。大写字母V、I……表示固定量,最多是参数变量的。
之前文章中找到的反向饱和电流的解析表达式如下:

为了方便起见,我们再次列举一下锗(Ge)和硅(Si)的实验数据:
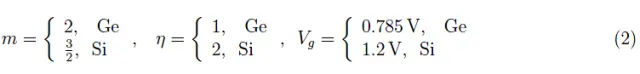
方程(1)是变量T的函数,而不是外加电压V的函数,因为除非存在不可避免的击穿,否则反向饱和电流与V无关。函数(1)的一阶导数很容易计算,同样直接的对符号研究,从中可以清楚地看出I0(T)是一个单调递增函数。
有鉴于此,正向偏置热行为的研究在分析上更加复杂,因为电流是实变量(T,V)的非负实值函数:

其中a=1/11600(V/K)。I0电流的增加会导致正向偏置电流的增加。这并不奇怪,因为导致I0增加的物理过程从根本上说与少数载流子浓度增大有关,而这一过程在正向极化中也很活跃。
函数I(T,V)没有相对极值点,因为它的梯度始终不为零(I(T,V)关于V的偏导数是微分电导,始终为正)。图1中的I(T,V)图很有启发性,在图中我们可以看到电流随温度变化而增加的趋势,即图中与垂直于纵轴(电压)的平面相交的部分。在图2中,是在更宽的外加电压范围内的相同函数的图。我们可以研究以V为参数的I(T)的行为:我们对I(T)的单调性特别感兴趣,这相当于确定方程(3)关于变量T的偏导数的零点。不幸的是,由此产生的方程无法以封闭形式求解,因此在下一节中,我们将依靠计算分析。
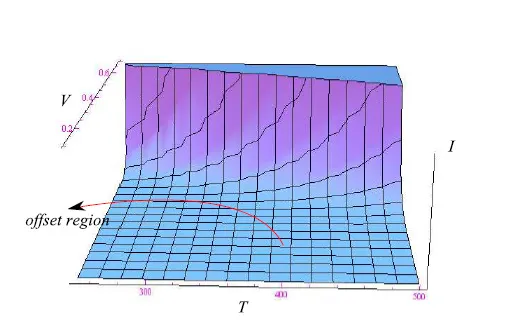
图1:函数I(T,V)(方程(3))图,其中T在适当范围内变化,而V在0至0.7V之间变化。对于给定的V值,请注意电流随温度变化呈上升趋势的偏移区域。
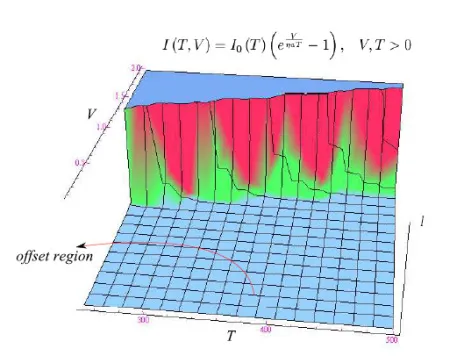
图2:T的函数I(T,V)(方程(3))图,其中T在适当范围内变化,而V在0至2V之间变化
我们提出了一种计算分析方法,通过绘制电流(3)与正向偏置电压V的指定值的温度函数关系图来确定I(T)的增加/减少。为此,我们必须指定温度范围Tmin以及Tmax=500K,未表达最小温度值(最大值500K纯粹是理论值,从实验的角度来看,我们参考350K的阶跃值)。由计算分析可知,当V值远小于Vg时,电流I(T)是严格递增的函数;当V略高于Vg,存在一个温度T*,使得当Tmin≤T<T*时,函数I(T)单调递减,而当T*<T≤Tmax时,I(T)为单调递增。换句话说,T*是I(T)的相对极小点,我们用V*表示V的预测值,但要注意(T*, V*)不是函数(3)的最小点。不过,我们预计T*以及V*与Tmin有关。
通过将结与液氮恒温器热接触(Tmin=77K),然后在逐渐升高的温度下使用恒温器,对于锗,我们获得了图3的趋势。
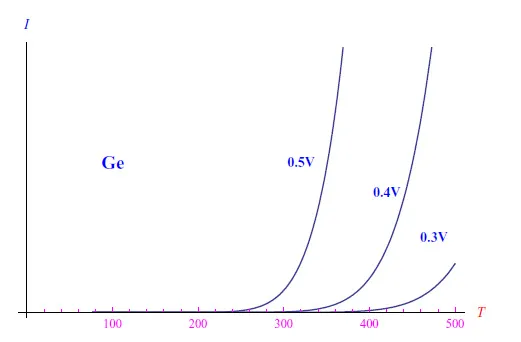
图3:对于给定的外加电压V,直接极化电流随温度变化的趋势(锗的情况)
77K的选择并不是随意的,因为了解使用其他形式掺杂的低温下pn结的行为非常重要,在此范围内,结往往表现得像绝缘体,这代表了严重的技术限制(想想太空探测器上的设备)。
对于Tmin=77K,结果为T∗=81.2K,V*=0.799V,如图4所示。我们观察到T∗接近最低温度77K,因此在实验上意义不大。然而,我们用Mathematica验证(T∗, V*)不是函数I(T,V)的相对/绝对最小值点。正是通过ContourPlot指令,我们绘制了I(T,V)函数的电平曲线,即I(T,V)取常数值的TV坐标平面的曲线。图5显示,曲线并未在点(T∗, V*)附近闭合,而是在相对最小值或最大值的点处闭合。
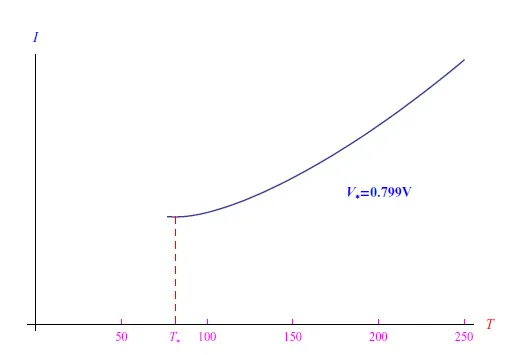
图4:V=0.799V时,直接极化电流随温度变化的趋势 (以锗为例)
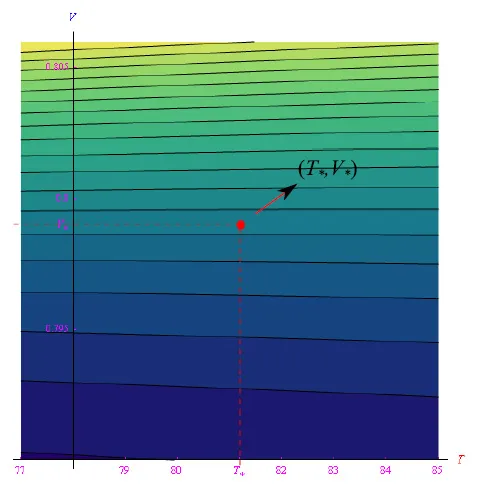
图5:函数I(T,V)在(T*=81.2K,V*=0.799V)邻域的一些电平曲线
为了在实验中确定电流趋势发生逆转时的温度T*,我们从V*=0.799V开始对电压V进行小幅增加。例如,对于V′=0.82V我们得到如图6所示的趋势,从中我们看到T′=203K。由此可见,随着V的增加,I(T)的极小点向横坐标增大的方向移动。这相当于说函数T*(V)是单调递增的,因此将存在一个值Vcrit,其中T*(Vcrit)>Tmax。由于这是一个超出范围的温度,因此对于V≥Vcrit,电流会随着属于观察范围的T值增加而减小。对于锗,计算分析得出的值为Vcrit=0.87V(图7)。就电平曲线而言,图8中的图形显示了两个点(T*,V*),(T′,V′),证实了之前的分析,根据该分析,作为偏置电压V,逆转温度趋向于V增加的方向。上述一对点是电流关于温度T的偏导数的两个不同的零点。
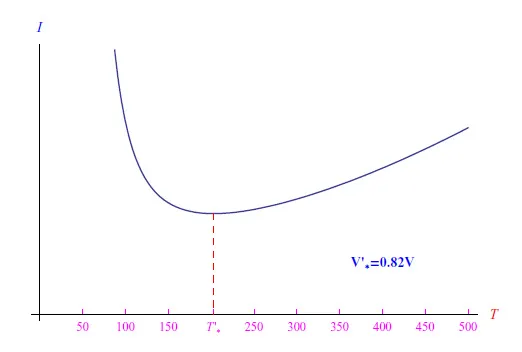
图6:V=0.82V时直接极化的电流趋势与温度的函数关系 (以锗为例)
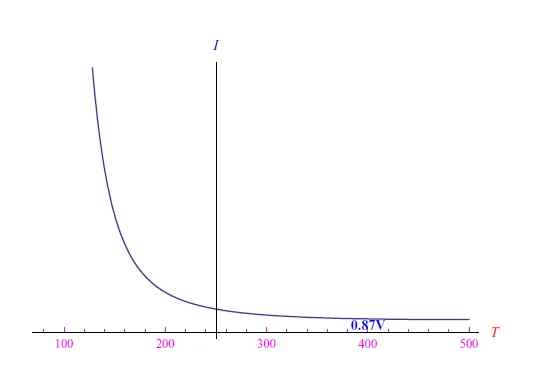
图7:V=0.87V时直接极化的电流趋势与温度的函数关系(以锗为例)
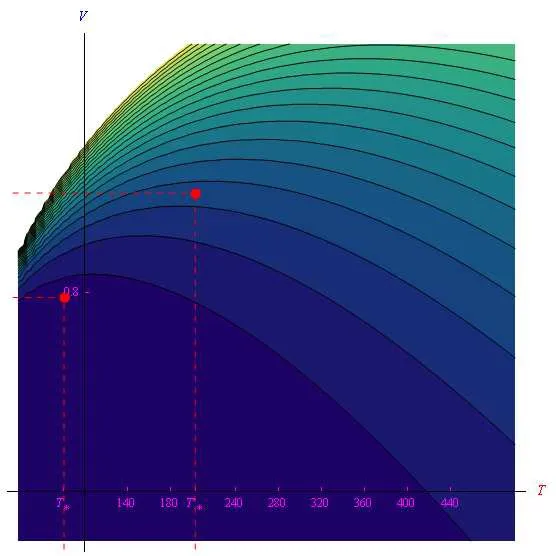
图8:函数I(T,V)在I(T,V)对T的偏导数的两个不同零点附近的一些电平曲线
最后,我们注意到,随着Tmin值的逐渐减小,相应的V*也会减小。Tmin→0的极限是V∗→Vg,即以伏特为单位的禁带宽度。我们认为这一形式上的结果意义重大,应在亚微观尺度上研究这一奇特巧合的原因。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Thermal behavior of a PN junction,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯