
在许多研究pn结电流随温度变化行为的实验室实验中,反向饱和电流通常被假定为常数。这只是一个近似值,因为这个量与温度有很大关系。在更现实的情况下,我们建议在Mathematica计算环境中进行虚拟/计算实验。
在之前的文章中,我们看到在温度T时,处于热力学平衡状态的pn结在电势差V下的电流为:

其中a=1/11600(V/K)(对于锗):

这里,Vg=0.785V(禁带宽度以伏特为单位),而K是一个正常数。从方程(1)中我们可以看出,I0(T)是V→-∞时反向饱和电流的绝对值。
由于方程(1)第二项指数的快速阻尼作用,在室温下,I0(T)的值将达到|V|,也就是70÷80V的数量级。
为了确定常数K,我们通常使用二极管制造商提供的数据:
I0(Tamb),其中Tamb是环境温度。对于锗,Tamb=298.15K(相当于22°C)时的典型值为1µA。根据方程(2),以恰当的计量单位计算,K=206.638。当然,这个值与温度无关,因为K是一个常数。
现在,我们可以重建指定二极管的电压-电流特性。在室温下,我们可以看到图1所示的趋势,从图中我们可以看出,由于二极管的电阻较小,电流达到了令人望而却步的数值。让我们记住,理想情况下,二极管在正向偏置时表现为短路。为了限制电流,我们插入一个电阻负载,如图2所示。
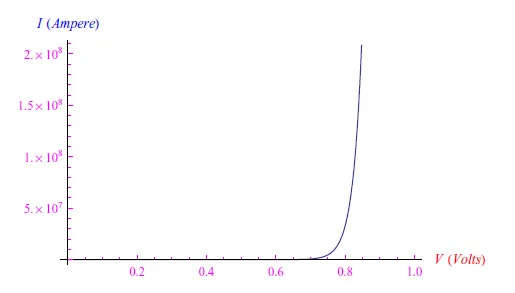
图1:电压-电流特性(T=Tamb时的函数(1)图)
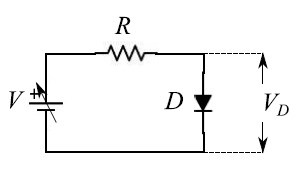
图2:通过在二极管上串联一个电阻负载来限制电流强度。串联负载由可变电压发生器供电
在对图1中的电路进行分析讨论之前,我们注意到,从实验角度来看,除了前面提到的温度Tamb外,下列温度也很有趣(小写表示温度,单位为℃):
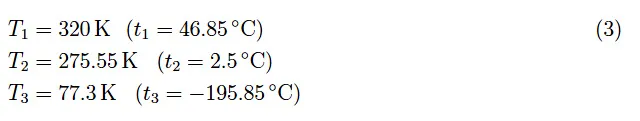
因此需要四个恒温器。第一个是环境温度的;第二个是水热量计(温度T1);第三个是水冰融化热量计(温度T2);第四个是液氮热量计(温度T3,即1标准大气压下的液氮沸点)。由于这些都是水恒温器,因此测量电路部分(电压表、电流表)必须适当进行防水处理。
将基尔霍夫第二原理应用于图1电路的单链路,结果如下:

其中,VD是二极管两端的压降。电流I由(1)得出,用VD代替V。因此,我们可以得出:

对于给定的V值和T=Tk(方程(3)),刚才所写的方程构成了一个未知数系统(I,VD),从中很容易得到:
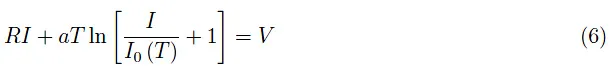
在给定V值的情况下,这是一个需要数值求解的超越方程,涉及到I,温度T在该V值情况下取(3)式中的一个值。因此,可以使用任何传统编程语言(如Fortran)在软件中重建I(T,V)。
不过,利用CAS(计算机代数系统),我们可以在不进行数值分析的情况下强制求解(6)式。例如,Mathematica可以通过Lambert函数来表达解。
请注意,给定T值时I(T,V)与V的函数关系图并不是二极管的电压-电流特性,因为后者是压降VD的函数,而压降是方程组的第二个未知数。一旦已知这两个量,我们就可以用Mathematica建立一个元素分别为VD和I的有序对列表,然后绘制它们的图形。
例如,对于T=T1=320K和R=1kΩ,我们可以得到图3中的趋势。对于T=T3=77.3K,我们可以得到图4所示的趋势图。请注意,电流范围保持不变,而VD范围却有所增加。这意味着电流随着热量的降低而减小。
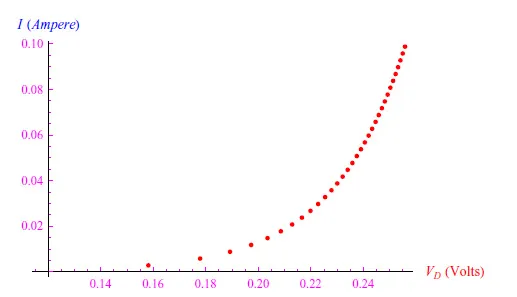
图3:T1=320K时电流强度随VD变化的趋势。R=103Ω
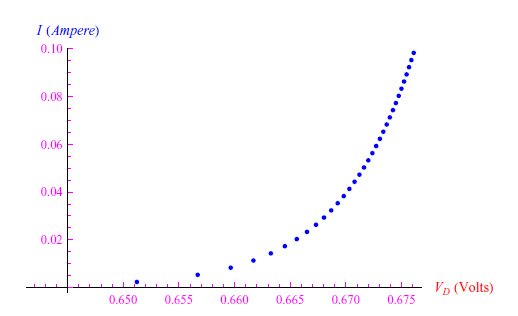
图4:在T2=77.3K时,电流强度随VD变化的趋势。R=103Ω
考虑到反向饱和电流与温度无关,方程(6)变为:
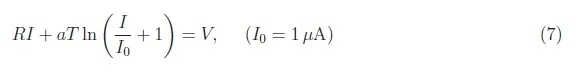
使用Mathematica重复上述过程后,我们发现T = T1时的电压-电流特性(VD, I)与精确解差别不大,因为该温度略高于室温(精确解与近似解一致),而T=T3=77.3 K时的电压-电流特性(VD, I)与精确解差别明显,如图5所示。为了使这种差异更加明显,我们在图6中以对数标度报告了两种解法(精确解法和近似解法)的变化趋势。
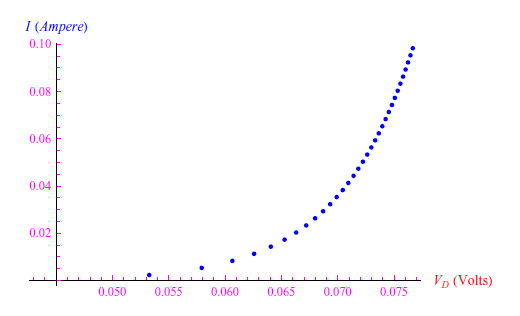
图5:假设反向饱和电流恒定,T3= 77 K时电流强度随VD变化的趋势
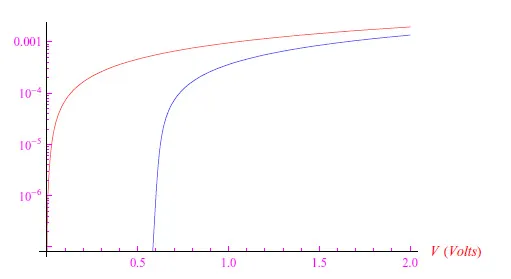
图6:蓝色曲线是电流强度与V值的函数关系,计算时考虑了反向饱和电流与T值的关系。红色曲线是近似解,即电流强度与V值的函数关系,计算时假定反向饱和电流与温度无关。
从物理角度看,图6所示的各个解决方案(精确和近似)的趋势与预期完全一致,因为随着温度的降低,pn结各区域的少数载流子浓度会逐渐降低。这导致了反向饱和电流的减小,因此也导致了正向偏置电流的减小,因为反向电流对正向电流也有影响,这在之前的研究中已经有所体现。因此,认为I0与温度无关是不现实的。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: virtual experiment on the thermal behavior of a PN junction,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯