
Mathematica计算环境除了允许通过软件添加掺杂原子来执行半导体掺杂虚拟实验之外,还实现了一种区分半导体和金属行为的计算标准。
为了方便起见,我们使用了之前文章中已经找到的关于本征半导体导带中电子数量Ne(T)以及导带价态中空穴相对数量Nh(T)的方程。根据符号的含义,我们有:
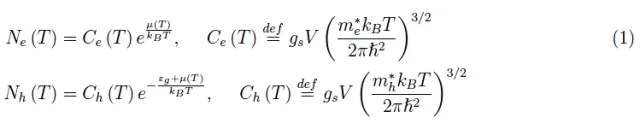
在此基础上,通过施加电中性条件,就可以得到化学势:
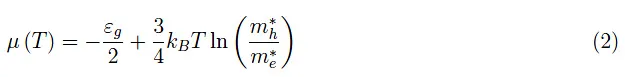
随着五价杂质的添加,总电荷构型变得更加复杂,因为现在不仅来自断裂共价键的电子会对Ne(T)做出贡献,而且分布在供体能级中的电子也参与其中,因此能量−εd<0(图1)。
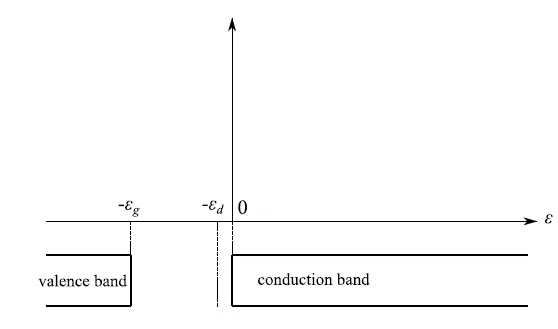
图1:−εd是五价原子价电子的能级。事实上,我们有一个极其密集的能谱,其中各个能级最多由两个具有反平行自旋的电子组成
换句话说,Ne(T)是两种贡献的总和:第一个等于Nh(T),即释放的空穴数量(每个空穴对应一个电子)。相反,第二个与正电离供体原子的数量nd(T)一致。我们可以写成:
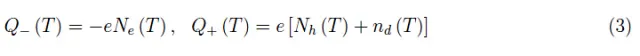
其中,Q-(T)和Q+(T)分别是温度T时的总负电荷和总正电荷,其中e是电子电荷的绝对值。由于半导体的总电荷为零,因此上述两个量必须相等:
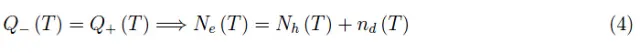
Ne(T)和Nh(T)已经从方程(1)中得知。为了确定nd(T),我们首先要注意nd(0)=0,因为供体的电离是以热能为代价发生的。“可用”电子总数,即可以从供体原子传递到导带能级的电子的总数,等于这些杂质的总数,因为每种杂质只能提供一个可用电子。设这一数目为N(0)。在温度T>0时,一定数量的供体原子电离,我们用Nd(T)表示尚未电离的原子数。但Nd(T)也是仍与各个供体结合的电子数。考虑到费米-狄拉克分布函数fe(ε),我们有:
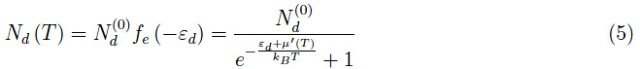
其中µ'(T)是多余电子的化学势(每个电子都属于单个供体原子)。扩散平衡时µ'(T)=µ(T),即导带中来自断裂共价键的电子的化学势。所以,我们可以写出:
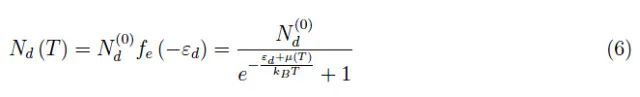
由此可知,正电离的供体原子的数量或同样的从供体原子传递到导带的电子数量,由下式给出:
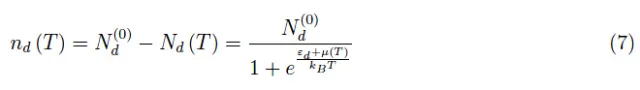
将(1)-(7)代入(4),可得:
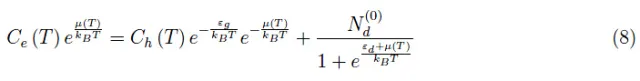
这是一个未知µ(T)中的函数方程。请注意,对于N(0)=0,我们可以得到该方程的解析解(方程(2))。另一方面,(8)式第二项中第三项的存在破坏了分析求解的可能性,因此我们必须采用数值方法。在Mathematica环境中编写例程之前,让我们先来了解一下(8)式的物理意义。在之前的文章中,我们对退化参数做了如下定义:

它量化了费米气体行为与玻尔兹曼统计量的偏差。在(9)式中,我们用z(T) 变量重新定义了这个量,即所谓的逸度。(8)式变为:
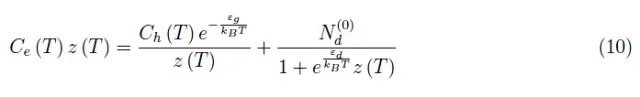
必须对z(T)进行数值求解,然后确定化学势µ(T)=kB T ln z(T)。如果半导体温度不是很高,我们有:

与第二项相比,(10)式的第二项的第一个项可以忽略不计。从物理上讲,这意味着在式(11)所设定的温度范围内,半导体中只有供体电离过程是活跃的。随着温度升高,价键断裂的过程被激活,电子随之向导带跃迁。从数学上讲,这意味着(10)式的第二项中的第一项不再可以忽略不计。
温度进一步升高会导致所谓的耗尽,即所有供体电离。在较高温度下,第一项占主导地位,即从价带到导带的跃迁是主要过程,并且半导体的行为与未掺杂的半导体类似。
在式(11)设定的温度范围内,忽略右侧第一项,解析求解方程:
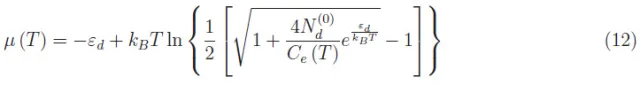
或者,对于给定的T值,我们必须针对z(T)对(10)式进行数值求解。为此,我们用1cm3的硅作参考,在(1)式的系数Ce(T)、Ch(T)中,体积V是统一的。此外,gs=2(电子和空穴的自旋自由度)。关于其他量,我们列举了掺磷的硅的数据:
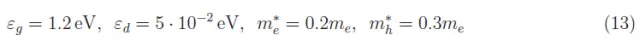
其中me是电子质量。
Mathematica计算环境使我们能够在假设N(0)作为自由参数的情况下对(10)式进行数值求解。例如,我们可以仅添加一个磷原子,从而得到图2中的趋势,其中我们将数值解与在不太高的温度下有效的解析解(方程12)进行比较。我们的模型虽然涉及技术上无法达到的温度,但仍然具有指导意义,因为它使我们明白,在添加单个磷原子后,化学势在T=10K时的值为-0.02eV,即接近导带,因此比没有杂质时的值-0.6eV(即禁带宽度的一半)要大得多。
这种行为符合化学势的定义,根据该定义,该量是在所研究的热力学系统中添加粒子后能量的增加。随着温度升高,磷原子发生正电离,电子进入导带。化学势不断减小直至达到最小值,然后单调增加。然而,解析解的图形保留了单调递减的特性(虚线),因为在该温度范围内,能够得到的解析解的近似值不再有效。需要注意的是,化学势不会渐近稳定在禁带中间,因为电子和空穴具有不同的有效质量(参见方程2)。顺便说一句,如果在我们的方程中我们假设上述有效质量相同,我们就会得到图3中的图形,从中我们可以看到化学势渐近稳定在禁带中间处。在这两种情况下,这种渐近行为都证实了前面所说的,即对于非常高的温度,电子从价带到导带的跃迁过程占主导地位。
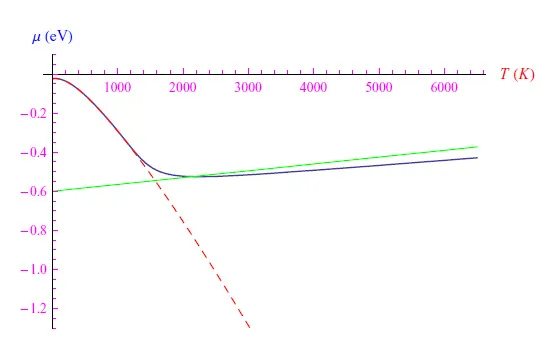
图2:蓝色曲线是(10)式的数值解图。虚线是函数(12)的图形。绿色曲线是没有杂质时μ(T)的图形(方程(2))
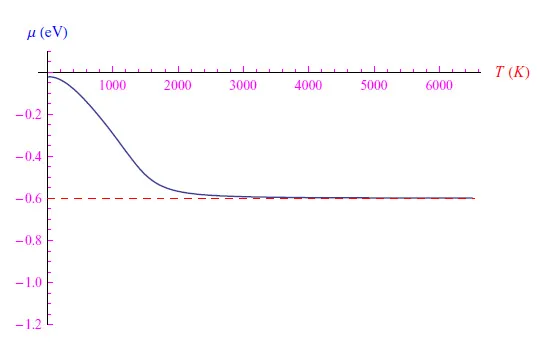
图3:如图2所示,不同之处在于现在电子和空穴具有相同的有效质量
通过添加N0=3个磷原子,我们得到了图4中的趋势,其中我们看到从T=10K开始,化学势单调增加直至Tmax=79.94 K的相对最大值,其值为-0.02 eV,然后再次下降,其趋势与N(0)=1时类似。
随着温度升高,相对最大点Tmax向横坐标增大的方向移动,即Tmax是掺杂原子数N(0)的单调递增函数。最大值µmax=µ(Tmax)也被证明是N(0)的单调递增函数,因此将存在一个温度T∗max使得µ∗max=µ(T∗max)>0。从物理上讲,正化学势是金属电子气的特征。我们得出的结论是,在给定的温度范围内,掺杂半导体的行为类似于金属。
从数值上看,对于N(0)=36,我们有T∗max=331.172 K,μ∗max=10−4eV(非常小但仍为正值);这意味着函数µ(T)存在一对零点:T1 = 303.614 K,T2 = 359.356 K。
通过将掺杂水平提高到N(0)=3·102,我们得到了图4中的趋势,从中我们通过数值确定:
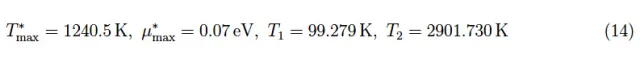
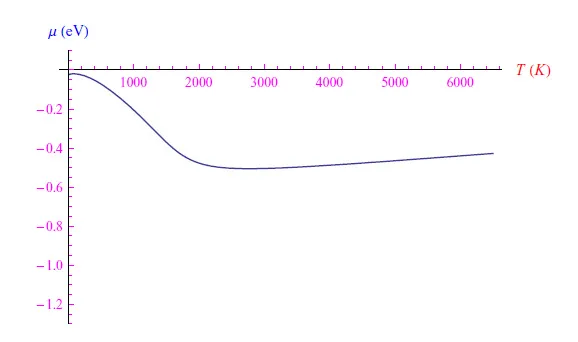
图4:N0=3个磷原子的化学势趋势
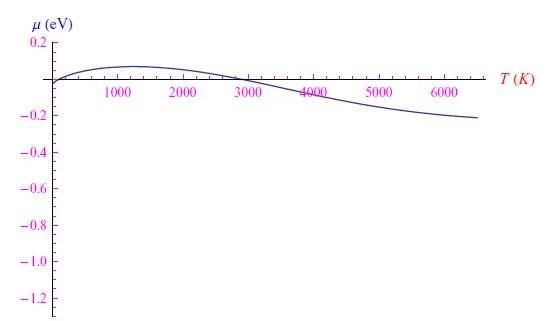
图5:N0=3·102个磷原子的化学势趋势
本文提出的计算模型是启发式的,因此与现实实验并不十分接近。我们看到,即使杂质浓度较低,也会出现金属类的行为。不过,从定性的角度来看,这一点非常重要,因为它让我们明白,添加高浓度的杂质在技术上并不有利。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: from semiconductor to metal,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯