
从确定AlGaN/GaN异质结构中的电子浓度到计算高电子迁移率晶体管(HEMT)中的AlGaN/GaN的电流密度,对费米-狄拉克积分的研究十分有意义。
在所有半导体(本征半导体或外征半导体)中,导带中的电子数由下式给出:
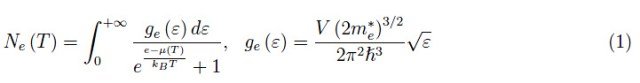
其中,ge(ε)是态密度(也考虑了自旋自由度)。正如前面的文章所确定的,在半导体中,电子气是非退化的。这种情况在数学上可以转化为经典极限:

这样我们就可以对积分(1)进行近似计算,因此电子浓度为:
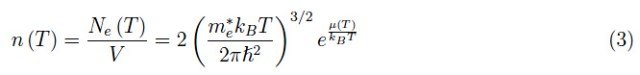
考虑方程(2),我们有:

因此,导带中的电子气体极度稀疏。这并不奇怪,因为在相反的情况下,由于单电子波函数的叠加而产生的量子效应不再可以忽略不计,从而导致与经典行为的偏差,并因此导致气体的退化。这些论据表明,方程(4)的第二项就是量子浓度。所以:

我们得出的结论是,在半导体中,电子浓度永远不会超过量子浓度。更准确地说,当n(T)>nc(T)时,电子气会失去稀疏性,半导体的行为会趋向于金属。我们是从确定化学势µ(T)的数值仿真中推断出这一切的。
准确地表达一下n(T),如下所示:
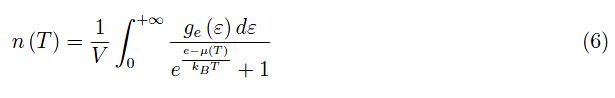
遵循理论物理学的标准方法,我们将物理变量(ε,µ)转换为无量纲变量(t,x),从而将问题无量纲化,定义如下:

经过简单的计算后:

其中:

是½阶费米-狄拉克积分,或更简单地说,费米-狄拉克积分(FDI)。等式(9)是以下的一个特例:
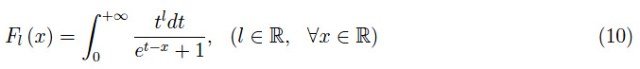
称为费米-狄拉克积分o forder l。
从方程(8)我们可以看出,FDI小于1.1量级的乘法因子,即电子浓度在量子浓度上的归一化,因此它是一个通用函数,可以描述任何纯半导体,无论电子的有效质量值是多少。请注意,FDI通过变量x与温度相关联,该变量在文献中通常用η表示(根据热能kBT归一化的化学势)。在经典极限−x≪1中,我们可以写:
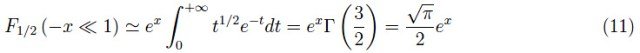
将电子浓度归一化为量子浓度,即通过变量r=n/nc,我们可以得到两种不同的表示方法:
温度域(T):
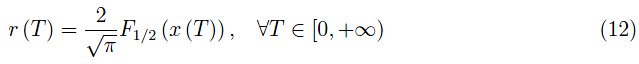
化学势域(x):
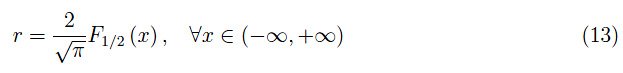
基于收敛准则,不难证明以下定理:
定理1:当l>-1时,l阶费米-狄拉克积分收敛。
对于l<–1,被积分的函数虽然不可求和,但仍然可以积分,因为它在积分域中符号恒定。
费米-狄拉克积分可以简化为:
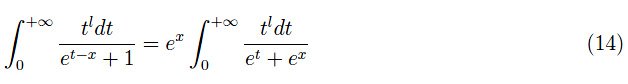
当然,即使是二元积分也不是简单可表达的。不过,让我们研究一下x的极值行为。当l>1时,积分均匀收敛,因此我们可以在积分符号下进行极限的操作:
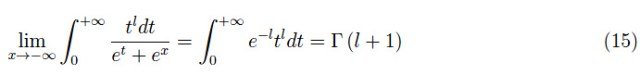
其中,Γ是欧拉伽马函数。所以,我们有:

因此,渐近行为:

这就是方程(11)的经典极限的推广。存在以下表示:
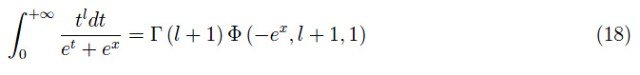
其中Φ是Lerch超越函数。这是一个复变量(w)的函数,参数取决于复数s和正整数a。对于费米-狄拉克积分,我们有:
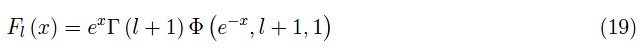
上述函数均在Mathematica中,因此积分Fl(x)在此环境下很容易计算,无需采用复杂的数值方法。在图1中,我们以对数报告了其中一些积分的趋势。Lerch函数还包含其他有趣的信息。
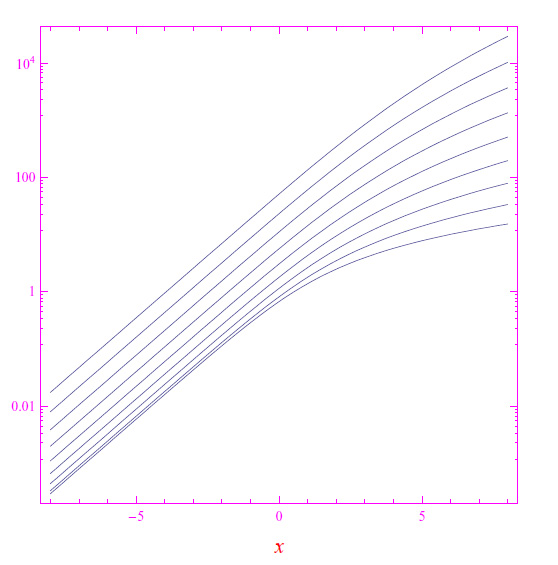
图1:从l=1/2开始,随着l增加,Fl(x)的一些积分
l=1/2时的方程(19)得出以下结果:
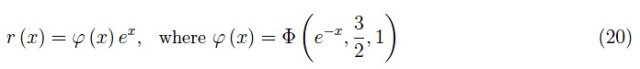
将ϕ(x)绘制在图2中。因此我们可以写:
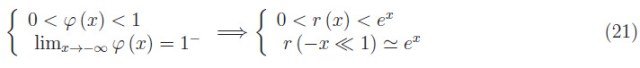
第一个不等式意味着半导体(或任何情况下的金属)导带中的电子浓度受到化学势x指数的限制,但不会呈指数增长。第二个不等式告诉我们,与金属不同,在半导体中,电子浓度随着化学势呈指数增长。
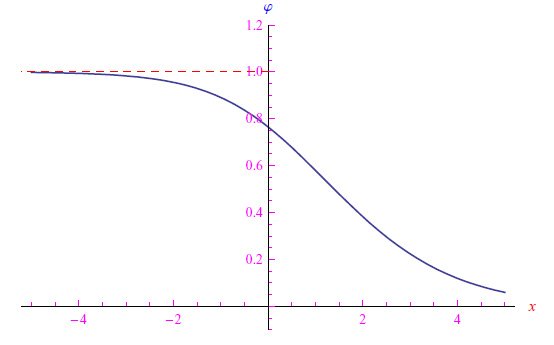
图2:函数ϕ(x)的图形,它是带有参数ex且参数l=1/2,a=1的LTF函数
对于上述情况,在量子浓度上归一化的电子浓度的精确表达式由式(13)给出,在经典极限中,该表达式由玻尔兹曼分布r=ex近似,其中的符号意义显而易见:

1977年,Joyce(焦易斯)和Dixon(帝克耸)用r的幂级数计算出了精确值x和近似值xBoltz之间的差值:
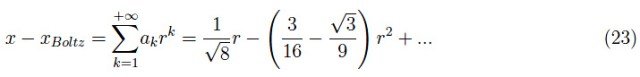
该级数迅速收敛,因此在最小非零阶下,我们有:

然后,通过Mathematica内置的兰伯特函数的推广对(24)求逆后,我们就可以以对数尺度绘制玻尔兹曼分布和与最小非零阶的焦易斯-帝克耸近似相比的准确趋势(图3)。
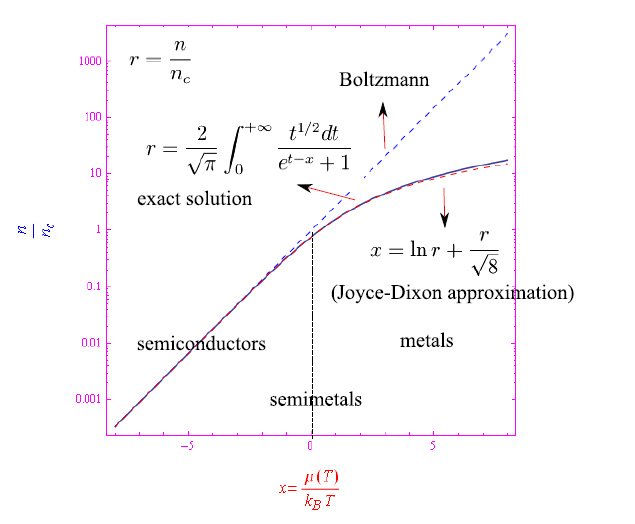
图3:半导体、金属和半金属之间的区别
通过对费米-狄拉克积分特性的介绍,我们可以对更现实的情况进行有趣的概括研究,例如:
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: The Fermi-Dirac integral and the Joyce-Dixon approximation,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯