
通过适当掺杂石墨烯样品,可以提高传导电子的费米温度,从而仿真金属的导电性。
正如之前文章所述,对半导体/半金属/金属区别的研究可以在两种不同的“环境”中进行。第一个(温度域)涉及化学势µ与绝对温度T的函数关系的数值确定。在第二个(化学势域)中,变量T被纳入一个无量纲量x,在−∞a+∞之间自由变化(这是费米子化学势的变化范围)。在这个模式下,由于x=0,半金属呈现为半导体和金属之间的界面,之前文章中生成了对数比例图,我们在图1中再次拿出了这张图。
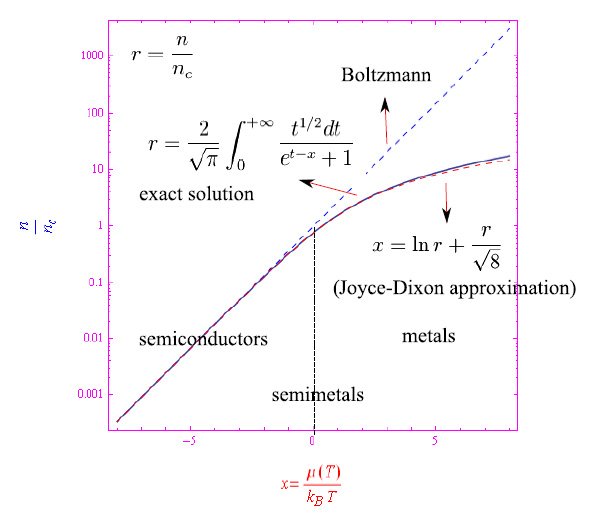
图1:半导体、金属和半金属之间的区别。纵坐标为归一化为量子浓度nc的电子浓度
作为一种半金属,石墨烯的禁带宽度为零,因此,无论温度T为多少,电子都存在于导带中。通过这种方式,它们仿真了金属的行为。然而,由于涉及电子和空穴(双极机制),石墨烯与金属的导电机制不同。由此可见,如果我们想最好地仿真金属的行为,我们必须对石墨烯进行适当的掺杂,以制造出一种导电性主要来自电子的器件。因此最终的结果是一个n型石墨烯的样品。
我们要提醒的是,在禁带宽度为εg的半导体中掺杂供体原子的效果在于生成以−εd为中心的极其密集的能谱,如图2所示,为了便于绘图,我们在图中画出了单个能级。
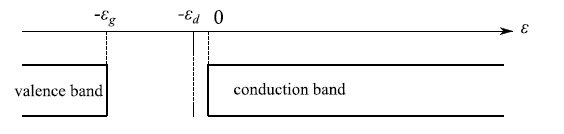
图2:−εd是供体原子的价电子的能级。事实上,我们有一个极其密集的能谱,其中各个能级最多由两个具有反平行自旋的电子组成
−εd与导带能级的极端接近有利于相应电子跃迁到导带。
如果像石墨烯那样εg=0会发生什么?答案非常简单:多余的电子(其电荷由相关的电离原子补偿)被“添加”到导带中已经存在的电子中。这样,通过适当密度的掺杂原子,就有可能实现与金属相同量级的电子浓度。
导带中电子浓度的增加对应于费米能εF的增加。事实上,我们已经知道:

我们可以看到,εF与n2/3成正比,其中n=Ne/V,V是样品的体积。对于杂质浓度为n=4·1021cm-3的给定石墨烯样品,从等式(1)我们得到ε=4.6 eV,因此费米温度T=53378.7K(我们假设石墨烯中电子的有效质量m∗e=0.2me)。
由此可见,在室温下,电子气具有很强的简并。在图3中,我们假设µ(T)=εF,展示了不同温度下相应Fermi-Dirac分布函数(费米-狄拉克分布函数)的趋势。我们考虑的温度T≪TF,此时化学势与εF=µ(0)略有不同,因此最后一个假设是合理的。
为了获得更细致的趋势,需要求解索末菲函数方程。这个新表达式引用了µ(T)中的函数方程,对于T≪TF有效,它源于著名的费米-狄拉克积分的索末菲展开式,以物理单位而非无量纲单位表示。结果如下:
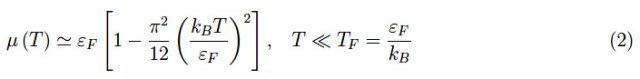
从图4的相应图中我们可以看到,在T≪TF范围内,它与费米能的偏差可以忽略不计。
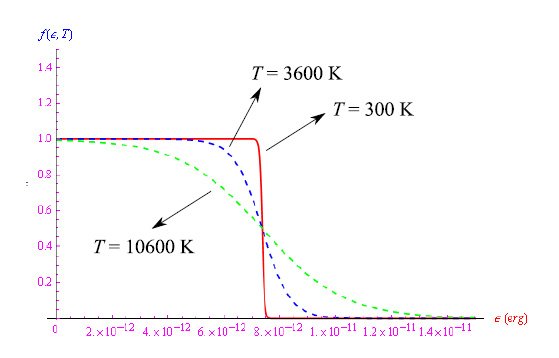
图3:用Mathematica仿真以电子浓度为4·1021cm-3的方式掺杂的石墨烯的电子的费米-狄拉克分布函数的趋势。费米温度的高值意味着即使在室温下也有很强的简并性
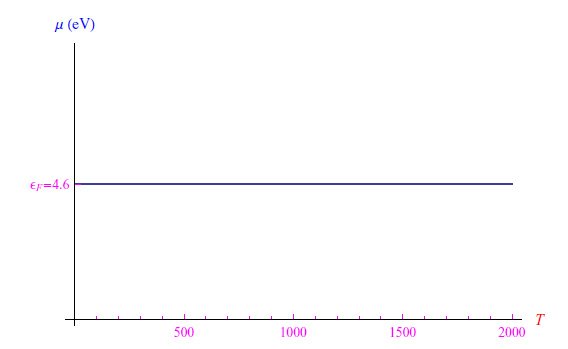
图4:式(2)表示的化学势趋势
将式(2)代入费米-狄拉克分布函数表达式,可得:
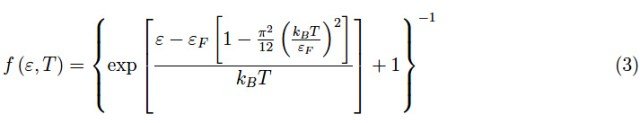
由此可见,函数向零的“跳跃”并非发生在εF处,而是发生在一个稍有不同的值处,正如我们从图5中看到的那样。请注意,温度3600、10600K是理论温度,实验中还无法达到。
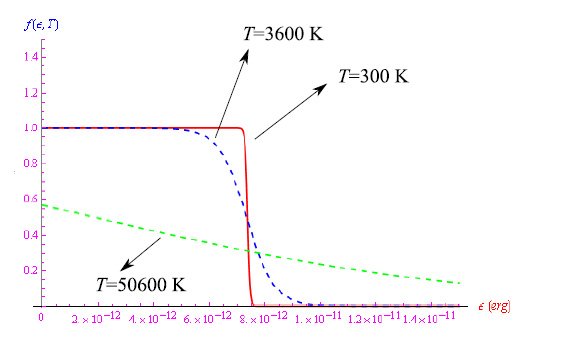
图5:与图3中相同石墨烯样品相关的分布函数(3)的趋势
因此,化学势是半导体/半金属/金属分类中的一个基本物理量。更准确地说,正是它对温度的依赖性决定了被归类为“固态”的物质聚集状态的行为。就n型石墨烯的具体情况而言,从本期进行的论证可以推断出,其导电性与符号σ=enµe的含义相同。由于n不会随温度发生明显变化,因此其行为与金属类似。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: the Fermi temperature of electrons in doped graphene,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯