
如果我们想要对某些模拟波形进行采样(sampling),就像以某种特定的转换率进行模数转换一样,进行这一转换的速率存在一个相对于模拟信号最高频率分量的绝对下限。为了让采样过程产生有效的结果,就不能违反这一限制。我们可不希望信号出现“混叠”(aliasing )现象。
我们在这里使用的“混叠”一词,与间谍惊悚小说或犯罪小说毫无关系。混叠是指当以高于采样频率倒数一半的规律时间间隔,针对某些模拟波形的瞬态值进行采样时,就可能发生这种不必要的效应。如果我们以每微秒对某些波形采样一次,那么采样间隔就是1微秒的一半,采样频率限制为2MHz或更快。
如果采样波形的频率成分分量大于采样频率的50%,就会出现混叠。反过来说,如果采样频率过低,也会产生混叠现象。任何采样速率一旦低于被采样波形最高频率分量的两倍,就会产生混叠效应。
接下来的问题是:为什么?
美国喜剧演员“教授”Irwin Corey曾经提出过一个类似的问题:“为什么天空是蓝色的?”他的答案是这样的:“这个问题必须分为两个部分。第一部分是'为什么?,这是人类从古至今一直在问的问题。为什么呢?我也不知道。第二部分是'天空是蓝色的吗?'答案是'没错!”
幸运的是,我们可以用更好的方式来说明,具体如下文介绍。
采样过程可以看作是将被采样的波形乘以一个工作周期很窄的脉冲波形,该波形在大部分时间为零值,而在很窄的采样时间间隔内具有单位值。该采样波形将含有丰富的谐波。采样频率本身会有一条频谱线,采样频率的每个谐波也都会有频谱线。如图1所示,每条频谱线都会有边带(sideband),从这些采样频率频谱线向上和向下延伸,以便与采样波形的带宽保持一致。
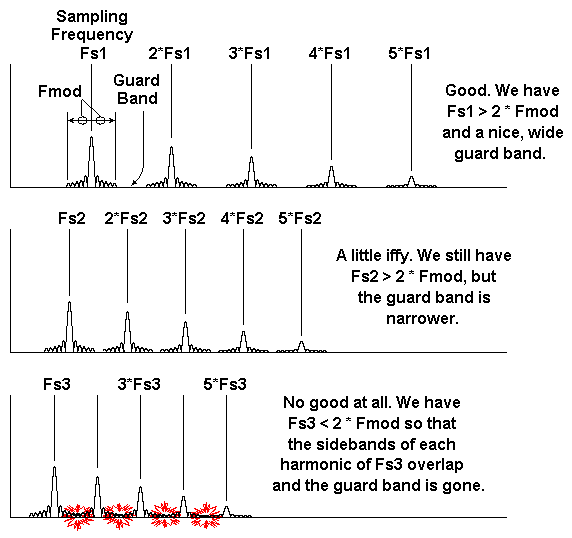
图1:采样与混叠时,每条频谱线都会有边带并从这些取样频率频谱线向上和向下延伸,与采样波形的带宽保持一致。
在采样波形时,由已采样后的波形进行振幅调制,因此我将这些已采样波形的最高频率分量称为Fmod。每个带宽为2 * Fmod。
如果采样频率足够高(如Fs1),图示的边带就不会重叠。在它们之间存在着一个适当的保护带,因而不会出现混叠现象。
如果采样频率开始降低(如Fs2),边带就会开始靠拢,出现看起来不是那么“舒适”(不确定这一词是否贴切)的保护带。
如果采样频率过低(如Fs3小于Fmod的两倍),边带就会重叠并因此出现混叠。这也导致采样失去其完整性。所采样到的波形也就无法从这个系统的欠采样输出中重建。
让我们向Claude Shannon(1916年4月30日—2001年2月24日)及其采样理论致敬。
(原文刊登于EDN美国版,参考链接:Sampling and aliasing,由Susan Hong编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯