
振荡器,亦称为非稳定多谐振荡器,是产生周期性信号的电子部件。其应用非常广泛,如用于时钟、示波器、乐器以及各种自动化系统等等。就振荡器的实现而言,最有趣的一种方法是利用集成电路中的逻辑门,这样就可以很容易地实现具有特定频率和信号幅度的数字振荡器。
方波是由数字振荡器产生的最常见的信号类型之一,利用最简单的振荡器即可生成。进一步,只要采取适当的设计技术与技巧,也可以产生正弦波和三角波。这些电路的工作原理,实际上都是利用特定的电压阈值,来控制逻辑状态的转换。
利用施密特触发器的反相器(NOT),就可以设计一个简单的方波发生器,具体如图1所示。之所以采用这种解决方案,是因为触发器的逻辑不确定性区域要窄得多,并且逻辑门可以敏锐地执行其切换。简单电路组成如下:
如果要求频率可变,可以用电位计或可调电阻器来代替固定电阻器。振荡器的工作原理,可以通过观察NOT门的两种可能逻辑状态来理解,具体如下:
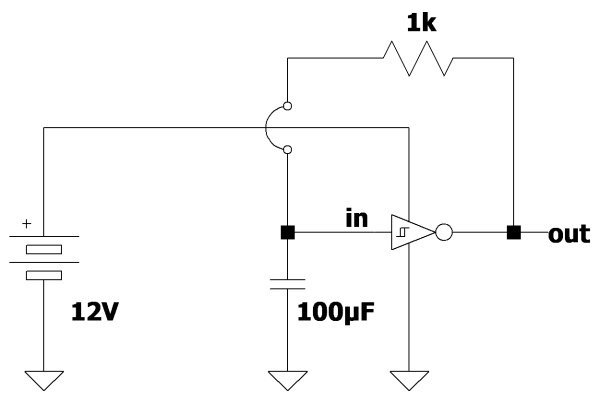
图1:基本型NOT门振荡器的设计原理图。
接下来,观察一下NOT端口的各端子上,以及触发反相器的IN和OUT引脚上都发生了什么,这通过观察图2中的波形图更容易理解。该电路的电源电压为12V(Vcc)。反相器输入信号为红色迹线(Vin),而输出信号为蓝色迹线(Vout)。值得注意的是,输入信号从未达到0V或Vcc;相反,它停留在较窄的范围内并呈现锯齿波形。这些电位决定了反相器的开关间隔,根据所用集成电路的固有特性,在输出端,发现输出信号“几乎”为方波,幅度在(GND+n1)伏与(VCC-n2)伏之间变化。当采用上述元器件时,所产生的信号频率大约为14Hz。
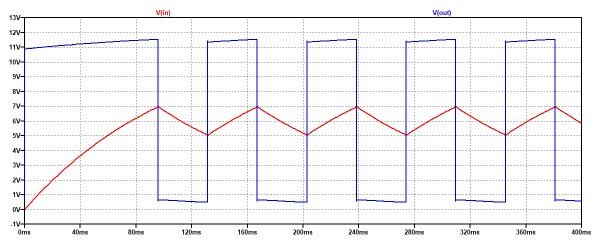
图2:触发NOT门的输入和输出电压。
理论上讲,此时的输出信号已经可以利用,但再添加一个NOT门,就可显著改善其方波性能。从图3中可以看出,由于没有采用模拟元件,因此额外增加了一级反相器,从而可以提高输出信号的质量。另外,由于信号的相位被反转,可再采用一级反相器,使输出信号相位与原始信号相同即可。通过分析波形图,发现电路包含如下三个输出:
·out1
为第一个反相器的输出信号,由于电阻器和电容器的存在,它可以被认为是数字和模拟的混合。
·out2
为数字输出,其相位与out1相反。
·out3
从各个方面来看,这也是一个数字输出,并与out1同相。与out1相比,其方波质量要好得多,并且分别非常接近GND(对应于低逻辑电平)和VCC(对应于高逻辑电平)。
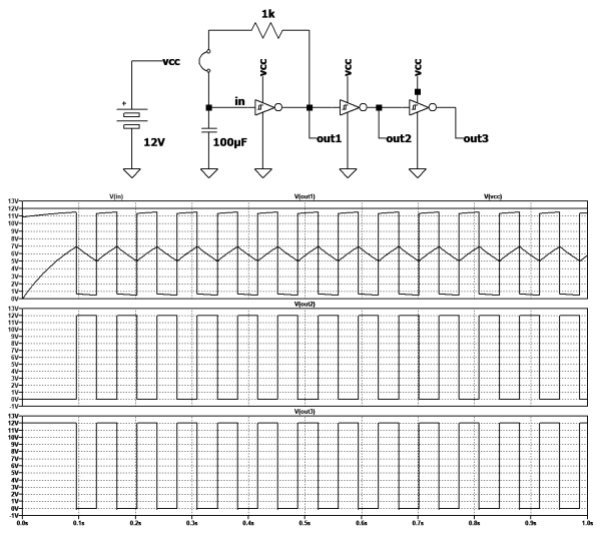
图3:第二级反相器改善了输出信号质量,但使信号反相;第三级反相器使其与输入同相。
不过,利用含逻辑门的集成电路只能处理小电流,并且每个引脚的输出值都不能高于器件数据表中的额定值。此时,为了提高电流,可以将多个输出并联连接,如图4所示。另外还建议采用二极管来避免输出信号受干扰。每个二极管都应确保尽可能低的势垒,因此最好采用肖特基型二极管。这类方案可以按如下方式采用六个反相器:
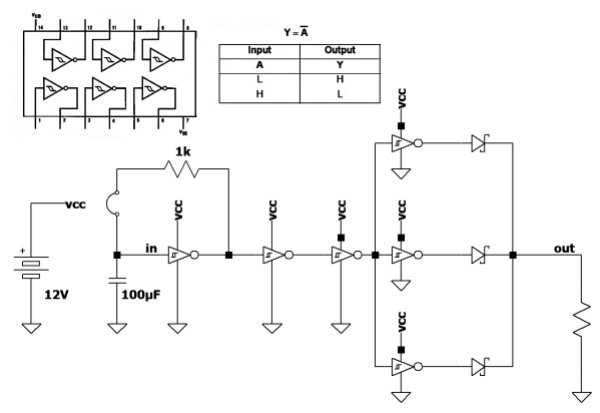
图4:通过并联多个输出来提高输出电流。
输出信号的频率很大程度上取决于所采用的电阻器和电容器构成的时常数。一般地,计算振荡频率的公式为:
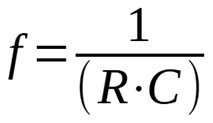
不过,由上述公式计算得出的频率仅为一个近似值,因为还与其他因素有关,包括温度、所用集成电路类型、端口类型、电源电压和其他次生参数等。即便官方数据表规定了标准值,但不同制造商生产的同一型号集成电路,通常还都可能会有差异。如上所述,在1k欧姆电阻器和100uF电解电容器的情况下,所产生的信号频率大约为14Hz。对于低频周期性信号的产生而言,设计中并没有什么特别限制。不过,当频率开始大幅上升(比如kHz的数量级)时,就必须考虑影响所生成信号质量的许多方面。广义而言,包括:
在设计逻辑门振荡器时,必须记住,实际频率可能与公式计算的理论频率有很大不同。因此,对于给定的振荡频率,在理论上粗略地计算所采用的无源元件值之后,实际中有必要对电阻器和电容器的值进行调整。
在上面讨论的方案中,涉及到的占空比均为50%的对称方波。这意味着生成的信号在半个周期内处于导通状态,在接下来的半个周期中处于截止状态,以此类推。而现实中,通常需要具有不同占空比的信号,即接通状态比断开状态持续更长或更短的信号。此时,可以采用图5所示的电路。该电路采用两只反相连接的二极管。两只电阻器的值决定了两个不同的接通和断开时刻。任何类型的二极管都可用来实现各种不同的占空比。一般来说,利用图5中二极管的电阻器值之间的关系如下:
通过采用尽可能多的电位计或可调电阻器来替换固定电阻器,即可方便地调整电阻器值,来生成具有可变占空比的周期性信号。
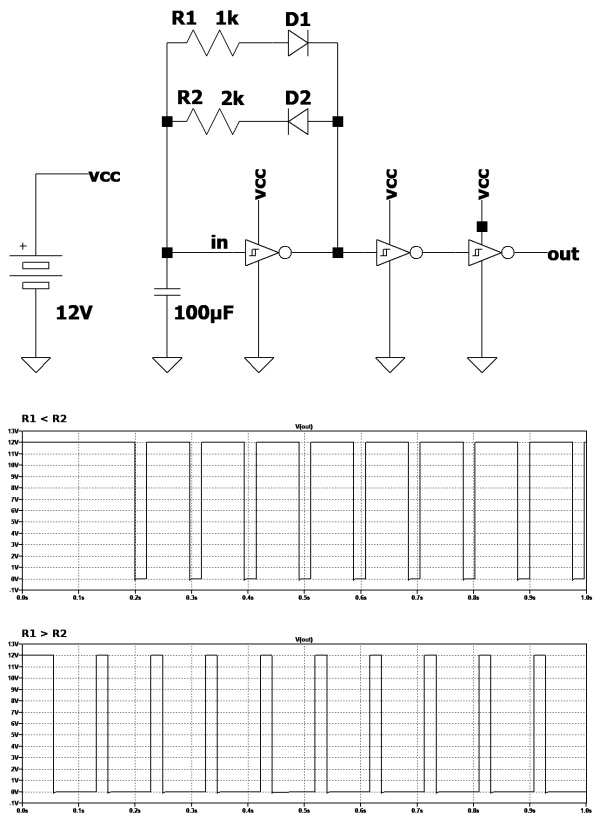
图5:由于R1/D1和R2/D2的采用,能够改变占空比并使HIGH和LOW信号不对称。
逻辑门振荡器是利用逻辑门产生周期性信号的电子部件。方案相对容易实现,并且可以主要用来生成方波。此外,所用组件的成本效益有助于使其成为一种实用且有效的解决方案。这些类型的振荡器通常非常稳健和可靠,并且主要功能几乎不会受到严重影响。缺点是无法直接生成复杂波形,所幸依赖模拟电路或微控制器可以实现。除了利用NOT门实现的基本型电路外,在比较复杂的电路中,解决方案中还会利用其他逻辑门,并将各种逻辑门进行适当组合。
(原文刊登于EDN姊妹网站EEWeb,参考链接:Digital Electronics Course – Part 11: Oscillators with Logic Gates,由Jan编译。)
本文转自《电子工程专辑》2024年3月刊杂志文章,版权所有,禁止转载。点击申请免费杂志订阅
 最前沿的电子设计资讯
最前沿的电子设计资讯