
Stan Wagon在他的著作中提出了一个Mathematica例程,用于消除在绘制数值不稳定函数图形时的舍入误差。但在数值求解确定p型半导体中电子化学势的函数方程时,我们遇到了一个更为复杂的舍入问题。
为了快速回顾之前文章中提出的论点,让我们重写一下逸度z(T)的函数方程:
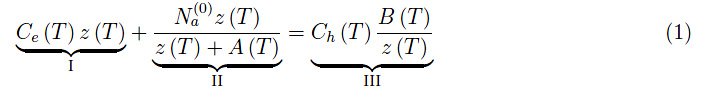
其中I=导带中的电子数,II=以−εa为中心的禁带能级中的电子数,III=价带中的空穴数。然后我们定义了无量纲量:
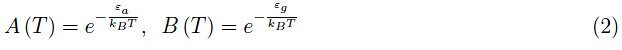
在低温范围内,I项可以忽略不计。从物理上讲,这意味着当T≪300K时,逸度z(T)接近于零。因此,在低温极限下,方程(1)的解表现得类似于以下方程的解:
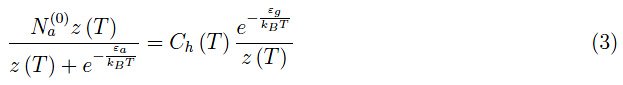
这是z(T)的二次方程式。计算完成后(丢弃负根,因为必须要z(T)>0):
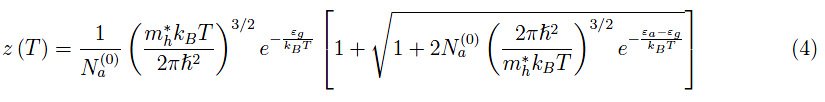
化学势由下式给出:
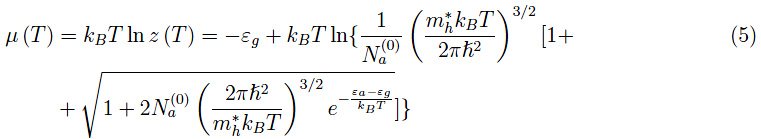
为了确定T→0的极限,我们利用以下命题(证明就留给读者吧):
命题1
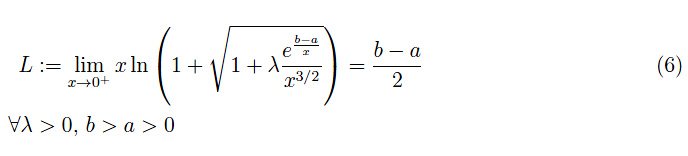
其中:
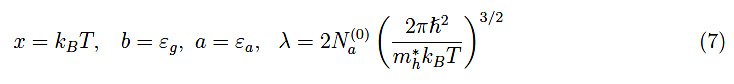
等式(6)涉及:

即费米能级。(6)式有一个显著的物理解释,因为其值与正参数λ无关,因此也与三价杂质的总数Na(0)无关。我们发现,对于任何Na(0)>0,费米能级位于价带顶部与Na(0)产生的能级−εa的中间。在图1中,显示了指定Na(0)时函数(5)的趋势,从中我们可以看出,当0<T<100K时,化学势近似为μ0(方程(8))。
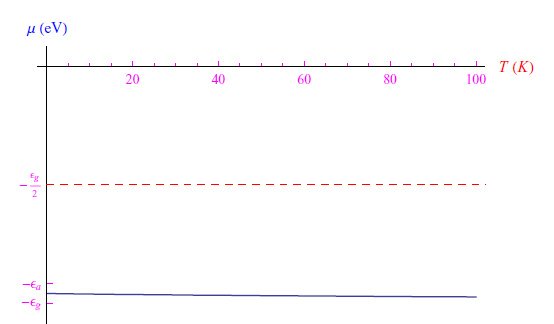
图1:低温极限化学势趋势
命题2

证明。证明方式与命题1类似。使用Mathematica类型的计算环境,证明当T→0时,逸度z(T)是无穷大阶的无穷小量,这与之前文章中证明的推论一致。
这里必须求解方程(1),该方程显然是z(T)的三次方程。通过在Mathematica计算环境中编写适当的程序,我们发现Na(0)=102cm−3的图形趋势如图2所示,其中存在明显的舍入问题。通过缩小热范围并将其与在低温极限下找到的解(5)进行比较,我们得到了图3中的图形。通过MaxRecursion指令可以减少振荡次数,如图4所示。
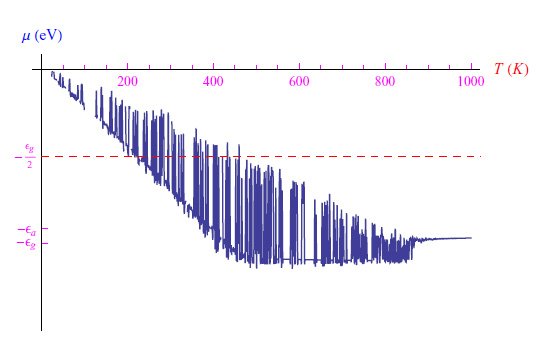
图2:Na(0)=100的化学势趋势
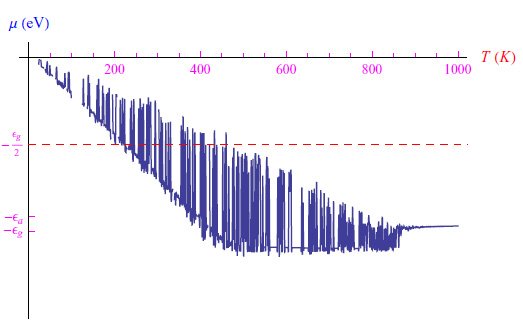
图3:红色曲线是解(5)在低温下的图形,它试图将每个温度下的解决方案进行匹配,但徒劳无功
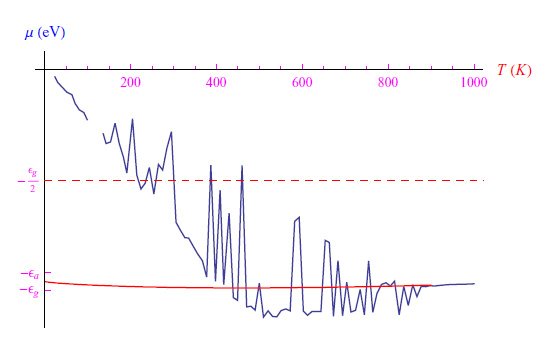
图4:与图3相同的图,不同之处在于我们使用MaxRecursion指令减少了振荡次数
从执行的图形分析中,我们推断出,对于Mathematica内核,当热力学平衡温度趋于零时,化学势趋于零。但据我们所知,这是一个错误,因为只有当禁带εg为零时才会出现这种情况。否则,化学势将位于−εg和−εa之间。误导Mathematica的是,在T→0的极限下,逸度z(T)是无穷大阶的无穷小量。简而言之,在T=0的右邻域中,Mathematica计算出这个量的指数小值,这就产生了如图5所示的不规则趋势。
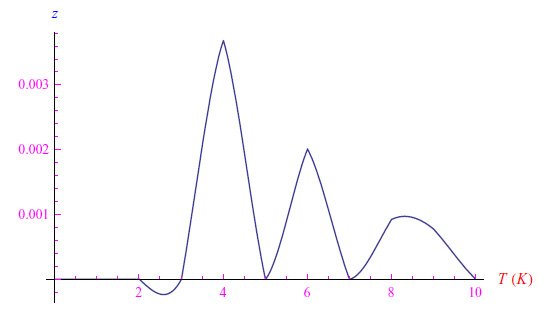
图5:低温下的逸度z(T)趋势
我们进行了数学分析,从温度T到热能x=kBT,或者说,从能量单位(eV)到温度。以下是我们的结论:
舍入是由Na(0)>0产生的。显然,对于N(0)=0,我们就陷入了µ(T)的直接计算的固有情况。否则,掺杂(Na(0)>0)会破坏以封闭形式求解函数方程(1)的可能性。这样,数值解就无法基本表达了。
代换T→x=kBT压缩了自变量的尺度,抑制了振荡。然而,Mathematica内核仍然返回错误的结果µ(0)=0,如图(6)所示。
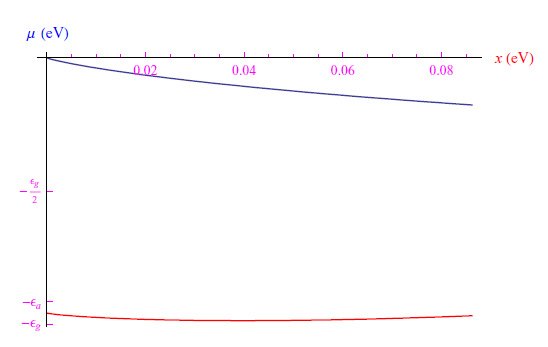
图6:随着变量T→x=kBT的变化,振荡消失,但对于Mathematica内核,化学势在T→0时的极限为零
最后,我们在图7中展示了三种情况下化学势的变化趋势:1)掺杂三价杂质(p型);2)掺杂五价杂质(n型);3)纯半导体。
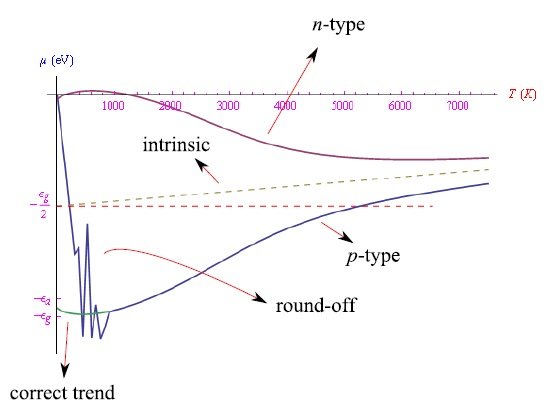
图7:三种可能情况下的化学势趋势(温度值为指示值)。随着温度无限升高,两条曲线逐渐趋向于定义未掺杂半导体化学势的直线
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: chemical potential and difficult plots,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯