
本文中我们完成了从之前文章中开始的分析,使用Mathematica仿真了硅(Si)样品中铝(Al)原子的掺杂。由于工作量很大,我们将文章分为两部分。在这里,我们将研究电子自旋在三价杂质掺杂中的作用。
通过一系列问答,我们深入研究了铝等三价杂质的掺杂机制。图1举例说明了这一过程,打破共价键需要一定量的能量(热能)。为了不失一般性,我们以单位体积的Si样品为例。
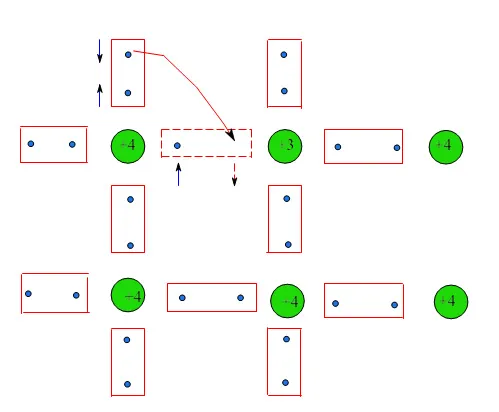
图1:顶部的小红色矩形,其中指定了电子的自旋状态(蓝色箭头),在热扰动后会发生断裂。因此,电子被释放,它没有获得属于导带的能量,而是完成了Si的一个价电子的自旋单重态,该价电子试图与三价杂质的缺失电子结合
问题:什么共价键断裂产生的电子会“填充”杂质空位,而不是进入导带(如没有杂质时发生的情况那样)?
答:对于每个三价杂质,相邻的Si原子中都存在一个未配对的电子,因此来自断裂共价键的电子倾向于与该电子一起完成自旋单量子态(图1),留下一个空穴,而该空穴又可以由来自另一个断裂共价键的电子填充。通过添加大量杂质,可以重复此过程。结果就是形成同样数量的宏观空穴,因此在施加电场后,对电导率的主要贡献来自空穴(p型半导体)。
如图2所示,获得一个电子的单个三价杂质变成了负离子。与剩余的三个电子相比,多余的电子与离子的结合程度较低,因此其占据的能级略高于价带的顶部。大量三价杂质的存在会产生以−εa=−εg+∆为中心的极其密集的能谱,其中εg>0为禁带,而0<∆≪εg。根据泡利不相容原理,每个能级最多由两个具有反向平行自旋的电子占据。
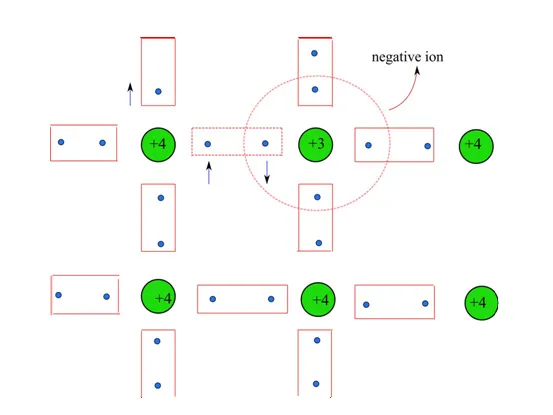
图2:共价键断裂后获得电子,形成负离子
让我们回顾一下前面数字的符号:Ne(T)和Nh(T)分别是半导体在温度T下处于热力学平衡时导带中的电子数和价带中的空穴数。总电荷Q(T)表示为负电荷与正电荷之和:
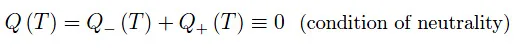
和往常一样,如果e是电子电荷的绝对值,则我们有:
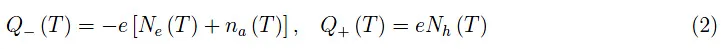
其中na(T)是负离子受体的数量。将(2)代入(1)中,可得:
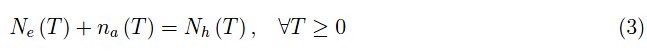
下图总结了可能出现的情况,很有启发性:

如在前面的教程中看到的那样,在这三种情况下,Ne(T)、Nh(T)的量由下式给出:
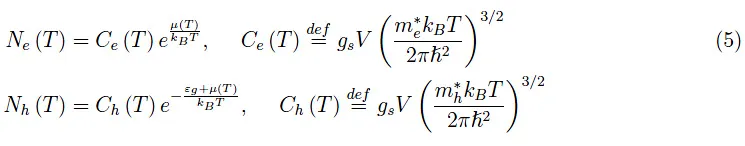
如上所述,掺杂三价杂质会产生以−εa为中心的非常密集的能谱,如图3所示。高能谱密度使我们能够应用连续能谱近似:
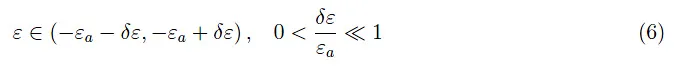
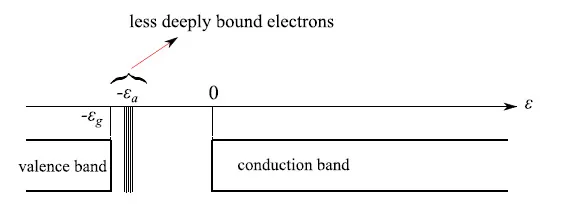
图3:禁带中的每个能级最多被两个具有反向平行自旋的电子占据
按照(4),我们在图4中展示了可能的情况,其中红色矩形表示连续谱近似。
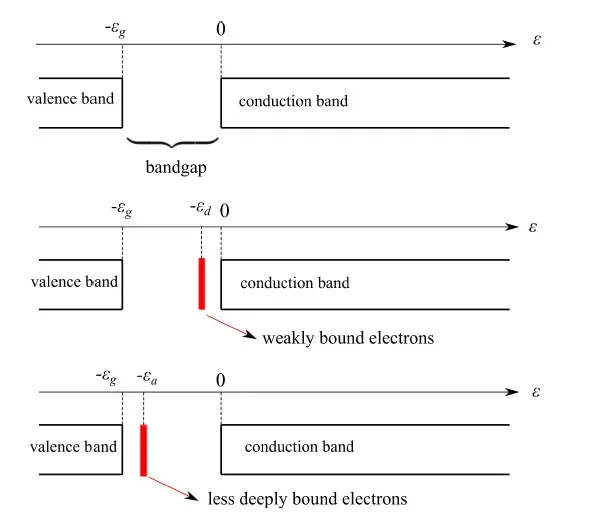
图4:三种情况下能级的图形表示:1)本征型;2)n型;3)p型
在明确了这一点之后,电子通过能级(6)产生的空穴总数等于三价杂质的总数。设这个数字为Na(0)。在温度T>0时,电离的受体原子数由下式给出:

其中Na(T)是尚未电离的受体原子数。假设已知Na(0),我们需要确定Na(T)。在进行此计算之前,让我们先研究一下方程(3)的物理内容,我们可以将其重写如下:
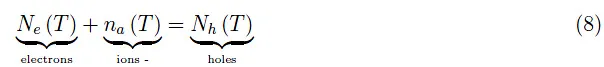
在绝对零度时,热能为零:共价键不会断裂,并且由于各个量为零,方程(8)简化为恒等式0=0。随着温度升高,共价键开始断裂,但如前所述,释放的电子不会进入导带,而是占据受体能级(在−εa附近)。由于泡利不相容原理(每个能级最多由两个具有反向平行自旋的电子占据),这样的过程无法无限期地持续下去。因此,当温度达到所有受体能级都被占据的程度时,从共价键中释放出来的相应电子将被迫占据导带中的能级,众所周知,这就构成了连续能谱。为了更加定量,对于温度T>0但不太高的情况,方程(8)变为:

因为热能刚好足以将电子推到−εa附近的能级。因此,在这个温度范围内,Ne(T)=0。在适当的温度下,−εa中的电子可以进入导带,这个过程由完整的方程(8)控制。随着T无限增加:

由于在足够高的温度下,受体能级全部被占据,本征电导率被激活。现在让我们继续计算Na(T),进而计算na(T)(方程(7))。利用费米-狄拉克分布函数,我们可以确定单个杂质的电离概率:
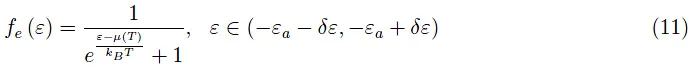
我们可以近似如下:
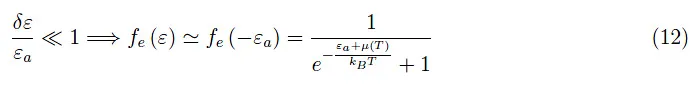
因此,我们有:
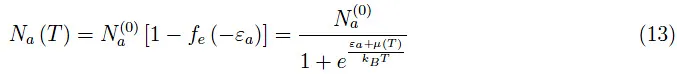
我们寻找的量是方程(7),现在对于方程(13)来说,它变成:

将各种量代入方程(8),我们得到:
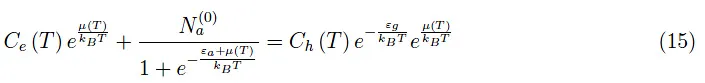
μ(T)中的超越方程可以通过转换为逸度z(T)=exp(μ(T)/kBT)来代数化:
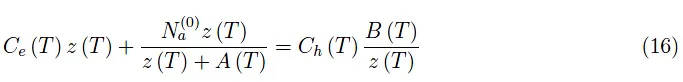
其中:
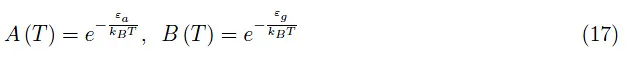
最后,我们强调了自旋单重态的形成所起的作用,它反映了泡利不相容原理,从而结束了这一部分分析,尽管它还具有丰富的物理内容。因此,我们面对的是典型的量子效应,而这些效应基本上超出了我们基于经典力学的认知范围。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: the “dance” of electronic spin in p-type semiconductors,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯