
基本负温度系数(NTC)热敏电阻的成本低、体积小、结构坚固、精度高、用途广、灵敏度高,因此成为最受欢迎的温度传感器之一也就不足为奇了。然而,它们的温度响应函数是高度非线性的(实际上是指数型的),这使得激励和信号数字化及处理成为了一项复杂的设计工作。
典型的NTC热敏电阻的数据表(例如,Molex 2152723605)用四个参数(公式1至5)概括了热电特性,如图1所示(数字借用自2152723605的数据):
To=额定/校准温度(25°C=298.15K) (1)
Ro=To时的电阻(10k±1%) (2)
b=beta(3892K) (3)
耗散(自热)系数(1.5mW/°C) (4)
然后,热敏电阻的电阻(Rt)与开尔文温度(T)的关系可通过以下方式预测:
Rt = Ro exp(b(T-1 – To-1)) (5)
应用经典的KISS原则,我们可以在图1中看到一个从热敏电阻中获取信号的最简单电路候选方案,并进行了一些基本的数学运算以从其输出和上面的参数1、2和3中筛选出温度测量值。
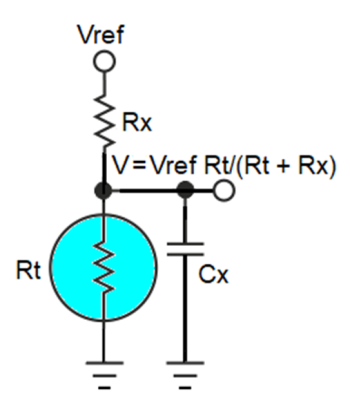
图1:基本热敏电阻无源激励电路:Cx=可选降噪电容,大约为100nF;Rx=激励电阻;Rt = Rx(V/Vref)/(1 – V/Vref);T = (Ln(Rt/Rx)/b + Tx-1)-1。
除了Cx和热敏电阻本身外,图1中唯一的组件是Rx。如何选择其最佳值?
直觉和数学都证实,最佳(至少接近最佳)选择是使Rx等于应用所需的温度测量范围中间的热敏电阻阻值。所述中点温度(称为Tx)将输出V=Vref/2,从而在测量范围内对称分配ADC分辨率。公式5告诉了我们如何实现这一点。
假设我们选择0℃至100℃的测量范围,则Tx=50℃=323.15K,公式5的算术结果告诉我们(使用2152723605的数字):
Rx = Ro exp(b(Tx-1 – To-1))
Rx = 10000 exp(3892(323.15-1 – 298.15-1))
Rx = 3643(最接近的标准1%值=3650)
现在,如果我们简单地选择Vref=5V作为Rx输入和ADC参考输入(因为这是一个比率测量,Vref的绝对值相对来说并不重要),我们可以设置:
X = ADC/2N = V/Vref
然后
T = (Ln(X/(1 – X))/b + Tx-1)-1
℃ = (Ln(X/(1 – X))/3892 + 0.003095)-1– 273.15
耗散(自热)系数(1.5mW/°C)怎么样?
我们显然不希望热敏电阻的自热严重干扰温度测量。自热误差的合理限度可能是半度,对于2152723803的1.5mW/°C来说,这将决定将最大耗散限制在不超过:
Pmax = (1.5 mW)/2 = 0.75 mW
当Rt=Rx时,耗散最大为Vref2/4/Rx,因此在这种情况下Vref=5V将是:
Pmax=Vref2/4/Rx=25/4/3650=1.7mW=1.1°C
这比规定的最大自热误差高出两倍多。该怎么办?不用担心,图2给出了解决方案。
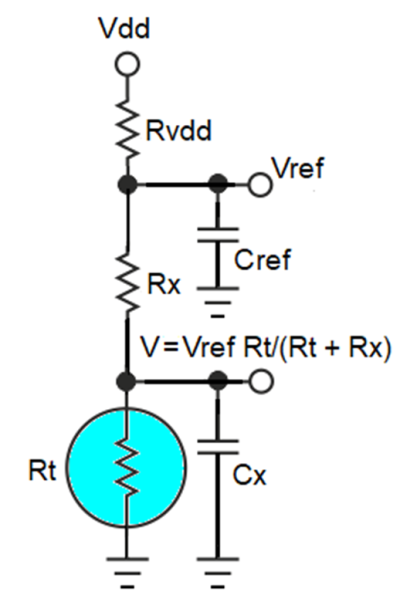
图2:Rvdd将热敏电阻的最大自热限制为Pmax:Pmax=Vdd2/4/(Rx+Rvdd);除非Rvdd=Vdd2/4/Pmax–Rx>0,否则Rvdd=0;(Vdd Rx/(Rvdd+Rx))<Vref<Vdd。
再次代入2152723605的数字并保持Vdd=5V:
Rvdd = 25/4/(0.75 mW) – 3650
Rvdd = 8333 – 3650 = 4.7k
Pmax = 0.749 mW
2.8 V < Vref < 5 V
请注意,如果图2的数学运算得出Rvdd的值为零或负值,则不需要Rvdd,并且原始图1的电路也能正常工作。
尽管Vref会随Rt和温度而变化,但外部参考单片式ADC通常对所示范围内的Vref变化具有很强的容差性,并且可以执行准确的比例转换。
(原文刊登于EDN美国版,参考链接:Getting positive results from NTC thermistors with a simple passive interface,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯