
在之前的文章中,我们通过添加磷原子在软件中重建了硅样品的掺杂。在本文中,我们将研究一种可以在Mathematica/Maxima/Maple类型的CAS(计算机代数系统)上实现的算法。与传统的仿真软件相比,我们的方法为用户开发合适的数学模型提供了可能性。
化学势µ(T)(俗称费米能级)是一张“万能牌”,它使我们能够确定任何半导体(掺杂的或纯的)中电子和空穴的浓度。为此,我们可以用一个被称为逸度的新量来重新表述与费米气体相关的主要结果。
在热力学中,化学势是一个强度量,它表征粒子数可变的系统的平衡状态。在量子统计力学中,这个量在玻色子和费米子的分布函数中起着决定性的作用。特别是,后者由前面的文章中已经提到的费米-狄拉克分布函数描述:
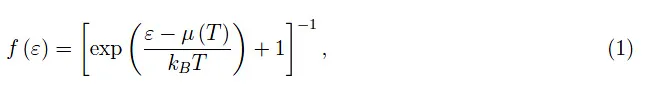
其中化学势可以从−∞到+∞变化。
在之前的文章中,我们通过无量纲量定义了式(1)所描述的粒子气体的逸度:

定义z(T)的指数参数是归一化为热能kBT的化学势。高逸度值意味着上述主题的值较高,因此化学势也较高。逸度一词源于这一事实,粒子倾向于从化学势较高的区域迁移到化学势较低的区域。因此,在z(T)值较高时,预计会出现明显的粒子迁移。
我们可以用z(T)来表示方程(1):
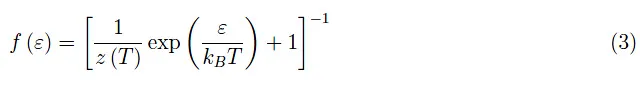
因此,我们有:
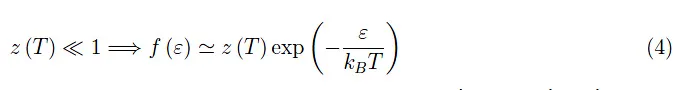
这就是玻尔兹曼分布(经典统计力学)。事实上,在之前的文章中,我们已将z(T)定义为简并参数(A(T)):对于z(T)的不可忽略值,存在 “简并”,即偏离经典行为。这是合理的,因为如上所述,较高的z(T)值对应于明显的粒子迁移,在z(T)取较低值的区域,粒子会趋于变浓。但这相当于增加了粒子的浓度,从而增加了费米温度TF和简并的可能性(当温度T≪TF时),正如之前的研究中确定的那样。
由于µ(T)是一个物理量,我们期望该函数在[0,+∞)中具有连续性,并且具有一阶导数。定理如下,其证明是直接的:
定理1:
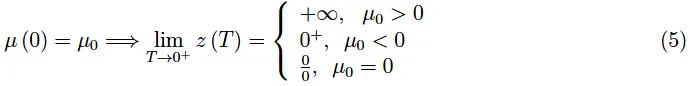
我们注意到µ0>0的情况是费米气体的情况,众所周知,它在温度T=0时完全简并。顺便说一句,T=0时的逸度是无限的。这证实了之前关于逸度含义的论证,因为它与偏离经典行为有关。从数学上讲,我们看到,与µ(T)不同,函数z(T)在T→0时会出现奇点。
下面的推论同样可以直接得到证明:
推论2:如果µ(0)<0,则T→0+的逸度是无穷大阶的无穷小。如果µ(0)>0,则T→0+的逸度是无穷大阶的无穷大。推论(2)的第一部分适用于半导体的情况,因为µ(0)<0。对于石墨烯等半金属,由于禁带为零,所以µ(0)=0。因此,根据定理1,对于T→0,逸度是不确定的。
图1总结了可能的情况。
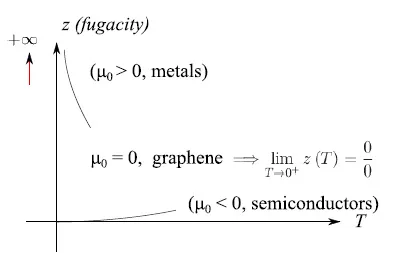
图1:与在[0,+∞)中连续的函数µ(T)不同,逸度在绝对零度处可能存在奇点(金属)
在之前的文章中,我们用Ne(T)、Nh(T)表示导带中的电子总数,以及价带中的空穴总数。由于我们的计算实验涉及单位体积(1cm3)的硅样品,因此预测的量是电子/空穴数量的密度,更简单地说就是浓度。观察到这些量通常用n、p表示,我们有:
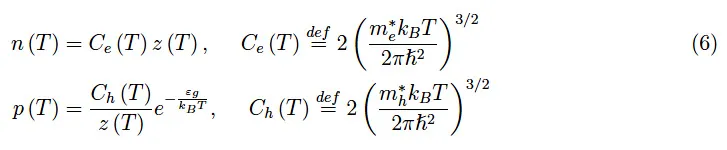
在开发算法之前,应该注意,刚刚写的公式在T=0时会产生问题。在上一节中,我们看到,对于T→0+,逸度z(T)是无穷大阶的无穷小。因此,在方程(6)的第二个式子中执行此极限将返回不定形式0·∞,这在数值计算程序中会转换为错误。因此,我们需要确定一个温度范围,其初始温度接近零,但永远不会正好为零。
浓度n(T)和p(T)由一个函数方程关联,该方程保证了半导体的电中性(在没有外部电场的情况下)。考虑到掺杂五价/四价杂质,上述方程变为:

其中符号(+)表示下标d(五价杂质),之前已经讨论过这种情况;符号(-)表示下标a(三价杂质),我们将在后续文章中讨论。(7)是未知函数z(T)的一个方程,求解该方程后,我们可以计算出浓度n(T)、p(T),从而计算出电导率:
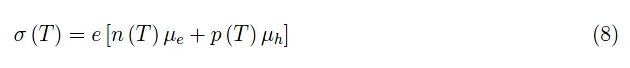
我们已经解释了除电子和空穴的迁移率µe、µh之外的各种量的温度相关性(在后续文章中,我们将详细研究最后两个量及其与温度的关系)。计算方案如图2所示。
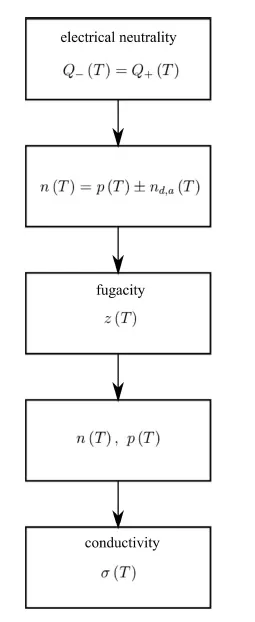
图2:确定掺杂半导体电导率的计算方案
测量单位是困扰这一话题讨论的一个问题。在单位制中,迁移率以cm2V−1s−1为单位;对于硅,µe=1600 cm2V−1s−1,µh=400 cm2V−1s−1。电子电荷的绝对值为e=1.60217733×10−19C。
然后,计算方案2将被转换为所用CAS的相应语法。例如,使用Mathematica,我们可以得到以下结果:
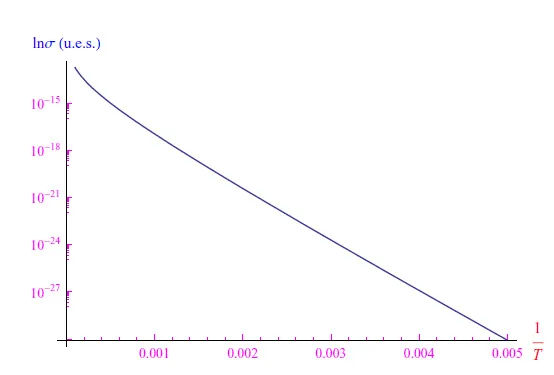
图3:本征情况下的电导率
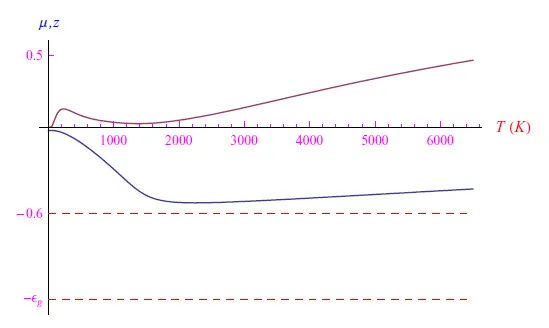
图4:Nd(0)=1磷原子(五价杂质)的化学势(蓝色曲线)和逸度随温度的变化
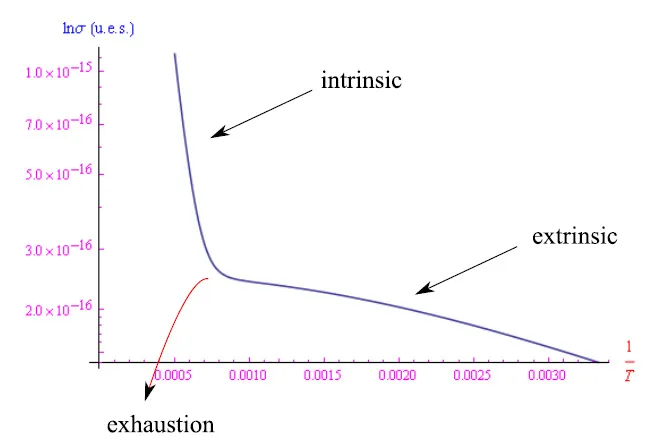
图5:非本征情况下的电导率(Nd(0)=1)
图6和图7报告了Nd(0)=100个磷原子的相同结果。最后,在图8所示的图表中,我们报告了室温(T=300K)下电导率随磷原子数量变化的趋势。
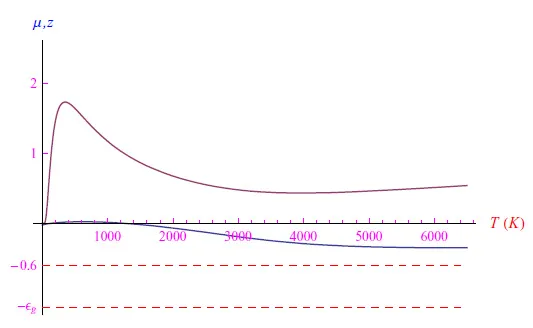
图6:Nd(0)=100个磷原子(五价杂质)的化学势(蓝色曲线)和逸度随温度的变化
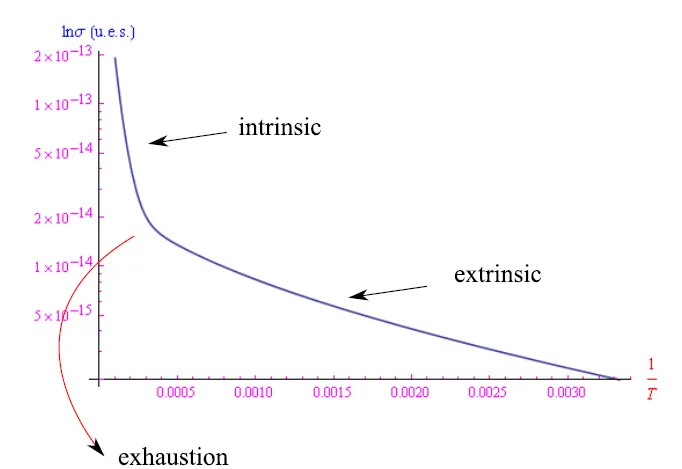
图7:非本征情况下的电导率(Nd(0)=100)
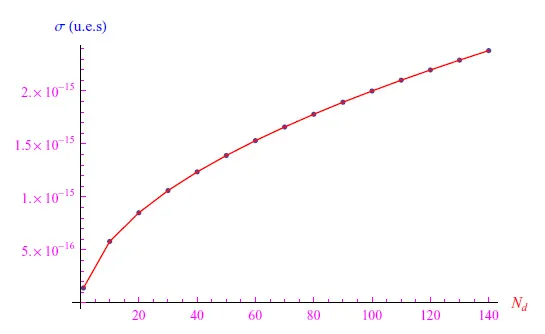
图8:电导率与掺杂原子数的关系(室温下)
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Semiconductor software package,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯