
编者注:这个由两部分组成的设计实例(DI)的第一部分展示了如何通过修改振荡器来产生有用且不寻常的脉冲发生器,第二部分也是最后一部分则会将其扩展为阶跃函数。
在本DI的第一部分中,我们了解了如何门控振荡器以生成表现良好的脉冲。现在,我们将了解如何将这个想法扩展到生成表现良好的阶跃函数或非常平滑的方波。
这里的理想函数是赫维赛德函数或单位阶跃函数,其值为0或1,且值之间有无限陡峭的过渡。正如我们在第1部分中遇到的狄拉克δ脉冲是正态分布或钟形曲线的极端情况一样,赫维赛德函数是逻辑函数(logistic function)的极限,我猜逻辑学家使用它的频率与水管工使用浴缸曲线的频率差不多。
任何使用音频设备的人都会使用方波测试,用RC时间常数来控制无穷大,这对于日常使用来说已经足够了,但另一种方法是用余弦波的一部分代替那个仍然很尖锐的阶跃。采用第1部分中的电路并添加一些门控意味着我们不是为每个触发输入生成一个完整的升余弦脉冲,而是在每个转换时获得一个半周期极性交替。其结果是:方波的频率为触发器的一半,边缘平滑。修改后的电路如图1所示。
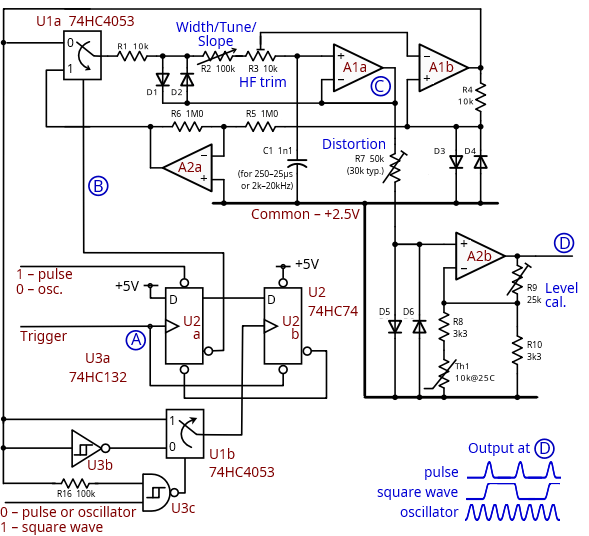
图1:在原始电路中添加的额外逻辑现在在每个触发脉冲上都会产生半余弦波,具有交替极性,从而产生具有平滑边缘的方波。
在脉冲或振荡器模式下,每当A1b的输出变为高电平时,U1b都会向U2发送复位信号,从而产生一个升余弦的完整周期。在方波模式下,每当A1b在半周期点发生变化时,U2都会复位,无论极性如何。U1b和U3b/c充当门控EXOR,通过一条支路延迟来生成复位脉冲。图2显示了一些波形,将这些波形与第1部分图2中的波形进行比较。与之前一样,当选择振荡器模式时,A2会堵塞,从而强制进行连续的正弦波操作。
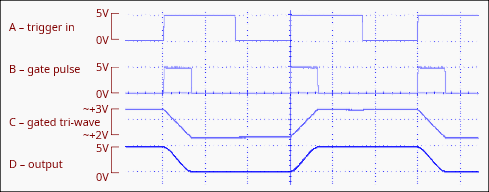
图2:图1中电路的一些波形。
图3显示了单个正向转换,并与我们的目标曲线进行比较。这些都是理论图,但实际输出非常接近余弦值。
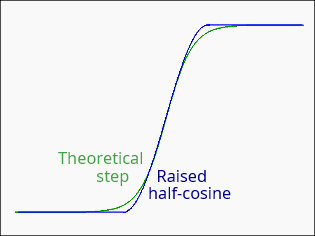
图3:目标阶跃函数是一条logistic曲线,为便于比较,显示了一段余弦曲线。
在第1部分中,我们尝试通过对三波进行一些额外的压缩来更接近正态分布曲线。这种方法在一定程度上是有效的,但过于复杂,部分原因是波形缺乏对称性。现在我们有一个对称函数可以作为目标,这应该更容易模拟。
多路复用器U1的备用部分与三个新电阻器一起提供了一个巧妙的解决方案,图4中的电路片段显示了具体的方法。
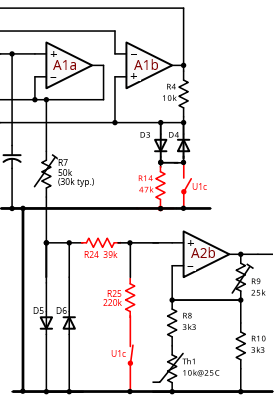
图4:添加红色组件可以更好地拟合我们的目标曲线。三波振幅增加,现在可以进一步压缩。
将47k(R14)与D3/4串联可增加跳变点的电平,因此三波现在跨度为~4.3V而不是~1.1V。通过R7增加对D5/6的驱动会导致二极管不会将三角形压缩为(余弦)正弦,而是将其压缩为更方正但幅度更大的形状。R24和R25连接在D7/8上,将二极管两端的电压降低,这样峰值(现在是平缓的曲线)就会被A2b的(轨到轨)输出裁剪。(D7/8的电阻负载略微和缓了它们的响应,这也有帮助。)
U1c有两个作用。当要生成脉冲或连续正弦波时,它使R14短路并打开R24,从而提供标准的工作条件,但在方波模式下,R14留在电路中,而R24接地,这是额外的三波幅度和压缩所需的。
波形现在看起来像图5(注意轨迹C的比例变化),而图6显示了单个实际边缘,并带有理论上理想的阶跃以供比较,并且匹配现在非常好。
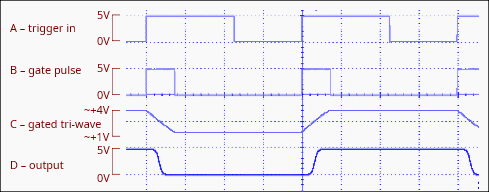
图5:添加图4所示修改后的波形。
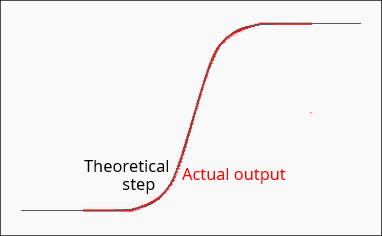
图6:目标曲线与图5中轨迹D的部分比较。
这里有一些不实的地方,图6中的两条曲线在半高点处被调整为相同的斜率。由于R24/R25将二极管两端的信号幅度降低了近12%,因此斜率也将比余弦版本小得多,但这并不是一个实际问题。
为了将所有这些变成可以进行音频测试的功能齐全的套件,我们需要添加一些额外的东西:
将所有这些放在一起,我们就得到了图7中完整且合理的最终电路。通过添加第1部分图5中详细介绍的附加组件,可以轻松容纳多个量程。也可以添加第1部分图6中所示的改进的脉冲整形电路,但可能会比较麻烦。
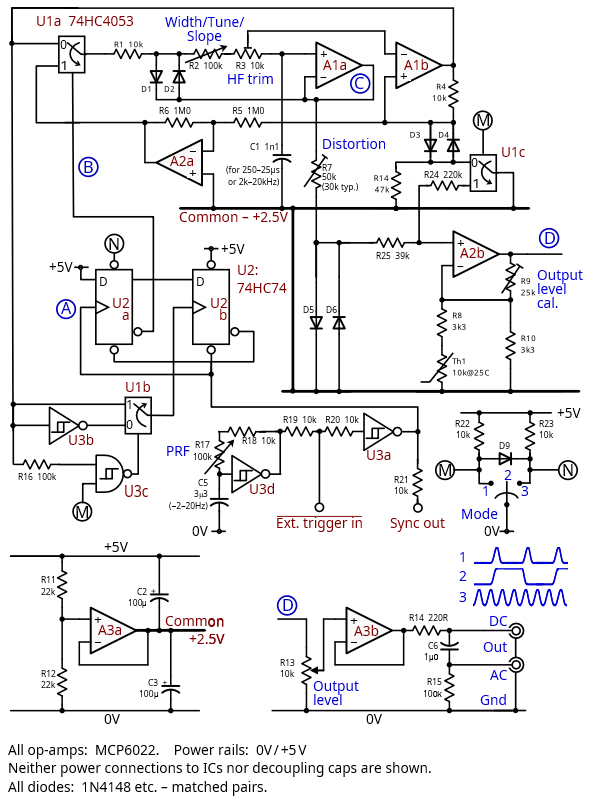
图7:完整电路现在可产生具有良好边缘形状的方波以及脉冲和连续正弦波。
没有标明引脚号是故意的,因为包含这些引脚号意味着布局已经优化。注意将逻辑信号与模拟信号分开,特别是在R24接地端及其周围,当开路时,这些接地端可能会拾取开关尖峰。U1的E-not(引脚6)和VEE(引脚7)必须为0V。
虽然这种生成良好脉冲的方法可能只是更有趣而非更准确,但它确实表明,用二极管处理三角波不仅限于生成正弦波,而这正是这个想法的起点。对于任何更复杂的情况,AWG可能是更好的解决方案,尽管它不那么有趣。
(原文刊登于EDN美国版,参考链接:How to control your impulses—part 2,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯