
在本文中,我们将研究一种一维晶体模型,该模型能够区分绝缘体的行为与金属和半导体的行为。在后者中,电导是通过隧穿过程而不是通过破坏共价键来实现的。
在Born-Oppenheimer近似(玻恩–奥本海默近似)的研究中,我们发现在任何固体(绝缘体、导体、半导体)中,电子的运动都可以与原子核(或正离子)的运动分离。在第一步近似中,我们认为原子核在各自的晶格位置上是刚性静止的。
在理想晶体中,原子核周期性地分布在三维晶格结构上,而在一维情况下,原子核则分布在一条直线上。后一种情况尽管不符合物理现实,但却是一种极好的研究工具,原因有二:1)数学形式更简单;2)可以直接推广到三维情况。
原子核正电荷的周期性分布决定了势能,该势能用周期为a的周期函数V(x)表示,后者为晶格间距。在固体物理学中,一般的周期区间[na,(n+1)a]称为晶胞,其中n为任意相对整数。
周期性无非就是“平移对称性”。众所周知,物理学中的对称性概念之所以重要,不仅因为它可以转化为与指定对称性相关的物理量的守恒,还因为它有助于寻找控制所研究物理过程的微分方程的解。在量子力学中,对称性起着更为深远的作用,例如,正如我们在之前文章中看到的,在晶格的情况下,平移对称性给出了布洛赫定理,根据该定理,“电子波”的振幅被调制,而调制包络具有晶格的周期性。这里所说的“电子波”是指能量的本征函数,即对应于指定能量的单个电子波函数。
图1显示了与原子核所在晶格位点x=na相对应的趋向于+∞的势能图。根据经典力学,单个电子被限制在指定的晶胞[na,(n+1)a]中,因为它没有足够的能量来克服无限高的势垒。从量子角度来看,我们也有类似的行为,因为与电子相关的概率波由于其无限大的值而无法跨越势垒。它为我们提供了局部信息,即与给定晶胞有关的信息,我们很容易确信它是一个驻波。根据波传播理论,我们知道相应的频率是量化的,单个电子的能级也是如此。
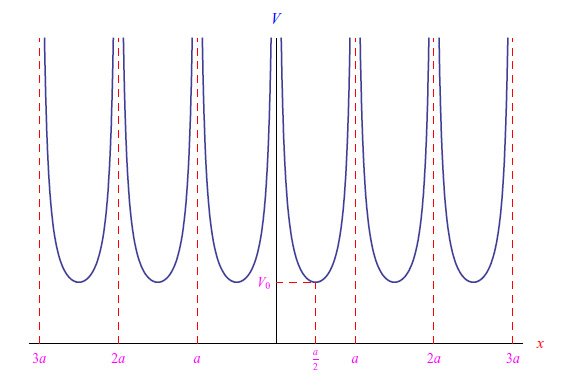
图1:表征绝缘体行为的势能V(x)
在图2中,我们报告了在势能V(x)由一系列狄拉克函数给出的特殊情况下(图3),限制在晶胞[0,a]中的电子的第二激发能级所对应的波函数趋势。选择此特定势能而不是图1中的势能对于以封闭形式(时间无关的薛定谔方程)求解相应的特征值微分方程至关重要。相比之下,图1势能的特征值方程只能进行数值积分。
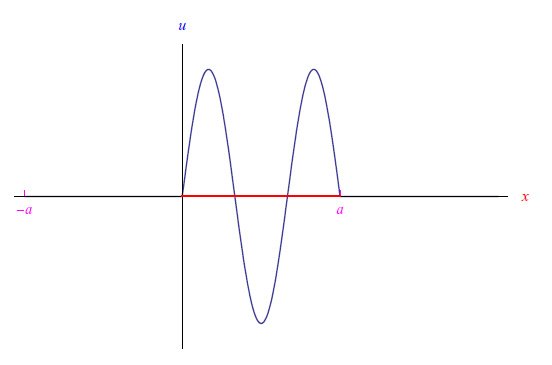
图2:受限于晶胞[0,a]中的电子所占据的第二激发能级的波函数
我们得出结论,图1中的势能模拟了一维绝缘体,因为电子与其各自的原子核牢固地结合在一起,并且即使是无限的能量也无法打破这种键。
可以通过“降低”图1中绘制的势垒来仿真一维金属的行为。然而,为了以封闭形式求解特征值方程,最好参考图3中的势垒。为此,我们将势垒定义如下:
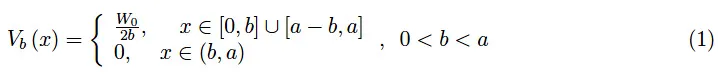
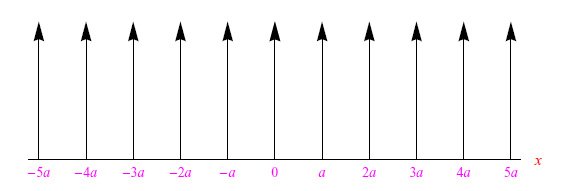
图3:实现周期势的狄拉克函数序列
实数b是一个具有长度量纲的参数,它控制势垒的高度:b→0的极限重现了图3的趋势。因此,假设b为有限值,则相当于将势垒从+∞降低到W0/2b。图4表示势能图。
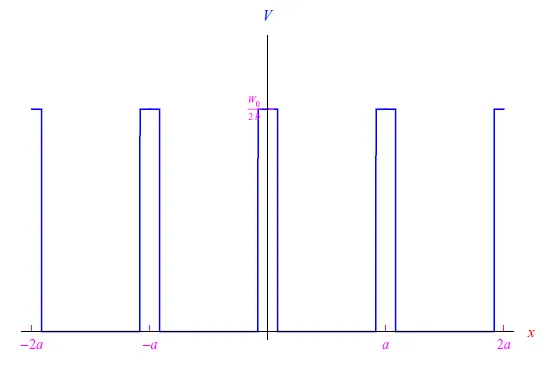
图4:势能Vb(x)
图5显示了晶胞[0,a]中的Vb(x)图。势能(1)是L. Kronig和W.G. Penney提出的模型的一种变体,用于获得金属传导的基本特征:能量值E>W0/2b对应于扩散态,对于该扩散态,布洛赫波从−∞传播到+∞,重现了金属中电子的典型行为。

图5:[0,a]中的势能Vb(x)
势能(1)还仿真了半导体和过渡金属的行为。为此,只需假设参数b的值低于金属的值即可。这相当于“提高”了势垒,因此建立了更多能量为0<E<W0/2b的束缚态。
然而,势垒不是无限高的,因此我们预计在指定晶胞[na,(n+1)a]与相邻晶胞之间发生隧穿过程。原则上,非相邻晶胞之间也可以建立该过程,然而,在所谓的紧束缚模型中,假设b的值使得仅在相邻晶胞之间建立隧穿过程。与求解势能Vb(x)的薛定谔方程相比,更好的方法是对哈密顿量的矩阵元素进行研究,如[2]所建议的那样,得到单个电子能量的表达式:

相应的图形如图6所示。在方程(2)中,量k充当布洛赫波函数的“标签”,具有多个波的量纲。量Δ>0则具有能量量纲,用于测量与绝缘体行为(无限高的势垒)的偏差。能量Er0是束缚态(Δ=0)的特征值之一,r0是相应的量子数(r0=0、1、2、…)。
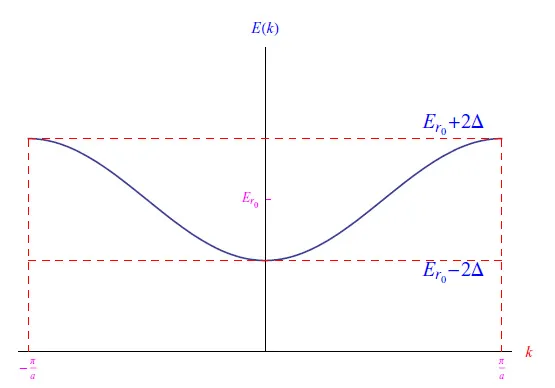
图6:E(k)的趋势
我们观察到函数E(k)是周期为2Π/a的周期函数,因此最好将其限制在区间(-Π/a, Π/a)内,在固体物理学中,该区间被称为第一布里渊区(或简称为布里渊区)。
极限Δ→0重现了b→0无限高的势垒。在紧束缚近似中,E(k)并不取决于V(x)的形状,而只取决于Δ。因此我们看到,当Δ>0时,允许的能级形成连续带[Er0−2Δ,Er0+2Δ]。于是,我们有无限个单电子态,每个态都用k标识,因此k成为一个“好量子数”。这些态根据费米-狄拉克统计量填充,众所周知,它按照泡利不相容原理重现了占据能级的热力学分布,根据该原理,每个状态k最多可以被两个具有反向平行自旋的电子占据。
一维晶体的研究不仅对于理解载流子的量子行为很有意义,而且对于“准周期”晶体的可能扩展也很有意义,对于这种晶体,通过平移破坏对称性会带来新的特性,例如所谓的拓扑绝缘体。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Semiconductors – A quantum physics toy model,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯