
1926年,意大利物理学家Enrico Fermi提出了费米子(自旋为半奇数整数倍的粒子)理想气体的统计数据(图1)。同年,英国物理学家Paul Adrien Maurice Dirac阐明了他与量子力学的联系。

图1:Enrico Fermi写给Paul Dirac的信
正如之前的文章钟所述,布洛赫定理对于研究金属或半导体中的电子动力学至关重要。不幸的是,该定理要求所研究的晶体无限延伸,这必然意味着存在同样无限数量的电荷(电子和正离子)。这种情况使得电中性条件无法用数学表达,因此,为了更好地遵循物理现实,我们必须考虑有限尺寸的晶体,然而,这破坏了正核/正离子分布的周期性,使布洛赫定理失效。
然而,可以通过调用一种称为Born-Von Karman条件(波恩-冯·卡门边界条件)的数学方法来重建周期性,在一维情况下,该条件的实现方式如下:任意指定一个自然整数N≫1,假设数量L=Na为晶体的有效长度,其中a是晶格间距,之后晶体在x轴的两个方向上被复制无数次。引入这种虚构的周期性使我们能够在有限大小但被复制无数次的晶体上进行研究,最后这个操作恢复了布洛赫定理所需的周期性。
注:或者,我们可以想象一个一维晶体,其原子核不是分布在一条直线上,而是分布在一个环上(例如,半径为R≫1的圆周),尽管其长度L有限,但由于该环可以行进无限次,并且在每条路线上我们都会发现相同的原子核分布,因此我们可以重建周期性。
在上一篇文章中,我们研究了有限高度势垒中的隧穿过程。在实现半导体/金属模型时,我们不能只考虑单个粒子,而要考虑在原子核势能场中移动的Ne个电子,该势能场由上述势垒表示。通过施加Born-Von Karman条件,我们有N个晶格位点,因此有N个原子核/离子。因此,电子数Ne与N相关,以验证电中性条件。请记住,我们处于紧束缚近似中,因此我们的模型仿真了半导体的行为。
然后,我们得到了能量随量子数k变化的趋势,该趋势确定了能量的相应特征函数(布洛赫波)。在典型的量子力学问题中,能量特征值通常用E表示,在存在大量宏观粒子的情况下,该特征值用ε表示,符号E表示总能量。结果如下:

图2绘制了相应的趋势。
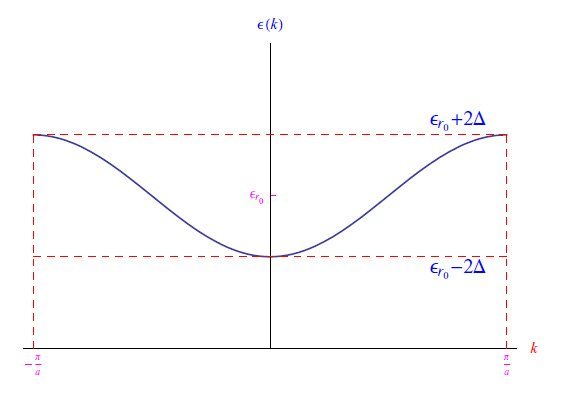
图2:ε(k)的变化趋势
我们快速回想一下,势垒高度与Δ−1成正比,其中0<Δ<εr0/2。由此可知,极限Δ→0会重现一个无限高的势垒,众所周知,该势垒不允许任何隧穿过程。因此,Δ→0重构了绝缘体的行为(在方程(1)中,εr0>0是相应束缚态下单个电子能量的特征值)。这种情况破坏了能量特征值对k的依赖性,因为从方程(1)可知ε(k)= εr0。
我们可以更直观地看到这一点,假设Δ为自由参数,然后在图2中绘制函数族ε(k),其中我们从指定的Δ>0开始,然后减小该参数,得到虚线的趋势。极限情况Δ=0以穿过(0, εr0)的水平线段表示,单个电子被限制在各自的单元中,每个单元的能量为εr0。
由于电子被分配在同样不同的单元中,因此相应的量子态在物理上是不同的。在量子力学的形式中,特征值εr0被称为简并的。简并度g是具有相同能量的(不同)量子态的数量。因此,对于Δ=0,g=+∞,因为存在无限个具有相同能量εr0的量子态。
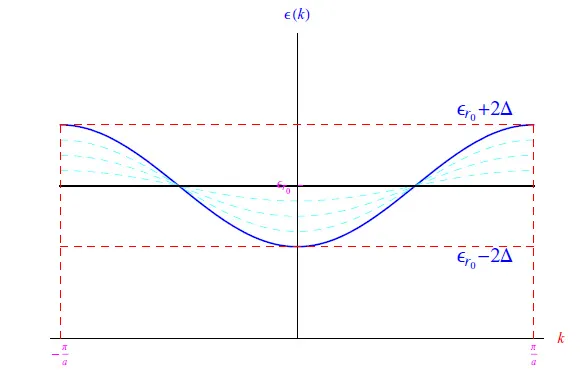
图3:ε(k)值随Δ减小的趋势
一般而言,简并性概念表征了哈密顿量具有离散特征值εi(其中i=0,1,2,…)谱的量子系统。在这种情况下,gi表示εi的简并度。在本例中,当Δ>0时,单个电子的能量呈连续分布:

因此,在连续谱的情况下,简并度gi变成函数g(ε),而g(ε)dε是ε0和ε0+dε之间的量子能态数。换句话说,g(ε)是单位能量区间内的状态数,即状态密度。在量子统计力学中,替换gi→g(ε),即从离散到连续的转变,用于那些以特征值εi极其密集的谱为特征的系统。这种替换称为连续谱近似,它有助于计算热力学量,因为无限离散特征值εi的和被dε中的积分所取代,而后者更易于操作。
为了证明上一节的结论,我们在我们的toy model中表达了电子系统的总能量:
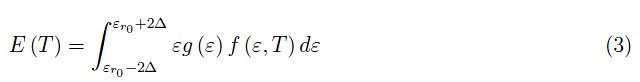
其中f(ε,T)是费米-狄拉克分布函数,正如我们已经多次看到的那样,它提供了在给定的平衡温度T下,一般能级ε>0被占据的概率:
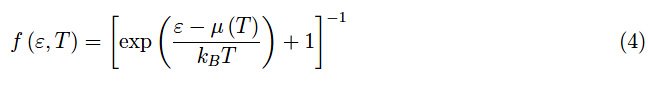
这里,µ(T)是化学势。等式(4)是费米-狄拉克统计的结果,它重现了泡利不相容原理,根据该原理,每个量子态不能被一个以上的费米子占据。在当前情况下,我们有一个电子系统,即自旋为1/2的费米子。由此可见,根据不相容原理,每一个能态e都不能被两个以上具有反向平行自旋的电子占据。单个电子的量子态除了由ε的值表征外,还取决于电子自旋的假定值。因此,对于指定的ε,我们有两个物理上不同的状态:一个自旋向上,另一个自旋向下。需要注意的是,并非范围(2)中的所有状态都被占据,因为统计分布取决于温度。
积分(3)可以写成如下形式:
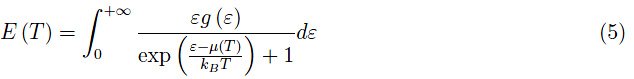
将g(ε)=0置于范围(2)之外。由于积分(5)可以进行渐近展开,黎曼Zeta函数出现在其中,因此可以对其进行有趣的解释。
为了确定所考虑模型的g(ε),最好首先将电子视为经典粒子,以计算单粒子状态的数量,然后应用量子修正。如果H(x,p)是单电子哈密顿量,则能态数≤ε为G(ε)=mis(Γ(ε)),其中Γ(ε)是相空间区域,定义为:

单个电子受到原子核力场的作用,因此具有周期性势能V(x)。由此可知,H(x,p)=(p2/2m)+V(x),且:

然而,电子的行为就像一个有效质量为m∗的自由粒子。因此,我们有:

因此,考虑到Born-Von Karman条件,我们可以写出:
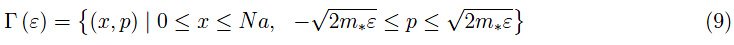
即边长为Na和2√2m∗ε的矩形:

量子修正涉及:a)考虑自旋简并因子gs=2s+1的状态计数,对于电子来说,该因子为2;b)单电子相空间的测量元素dxdp的维数,我们必须假设dxdp/h为测量元素,h为普朗克常数。
用普朗克约化常数来表示,我们有:
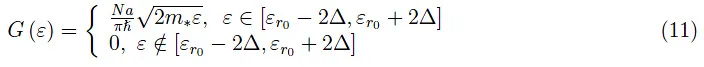
最后:
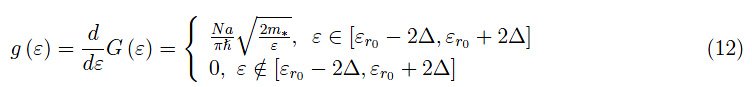
如前所述,量g(ε)对于传导电子系统的热力学量的计算至关重要。
从量子统计力学的这一基本应用出发,固态器件的诞生要得益于二十世纪上半叶物理学家们创立量子力学的努力。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Semiconductors – A quantum physics toy model (Part 2),由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯