
经常撰稿的Nick Cornford最近发表了一个非常巧妙的设计实例,使用铂RTD进行校准以输出1mV/℃信号,该信号非常适合通过标准DMM直接读出……
我认为Nick的想法太酷了,是我也想尝试拼凑出自己的版本。图1显示了最初的成果。
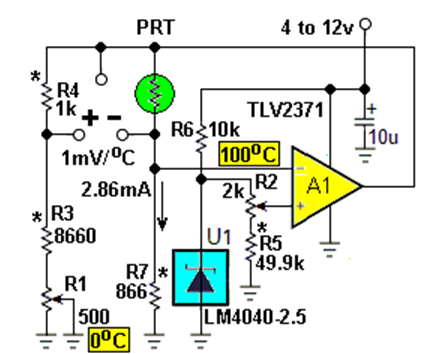
图1:PRTD电路厚颜无耻地抄袭了Nick C的想法,将普通DMM变成精密数字温度计。
图1的电路在概念上与Nick的电路相同,都是将PRT放入基本桥式拓扑中,并对PRT进行恒流激励。但在一个细节上有所不同,只有桥的PRT一半是用恒定电流主动调节的,而另一半(零点调整)只是一个无源分压器。这种方法可以稍微减少组件数量(节省了两个晶体管、一个运算放大器,也许还有一个或两个电阻器)。但这不会使电路工作得更差或更好。校准过程与Nick的DI中的程序相同,可实现其所描述的准确度。在这方面,我当然不会试图与Nick那篇写得很好的文章竞争。
事实上,我想你可能会问,如此相似的电路是否真的值得单独发布。幸运的是,这只是我们故事的开始。
由于我的电桥无源端导致PRT信号衰减了10%,为了复制Nick的1mV/℃直接读出的出色功能,我必须将PRT激励电流Iprt提高同样的10%以产生更大的信号。因此,我让Iprt=110%x1mV/℃/0.03851=2.857mA,而不是Nick在他的双恒流源电路中使用的2.597mA,到目前为止一切顺利。
但这让我开始思考Iprt的倍数再大一些会有什么影响。当然,这非常有趣,因为铂的温度系数并不完全随温度恒定,这是Callendar-Van Dusen多项式所描述的事实。它预测随着温度T的升高,铂的温度系数会从0℃值稳步下降,请注意令人讨厌的二次“B”项。
R(T) = R(0) [1 + (A T) – (B T2)]
A = 3.9083 10-3
B = 5.775 10-7
因此,我计算了电路在0℃至100℃范围内的输出,同时逐渐增加Iprt。结果绘制在图2中,X轴=实际温度,红色=读数误差(以度为单位)。
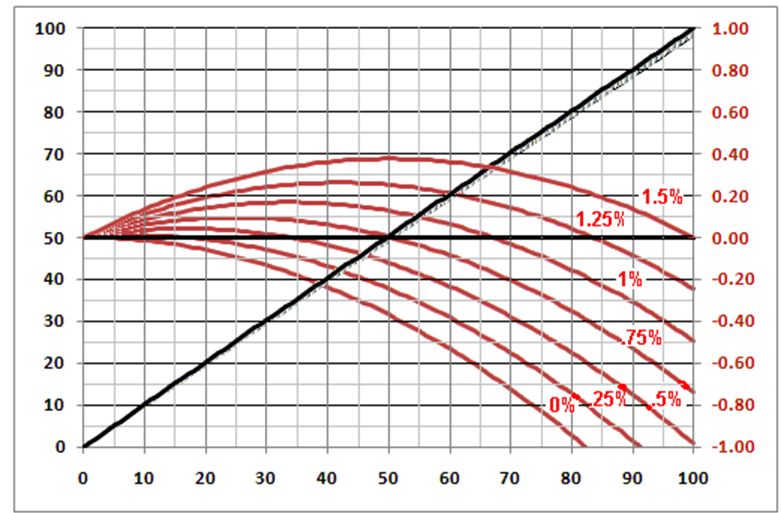
图2:这里使用的Callendar-VanDusen多项式用于预测任何给定温度下的激励电流增量,它将提供准确的读数,例如33℃时为0.5%,67℃时为1%,100℃时为1.5%。
要利用此效果连续自动修复读数,只需添加R8和R9来产生图3提供的正反馈。现在:
Iprt(T) = Iprt(0)(1 + 0.15(Vprt(T) – Vprt(0))
因此,当读出电压从0变为100mV时,Iprt激励电流将增加0至+1.5%,以准确线性化读数。图4中可以看到图3正反馈的残余误差。
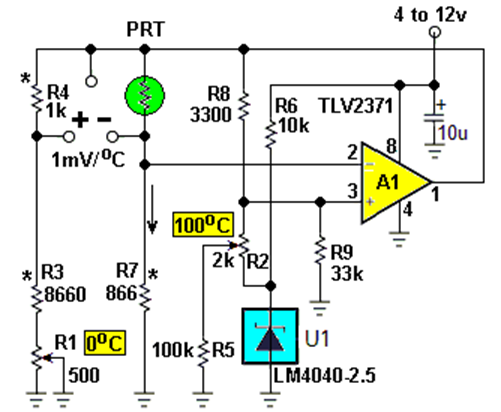
图3:通过R8到参考U1的40mV正反馈会随着温度的升高而增加PRT激励电流,从而使温度读数线性化,使温度计精确到+/-0.1℃。
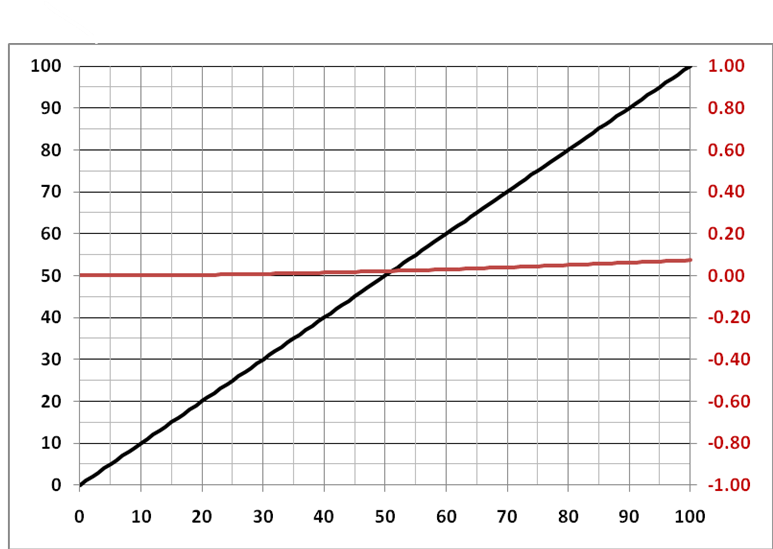
图4:图3正反馈下的残差误差。
我认为这值得单独写一篇,希望Nick也能同意。
后记:按照我的习惯,我在自己摸索出这个解决方案之后才开始研究带正反馈的PRTD线性化,但做完之后,我想看看是否有其他人在使用这种方法,是的,确实有。
猜猜是谁?我现在真的有点庆幸自己没有三思而后行,如果我已经知道Jim的电路有多复杂,我可能就不会尝试了!
(原文刊登于EDN美国版,参考链接:The power of practical positive feedback to perfect PRTDs,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯