
图1中的电路看似极其简单,但却表现出不同寻常的行为。它产生奇整数石英谐波的近似方波,包括其主频率。
您只需改变电阻器的值即可确定电路的输出频率(Fo)。

图1:一个能产生近似方波的奇整数石英谐波的简单电路。
该电路利用冲击激励来使石英产生共振振荡。与众所周知的振荡器不同,该电路探索了来自其高度非线性输出的反馈,为石英谐振器提供冲击激励,从而使电路振荡同步。
一个可能很奇怪的选择是使用施密特触发器作为有源元件,这种触发器比普通的反相器有用得多,在这种情况下,它确保了电路那不寻常的能力。
施密特触发器的输出方波仅包含奇整数谐波频率 (形式为2*π*(2*k−1)*f)。
因此,借助LPF RC滤除不良成分(参见图2中的等效电路)可以为石英提供相当好的激励。(此处C是与石英节点相关的公共电容:寄生电容加上触发输入和石英本身的电容。)
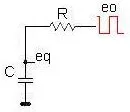
图2:为石英振荡器提供激励的LPF RC等效电路。
假设上升阈值Vt1和下降阈值Vt0是对称的(54HC14的情况),则自由运行施密特触发器RC振荡器的频率可以通过以下公式近似求得:
Fofr = 1/(2*R*C*ln2) = 0.72/ (R*C)
为了实现同步,该自由运行频率必须略低于目标频率。
注意:如果不满足此条件,电路可能会在石英的次谐波杂散组合或任何主要由RC决定的无关频率上振荡。这种振荡器的相位噪声问题也尚未解决。
该电路对于较高频率可能不太有用,因为频率越高意味着R值越低,因此该电阻对谐振器的分流就越大。较低的R值也会扭曲我们这个简单的方波振荡器模型。
但它非常适合较低的石英频率,它用于32kHz至1或2MHz的频率范围。
例如,当Fq=100kHz时,150k至250k范围内的R值对应于主频率(100kHz),85k至40k范围内的R值对应于3次谐波(300kHz),65k至75k范围内的值将对应于5次谐波(500kHz),依此类推。当然,所有这些值都是针对54HC14和Edd=5V的情况给出的指导值。
(原文刊登于EDN美国版,参考链接:Quartz oscillator with shock excitation,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯