
我们已经研究过考毕兹振荡器(Colpitts振荡器),现在我们来看一下它的好兄弟Clapp振荡器(克拉泼振荡器)。
请看图1中的图示。
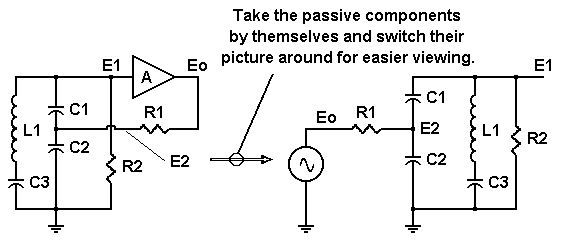
图1:克拉泼振荡器,其中无源元件排列在右侧,以便于查看。来源:John Dunn
有一个由无源元件和有源增益模块组成的RLC网络。该电路与Colpitts电路的不同之处在于使用了第三个电容器(C3)与电感(L1)串联,并且需要一条直流通路:R2接地用于增益模块。增益模块的输出阻抗为零,其增益(A)的值名义上为1,或者可能略小于1。电阻R1模拟了实际增益模块可能呈现的输出阻抗。
为了分析该电路,我们采用无源元件,将它们重新绘制为图1右侧的样子,其中G1=1/R1、G2=1/R2、S=j/(2*π*F),我们使用节点分析来推导出传递函数E1/Eo。
与Colpitts电路相比,Clapp电路的分析更为复杂,因此为了清晰起见,我在这里省略了它。不过,我在本文末尾可以看到我手写的分析笔记(不要看花了眼)。
最终结果是传递函数能以有用的形式表达,如图2所示。

图2:图1中克拉泼振荡器的传递函数的代数表达式。来源:John Dunn
注意,该方程的分母是四阶的。之所以是四阶多项式,是因为电路中有四个独立的电抗元件,L1、C1、C2和C3。
还请注意,多项式的阶数必须与电路中独立电抗元件的数量相匹配。如果我们得出其他阶数的代数表达式,那我们肯定是在某个地方犯了错误。
绘制E1/Eo与频率的比率图,我们在图3中看到了以下情况。
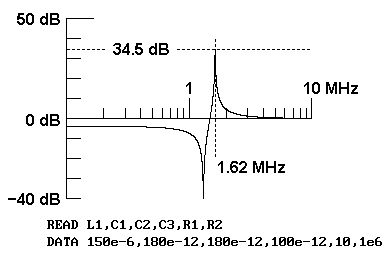
图3:代数分析得出的E1/Eo与频率的关系。来源:John Dunn
无源RLC网络的传递函数在1.62MHz频率处有一个明显的峰值,在稍低的频率处为零。当我们对该传递函数进行Spice仿真时,发现结果几乎相同(图4)。我认为这些差异是由于软件数值精度问题造成的。
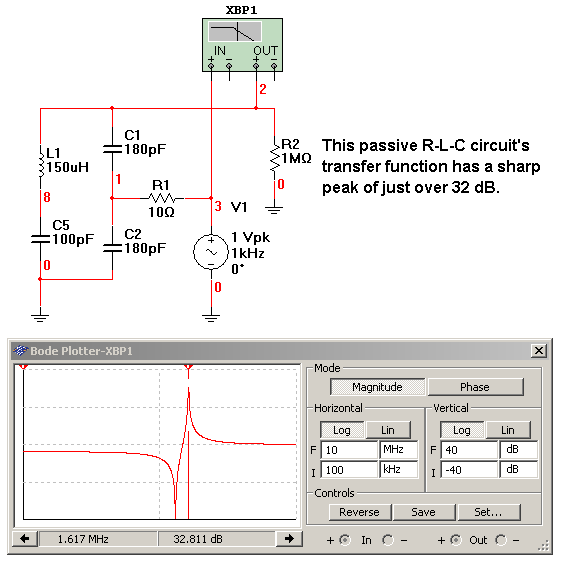
图4:SPICE分析中的E1/Eo与频率的关系。来源:John Dunn
当我们让增益模块成为电压跟随器(下例中为JFET源极跟随器)时,我们会看到传递函数峰值频率处的振荡,如图5所示。

图5:将增益模块设为电压跟随器后的Clapp振荡器仿真。来源:John Dunn
图6以手写形式显示了克拉泼振荡器传递函数的代数推导过程。
请原谅我的手写笔迹,我只是没有耐心将其打印出来。

图6:John Dunn的传递函数推导。来源:John Dunn
(原文刊登于EDN美国版,参考链接:Clapp oscillator,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯