
Edwin Henry Colpitts (1872年1月19日-1949年3月6日)
James Kilton Clapp (1897年12月3日-1965年)
上面两位天才,给我们带来了图1所示的两个经典的振荡器电路。
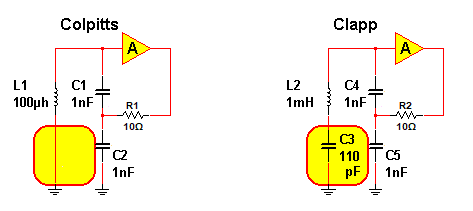
图1:两种经典振荡器电路:Colpitts(左)和Clapp(右)。
我们之前在“一起来简单聊聊考毕兹振荡器”和“再来谈谈克拉泼振荡器,和考毕兹振荡器有何不同?”中分别研究过这两个振荡器。
而对这两个振荡器进行横向对比也是十分有必要的。
Clapp振荡器是对Colpitts振荡器的改进,在上图中增加了一个电容器C3。
放大器“A”的增益值名义上是统一的,但实际上,增益值略低于统一值,因为放大器实际上是一个“跟随器”。如果使用真空管,则“A”是阴极跟随器。如果用双极晶体管,则“A”是发射极跟随器。如果用场效应晶体管,则“A”是源极跟随器。
每个振荡器的工作原理都是RLC网络在振荡频率下产生一个升压。不过,“R”不是内置组件。“R”(R1或R2)仅表示跟随器的输出阻抗。我们在这里看到的10欧姆是我随意猜测的值。其他组件也是随便选的,这些数值可便于说明这些小东西是如何工作的。
我们使用SPICE仿真来检查两个RLC网络的传递函数,如图2所示。
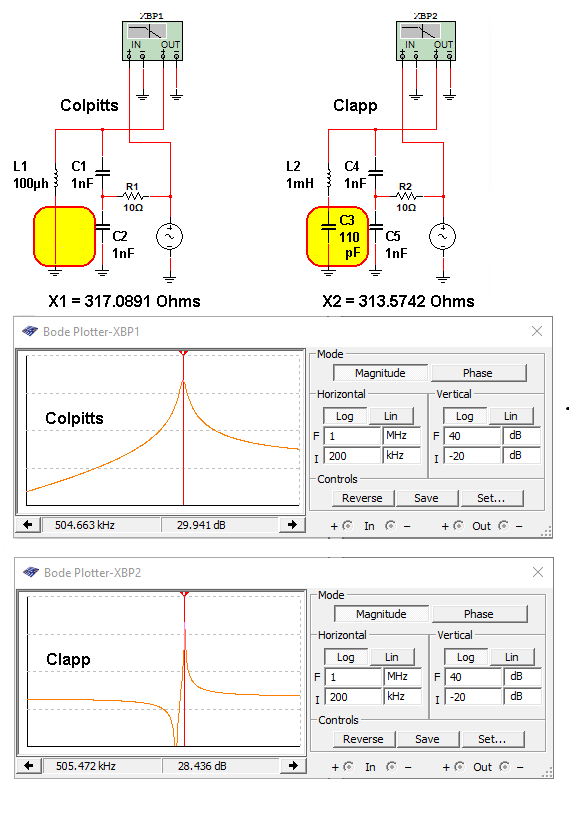
图2:使用两个RLC网络的传递函数进行Colpitts与ClappSpice仿真。
每个RLC网络的频率响应都有一个峰值,这将导致在该峰值频率处发生振荡。但是,Clapp电路的峰值比Colpitts电路的峰值更尖锐、更窄。这种变窄有利于抑制以振荡频率为中心的频谱噪声。
请注意,在上面的例子中,振荡峰值相差0.16%,L1电感器的电抗和L2 C3对的电抗相差1.12%。这只是我选择的一些比较方便的数字,目的是让两条曲线在相同的峰值频率下匹配。(我几乎成功了。)
Clapp振荡器相比Colpitts振荡器有几个优点。Clapp电路的传递函数峰值比Colpitts振荡器的传递函数峰值更窄,这往往会产生具有更少杂散频率能量的振荡器输出,这意味着信号更“干净”。
Clapp电路的另一个优点是,电容器C4和C5可以做得非常大,因为L2 C3的组合在振荡频率下看起来像是一个非常小的电感值。较大的C4和C5值意味着由“A”级输入电容的变化引起的这些电容值的任何变化对振荡频率的影响都很小。
这是因为Clapp电路的频率控制主要取决于L2 C3对的串联谐振,而不是Colpitts电路中L1与C1 C2对的并联谐振。如果“A”输入电容由于这个或那个原因而变化,Clapp电路就不太容易出现不需要的频率偏移,如图3所示。
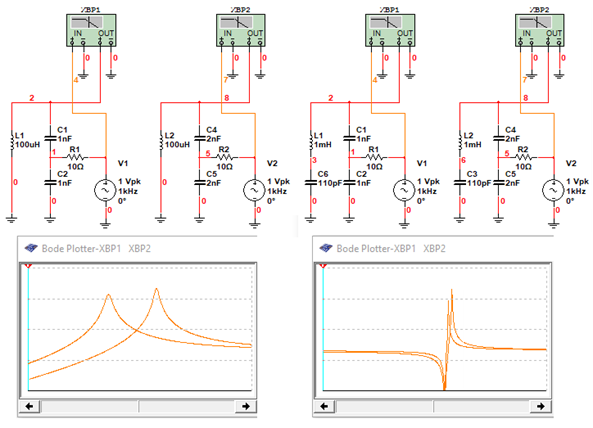
图3:Clapp电路与Colpitts电路的频率偏移比较表明,Clapp电路(右)不太容易出现这种不必要的频率偏移。
(原文刊登于EDN美国版,参考链接:Clapp versus Colpitts,由Ricardo Xie编译)
 最前沿的电子设计资讯
最前沿的电子设计资讯